Методические указания к выполнению задания 2
По пункту 1. В приведенном задании исходные данные характеризуют работоспособность сопряжения по основному параметру – зазору на различных этапах: в нормальном состоянии – начальный зазор Sн; в состоянии, допустимом без ремонта Sдр и предельном состоянии, Sпр. В качестве примера в табл.4. приведены технические условия на дефектацию сопряжения втулка – палец.
Таблица 4 – Исходные данные
| Наименование деталей сопряжения | Технические условия на сопряжение | Скорость изнашивания деталей сопряжения мм/м-ч | |||
| размеры деталей по чертежу, мм. | зазоры в сопряжении, мм. | ||||
| началь-ный Sн | допустимый без ремонта Sдр | предельный Sпр | |||
| Втулка (внутренний диаметр) | +0,038 42 +0,023 | +0,022… +0,047 | 0,11 | 0,25 | 5 ·10-5 |
| Палец (наружный диаметр) | +0,001 42 -0,009 | 2 ·10-5 |
Кроме того, в таблице 4 приведены средние скорости изнашивания деталей сопряжения по результатам эксплуатационных испытаний. В нашем случае: для втулки – Wвт = 5 ·10-5 мм/ч. и для вала (палец) – Wв = 2 ·10-5 мм/ч.
В основу расчетов положения линейная зависимость скорости изнашивания деталей (сопряжения) от наработки. Кроме того, принято, что при инженерном расчете величиной длительности приработки деталей сопряжения пренебрегают, и величина износа деталей в конце приработки не превышает величины допуска на их изготовление. Поэтому с точностью, достаточной для практических расчетов, за начальный размер детали принимают: для валов – нижний предельный размер по чертежу dmin; для отверстий – верхний предельный размер по чертежу Dmax и для сопряжения, соответственно, максимальный начальный зазор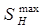 
. Методика расчета значений допустимого без ремонта Идр и предельного Ипр износов, средней скорости изнашивания Wc и полного ресурса Тcn сопряжения изложена подробно в /2/ (с 182…189).
По пункту 2. Во многих случаях разборка и сборка сопряжений с целью установления фактических износов является нецелесообразной, т.к. они снижают его полный ресурс. Поэтому для практических целей определяют полный ресурс сопряжения без микрометрических измерений. В этом случае среднюю скорость изнашивания сопряжения определяют по формулам:
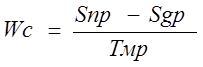, (13)
где, Sпр, Sдр – соответственно предельный и допустимый без ремонта зазоры в сопряжении, мм. В нашем случае Sпр=0,25, Sдр=0,11.
Тмр – межремонтный интервал, принятый равным Тмр=2000 ч.
Тогда: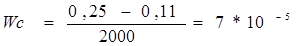 
мм/ч.
Поскольку в задании кроме полного ресурса необходимо определить допустимые без ремонта размеры деталей сопряжения, то приводятся скорости изнашивания, а средняя скорость изнашивания сопряжения может быть найдена как Wc=Wвт+Wв
Для рассматриваемого сопряжения Wc = 5 ·10-5+2 ·10-5 = 7 ·10-5 мм/ч.
Значения допустимого без ремонта и предельного износов сопряжения определяются по формулам:
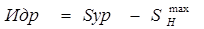, (14)
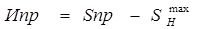(15)
составляющие формул названы выше. Для рассматриваемого примера получим:
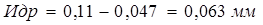
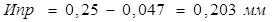
Средний полный ресурс сопряжения определяется из отношения:
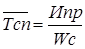(16)
который для нашего примера будет равен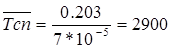 
м-ч.
К пункту 3. Принимая во внимание, что скорость изнашивания сопряжения Wc=Wвт+Wв, можно определить предельные и допустимые при ремонте размеры сопряженных деталей по следующим формулам:
для отверстия (втулки) –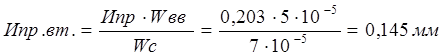 
для вала (палец) -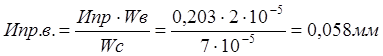 
Допустимые износы сопряженных деталей при заданном значении межремонтной наработки Тмр=2000 ч. составит:
Идр.вт=Ипр.вт. – Тмр ·Wвт=0,145 - 2000 ·5 ·10-5=0,045 мм.
Идр.в=Ипр.в. – Тмр ·Wв=0,058 - 2000 ·2 ·10-5=0,018 мм.
А допустимые без ремонта размеры деталей сопряжения определяются по следующим формулам:
для втулки - Dдр.=Dmax+Тмр ·Wвт= 42,038+2000 ·5 ·10-5=42,138 мм.
для пальца - dдр.= dmin-Тмр ·Wв= 41,991+2000 ·2 ·10-5=41,951 мм.
Где Dmax, dmin – соответственно максимальный внутренний (отверстия) и минимальный наружный (вала) диаметры сопрягаемых деталей с учетом допусков на их изготовление (размеры по чертежу).
По пункту 4. Согласно условиям задания и проведенным расчетам вычерчивается схема изнашивания деталей сопряжения в зависимости отнаработки. Образец выполнения расчетной схемы для рассматриваемогослучая приведен на рис.3.
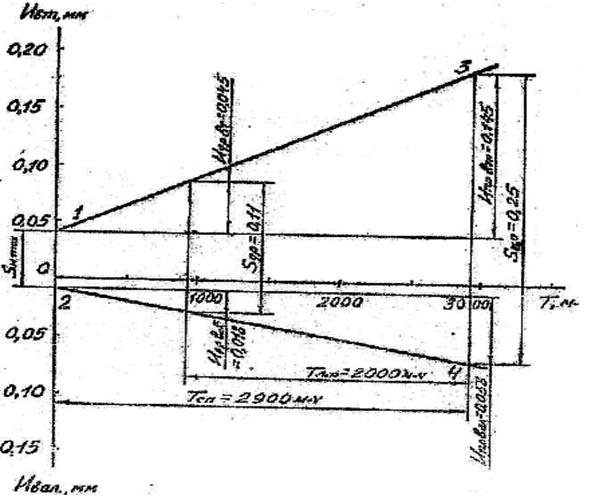
Рисунок 3 - Расчетная схема изнашивания деталей сопряжения, определения его полного ресурса, допустимых без ремонта и предельных износов сопрягаемых деталей
Вычерчивание схемы начинают с нанесения на осях координат масштабных делений, на осях ординат откладывают величины износа (вверх для втулки, вниз – для вала), а на оси абсцисс – значение наработки. Сначала откладывают значения нормального зазора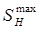 
, полного ресурса сопряжения Тсn, предельного износа для обеих деталей Ипр.в. и Ипр.вт.(см. схему). Полученные точки 1,3 и 2,4 соединяют прямыми, которые являются линиями изнашивания. Затем обозначают на схеме зазоры Sпр. и Sдр., межремонтную наработку Тмр и допустимые без ремонта износы деталей, Идр.вт. и Идр.в.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что понимают под случайной величиной? Что такое дискретная и непрерывная величины?
2. Что такое вариационный ряд? Что такое статистический ряд?
3. Что называют частотой и частостью?
4. В чем различие между опытной и теоретической вероятностями?
5. Что понимают под гистограммой и полигоном распределения?
6. Какие бывают функции распределения случайной величины?
7. Каковы абсолютные и относительные характеристики рассеивания случайной величины?
8. Способы распределения среднего значения случайной величины.
9. Охарактеризуйте закон нормального распределения.
10. Охарактеризуйте закон распределения Вейбулла.
11. Как определить доверительные границы рассеивания среднего значения показателя надежности?
12. Что такое гамма – процентный ресурс?
13. Как определяется скорость изнашивания сопряжения?
14. Какова взаимосвязь между скоростями сопряжения и деталей, входящих в сопряжение?
15. Охарактеризуйте предельный и допустимый без ремонта износ (зазор).
16. Что такое надежность?
17. Какими основными показателями характеризуется надежность?
18. Какой показатель надежности характеризует гамма – процентный ресурс?
19. Что такое безотказность?
20. Что такое долговечность?
21. Что такое зазор в сопряжении?
22. Что такое натяг в сопряжении?
Приложение А
Таблица 1 - Ресурс отверстия под подшипник коробки скоростей станка Тдр. часов (исходная информация по опытным данным)
№=70
Таблица 2
№=70
Таблица 3 - Ресурс сопряжения втулка –палец станка– Тдр. часов (исходная информация по опытным данным)
№=32
Продолжение приложения А
Таблица 4
№=32
Таблица 5
№=32
Таблица 6
№=32
Таблица 7
№=32
Продолжение приложения А
Таблица 8
№=70
Приложение Б
Варианты задания к первой задаче(предназначены для табл.1…2 прилож. 1)
| № варианта | Границы частичных интервалов, в тыс. часов | |||||
| 0,5…1,5 | 1,5…2,5 | 2,5…3,5 | 3,5…4,5 | 4,5…5,5 | ||
| 0…1,0 | 1,0…2,0 | 2,0…3,0 | 3,0…4,0 | 4,0…5,0 | 5,0…6,0 | |
| 0,7…1,5 | 1,5…2,3 | 2,3…3,1 | 3,1…3,9 | 3,9…4,7 | 4,7…5,5 | |
| 0…1,1 | 1,1…2,2 | 2,2…3,3 | 3,3…4,4 | 4,4…5,5 | ||
| 0…1,2 | 1,2…2,4 | 2,4…3,6 | 3,6…4,8 | 4,8…6,0 | ||
| 0,1…1,0 | 1,0…1,9 | 1,9…2,8 | 2,8…3,7 | 3,7…4,6 | 4,6…5,5 | |
| 0,5…1,6 | 1,6…2,7 | 2,7…3,8 | 3,8…4,9 | 4,9…6,0 | ||
| 0,5…1,4 | 1,4…2,3 | 2,3…3,2 | 3,2…4,1 | 4,1…5,0 | 5,0…5,9 | |
| 0,9…1,7 | 1,7…2,5 | 2,5…3,3 | 3,3…4,1 | 4,1…4,9 | 4,9…5,7 | |
| 0,8…1,6 | 1,6…2,4 | 2,4…3,2 | 3,2…4,0 | 4,0…4,8 | 4,8…5,6 | |
| 0,6…1,6 | 1,6…2,6 | 2,6…3,6 | 3,6…4,6 | 4,6…5,6 | ||
| 0,7…1,7 | 1,7…2,7 | 2,7…3,7 | 3,7…4,7 | 4,7…5,7 | ||
| 0,8…1,8 | 1,8…2,8 | 2,8…3,8 | 3,8…4,8 | 4,8…5,8 | ||
| 0,9…1,9 | 1,9…2,9 | 2,9…3,9 | 3,9…4,9 | 4,9…5,9 | ||
| 0,2…1,1 | 1,1…2,0 | 2,0…2,9 | 2,9…3,8 | 3,8…4,7 | 4,7…5,6 | |
| 0,3…3,2 | 1,2…2,1 | 2,1…3,0 | 3,0…3,9 | 3,9…4,8 | 4,8…5,7 | |
| 0,4…1,3 | 1,3…2,2 | 2,2…3,1 | 3,1…4,0 | 4,0…4,9 | 4,9…5,8 | |
| 0,4…1,4 | 1,4…2,4 | 2,4…3,4 | 3,4…4,4 | 4,4…5,4 | 5,4…6,4 | |
| 0,6…1,5 | 1,5…2,4 | 2,4…3,3 | 3,3…4,2 | 4,2…5,1 | 5,1…6,0 | |
| 0,2…1,3 | 1,3…2,4 | 2,4…3,5 | 3,5…4,6 | 4,6…5,1 | ||
| 0,3…1,4 | 1,4…2,5 | 2,5…3,6 | 3,6…4,7 | 4,7…5,8 | ||
| 0,4…1,5 | 1,5…2,6 | 2,6…3,7 | 3,7…4,8 | 4,8…5,9 | ||
| 0,1…1,2 | 1,2…2,3 | 2,3…3,4 | 3,4…4,5 | 4,5…5,6 | ||
| 0,1…1,1 | 1,1…2,1 | 2,1…3,1 | 3,1…4,1 | 4,1…5,1 | 5,1…6,1 | |
| 0,2…1,2 | 1,2…2,2 | 2,2…3,2 | 3,2…4,2 | 4,2…5,2 | 5,2…6,2 | |
| 0,3…1,5 | 1,5…2,7 | 2,7…3,9 | 3,9…5,1 | 5,1…6,3 | ||
| 0,6…1,7 | 1,7…2,8 | 2,8…3,9 | 3,9…5,0 | 5,0…6,1 | ||
| 0,7…1,8 | 1,8…2,9 | 2,9…4,0 | 4,0…5,1 | 5,1…6,2 | ||
| 0,7…1,6 | 1,6…2,5 | 2,5…3,4 | 3,4…4,3 | 4,3…5,2 | 5,2…6,1 | |
| 0,8…1,9 | 1,9…3,0 | 3,0…4,1 | 4,1…5,2 | 5,2…6,3 | ||
| 0,8…1,7 | 1,7…2,6 | 2,6…3,5 | 3,5…4,4 | 4,4…5,3 | 5,3…6,2 | |
| 0,9…1,8 | 1,8…2,7 | 2,7…3,6 | 3,6…4,5 | 4,5…5,4 | 5,4…6,3 |
Варианты задания к первой задаче(предназначены для табл.3…7 прилож. 1)
| № варианта | Границы частичных интервалов, в тыс. часов | |||||
| 0,6…2,1 | 2,1…3,6 | 3,6…5,1 | 5,1…6,6 | 6,6…8,1 | 8,1…9,6 | |
| 0,7…2,2 | 2,2…3,7 | 3,7…5,2 | 5,2…6,7 | 6,7…8,2 | 8,2…9,7 | |
| 0,8…2,3 | 2,3…3,8 | 3,8…5,3 | 5,3…6,8 | 6,8…8,3 | 8,3…9,8 | |
| 0,9…2,4 | 2,4…3,9 | 3,9…5,4 | 5,4…6,9 | 6,9…8,4 | 8,4…9,9 | |
| 1,0…2,5 | 2,5…4,0 | 4,0…5,5 | 5,5…7,0 | 7,0…8,5 | 8,5…10,0 | |
| 1,1…2,6 | 2,6…4,1 | 4,1…5,6 | 5,6…7,1 | 7,1…8,6 | 8,6…10,1 | |
| 1,2…2,7 | 2,7…4,2 | 4,2…5,7 | 5,7…7,2 | 7,2…8,7 | 8,7…10,2 | |
| 1,3…2,8 | 2,8…4,3 | 4,3…5,8 | 5,8…7,3 | 7,3…8,8 | 8,8…10,3 | |
| 1,4…2,9 | 2,9…4,4 | 4,4…5,9 | 5,9…7,4 | 7,4…8,9 | 8,9…10,4 | |
| 1,5…3,0 | 3,0…4,5 | 4,5…6,0 | 6,0…7,5 | 7,5…9,0 | 9,0…10,5 | |
| 0,6…2,2 | 2,2…3,8 | 3,8…5,4 | 5,4…7,0 | 7,0…8,6 | 8,6…10,2 | |
| 0,7…2,3 | 2,3…3,9 | 3,9…5,5 | 5,5…7,1 | 7,1…8,7 | 8,7…10,3 | |
| 0,8…2,4 | 2,4…4,0 | 4,0…5,6 | 5,6…7,2 | 7,2…8,8 | 8,8…10,4 | |
| 0,9…2,5 | 2,5…4,1 | 4,1…5,7 | 5,7…7,3 | 7,3…8,9 | 8,9…10,5 | |
| 1,0…2,6 | 2,6…4,2 | 4,2…5,8 | 5,8…7,4 | 7,4…9,0 | 9,0…10,6 | |
| 1,1…2,7 | 2,7…4,3 | 4,3…5,9 | 5,9…7,5 | 7,5…9,1 | 9,1…10,7 | |
| 1,2…2,8 | 2,8…4,4 | 4,4…6,0 | 6,0…7,6 | 7,6…9,2 | ||
| 1,3…2,9 | 2,9…4,5 | 4,5…6,1 | 6,1…7,7 | 7,7…9,3 | ||
| 1,4…3,0 | 3,0…4,6 | 4,6…6,2 | 6,2…7,8 | 7,8…9,4 | ||
| 1,5…3,1 | 3,1…4,7 | 4,7…6,3 | 6,3…7,9 | 7,9…9,5 | ||
| 0,6…2,3 | 2,3…4,0 | 4,0…5,7 | 5,7…7,4 | 7,4…9,1 | 9,1…9,9 | |
| 0,7…2,4 | 2,4…4,1 | 4,1…5,8 | 5,8…7,5 | 7,5…9,2 | ||
| 0,8…2,5 | 2,5…4,2 | 4,2…5,9 | 5,9…7,6 | 7,6…9,3 | ||
| 0,9…2,6 | 2,6…4,3 | 4,3…6,0 | 6,0…7,7 | 7,7…9,4 | ||
| 1,0…2,7 | 2,7…4,4 | 4,4…6,1 | 6,1…7,8 | 7,8…9,5 | ||
| 1,1…2,8 | 2,8…4,5 | 4,5…6,2 | 6,2…7,9 | 7,9…9,6 | ||
| 1,2…2,9 | 2,9…4,6 | 4,6…6,3 | 6,3…8,0 | 8,0…9,7 | ||
| 1,3…3,0 | 3,0…4,7 | 4,7…6,4 | 6,4…8,1 | 8,1…9,8 | ||
| 1,4…3,1 | 3,1…4,8 | 4,8…6,5 | 6,5…8,2 | 8,2…9,9 | ||
| 1,5…3,2 | 3,2…4,9 | 4,9…6,6 | 6,6…8,3 | 8,3…10,0 | ||
| 0,5…2,2 | 2,2…3,9 | 3,9…5,6 | 5,6…7,3 | 7,3…9,0 | 9,0…10,7 |
Продолжение приложения Б
Варианты задания к первой задаче (предназначены для табл.8 прилож. 1)
| № варианта | Границы частичных интервалов, в тыс. мотто-часов | |||||
| 0,6…2,1 | 2,1…3,6 | 3,6…5,1 | 5,1…6,6 | 6,6…8,1 | ||
| 0,7…2,2 | 2,2…3,7 | 3,7…5,2 | 5,2…6,7 | 6,7…8,2 | ||
| 0,8…2,3 | 2,3…3,8 | 3,8…5,3 | 5,3…6,8 | 6,8…8,3 | ||
| 0,9…2,4 | 2,4…3,9 | 3,9…5,4 | 5,4…6,9 | 6,9…8,4 | ||
| 1,0…2,5 | 2,5…4,0 | 4,0…5,5 | 5,5…7,0 | 7,0…8,5 | ||
| 1,1…2,6 | 2,6…4,1 | 4,1…5,6 | 5,6…7,1 | 7,1…8,6 | ||
| 1,2…2,7 | 2,7…4,2 | 4,2…5,7 | 5,7…7,2 | 7,2…8,7 | ||
| 1,3…2,8 | 2,8…4,3 | 4,3…5,8 | 5,8…7,3 | 7,3…8,8 | ||
| 1,4…2,9 | 2,9…4,4 | 4,4…5,9 | 5,9…7,4 | 7,4…8,9 | ||
| 1,5…3,0 | 3,0…4,5 | 4,5…6,0 | 6,0…7,5 | 7,5…9,0 | ||
| 0,6…2,2 | 2,2…3,8 | 3,8…5,4 | 5,4…7,0 | 7,0…8,6 | ||
| 0,7…2,3 | 2,3…3,9 | 3,9…5,5 | 5,5…7,1 | 7,1…8,7 | ||
| 0,8…2,4 | 2,4…4,0 | 4,0…5,6 | 5,6…7,2 | 7,2…8,8 | ||
| 0,9…2,5 | 2,5…4,1 | 4,1…5,7 | 5,7…7,3 | 7,3…8,9 | ||
| 1,0…2,6 | 2,6…4,2 | 4,2…5,8 | 5,8…7,4 | 7,4…9,0 | ||
| 1,1…2,7 | 2,7…4,3 | 4,3…5,9 | 5,9…7,5 | 7,5…9,1 | ||
| 1,2…2,8 | 2,8…4,4 | 4,4…6,0 | 6,0…7,6 | 7,6…9,2 | ||
| 1,3…2,9 | 2,9…4,5 | 4,5…6,1 | 6,1…7,7 | 7,7…9,3 | ||
| 0,6…2,3 | 2,3…4,0 | 4,0…5,7 | 5,7…7,4 | 7,4…9,1 | ||
| 0,7…2,4 | 2,4…4,1 | 4,1…5,8 | 5,8…7,5 | 7,5…9,2 | ||
| 0,8…2,5 | 2,5…4,2 | 4,2…5,9 | 5,9…7,6 | 7,6…9,3 | ||
| 0,9…2,6 | 2,6…4,3 | 4,3…6,0 | 6,0…7,7 | 7,7…9,4 | ||
| 0,5…2,2 | 2,2…3,9 | 3,9…5,6 | 5,6…7,3 | 7,3…9,0 | ||
| 0,6…2,4 | 2,4…4,2 | 4,2…6,0 | 6,0…7,8 | 7,8…9,6 | ||
| 0,7…2,5 | 2,5…4,3 | 4,3…6,1 | 6,1…7,9 | 7,9…9,7 | ||
| 0,8…2,6 | 2,6…4,4 | 4,4…6,2 | 6,2…8,0 | 8,0…9,8 | ||
| 0,9…2,7 | 2,6…4,5 | 4,5…6,3 | 6,3…8,1 | 8,1…9,9 |
Приложение В
Параметры и коэффициенты закона распределения Вейбулла (ЗРВ)
| В | Кв | Св | V |
| 0,80 | 1,133 | 1,428 | 1,261 |
| 0,820 | 1,114 | 1,367 | 1,227 |
| 0,840 | 1,096 | 1,331 | 1,196 |
| 0,860 | 1,080 | 1,261 | 1,167 |
| 0,88 | 1,066 | 1,214 | 1,139 |
| 0,900 | 1,052 | 1,171 | 1,113 |
Продолжение таблицы
| 0,920 | 1,040 | 1,132 | 1,088 |
| 0,940 | 1,029 | 1,095 | 1,064 |
| 0,960 | 1,018 | 1,061 | 1,042 |
| 0,980 | 1,009 | 1,029 | 1,020 |
| 1,000 | 1,000 | 1,000 | 1,000 |
| 1,040 | 0,984 | 0,947 | 0,962 |
| 1,080 | 0,971 | 0,900 | 0,927 |
| 1,120 | 0,959 | 0,858 | 0,894 |
| 1,160 | 0,949 | 0,821 | 0,865 |
| 1,200 | 0,941 | 0,787 | 0,837 |
| 1,240 | 0,933 | 0,757 | 0,811 |
| 1,280 | 0,926 | 0,729 | 0,787 |
| 1,320 | 0,921 | 0,704 | 0,765 |
| 1,360 | 0,916 | 0,681 | 0,744 |
| 1,400 | 0,911 | 0,660 | 0,724 |
| 1,420 | 0,909 | 0,650 | 0,714 |
| 1,440 | 0,908 | 0,640 | 0,705 |
| 1,460 | 0,906 | 0,631 | 0,696 |
| 1,480 | 0,904 | 0,622 | 0,687 |
| 1,500 | 0,903 | 0,613 | 0,679 |
| 1,520 | 0,901 | 0,605 | 0,671 |
| 1,540 | 0,900 | 0,597 | 0,661 |
| 1,560 | 0,899 | 0,589 | 0,655 |
| 1,580 | 0,898 | 0,581 | 0,647 |
| 1,600 | 0,897 | 0,574 | 0,640 |
| 1,620 | 0,896 | 0,567 | 0,633 |
| 1,640 | 0,895 | 0,560 | 0,626 |
| 1,660 | 0,894 | 0,553 | 0,619 |
| 1,680 | 0,893 | 0,546 | 0,612 |
| 1,700 | 0,892 | 0,540 | 0,605 |
| 1,720 | 0,892 | 0,534 | 0,599 |
| 1,740 | 0,891 | 0,528 | 0,593 |
| 1,760 | 0,890 | 0,520 | 0,587 |
| 1,780 | 0,890 | 0,517 | 0,581 |
| 1,800 | 0,889 | 0,511 | 0,575 |
| 1,820 | 0,889 | 0,506 | 0,569 |
| 1,840 | 0,888 | 0,501 | 0,564 |
| 1,860 | 0,888 | 0,496 | 0,558 |
| 1,880 | 0,888 | 0,491 | 0,553 |
| 1,900 | 0,887 | 0,486 | 0,547 |
| 1,920 | 0,887 | 0,481 | 0,542 |
| 1,940 | 0,887 | 0,476 | 0,537 |
| 1,960 | 0,887 | 0,472 | 0,532 |
| 1,980 | 0,886 | 0,468 | 0,527 |
Продолжение таблицы
| 2,000 | 0,886 | 0,463 | 0,523 |
| 2,020 | 0,886 | 0,459 | 0,518 |
| 2,040 | 0,886 | 0,455 | 0,513 |
| 2,060 | 0,886 | 0,451 | 0,509 |
| 2,080 | 0,886 | 0,447 | 0,505 |
| 2,100 | 0,886 | 0,443 | 0,500 |
| 2,120 | 0,886 | 0,439 | 0,496 |
| 2,140 | 0,886 | 0,436 | 0,492 |
| 2,160 | 0,886 | 0,432 | 0,488 |
| 2,180 | 0,886 | 0,428 | 0,484 |
| 2,200 | 0,886 | 0,425 | 0,480 |
| 2,220 | 0,886 | 0,421 | 0,476 |
| 2,240 | 0,886 | 0,418 | 0,472 |
| 2,260 | 0,886 | 0,418 | 0,472 |
| 2,280 | 0,886 | 0,412 | 0,465 |
| 2,300 | 0,886 | 0,408 | 0,461 |
| 2,320 | 0,886 | 0,405 | 0,457 |
| 2,340 | 0,886 | 0,402 | 0,454 |
| 2,360 | 0,886 | 0,399 | 0,451 |
| 2,380 | 0,886 | 0,396 | 0,447 |
| 2,400 | 0,886 | 0,393 | 0,444 |
| 2,420 | 0,887 | 0,391 | 0,441 |
| 2,440 | 0,887 | 0,388 | 0,437 |
| 2,460 | 0,887 | 0,385 | 0,434 |
| 2,480 | 0,887 | 0,382 | 0,431 |
| 2,500 | 0,887 | 0,380 | 0,426 |
| 2,520 | 0,887 | 0,377 | 0,425 |
| 2,540 | 0,888 | 0,374 | 0,422 |
| 2,560 | 0,888 | 0,372 | 0,419 |
| 2,580 | 0,888 | 0,369 | 0,415 |
| 2,600 | 0,888 | 0,367 | 0,413 |
| 2,620 | 0,888 | 0,364 | 0,410 |
| 2,640 | 0,889 | 0,362 | 0,407 |
| 2,680 | 0,889 | 0,357 | 0,402 |
| 2,700 | 0,889 | 0,355 | 0,399 |
| 2,720 | 0,889 | 0,353 | 0,397 |
| 2,740 | 0,890 | 0,351 | 0,394 |
| 2,760 | 0,890 | 0,348 | 0,392 |
| 2,780 | 0,890 | 0,346 | 0,389 |
| 2,800 | 0,890 | 0,344 | 0,387 |
| 2,820 | 0,891 | 0,342 | 0,384 |
| 2,840 | 0,891 | 0,340 | 0,382 |
| 2,860 | 0,891 | 0,338 | 0,379 |
| 2,880 | 0,891 | 0,336 | 0,377 |
Продолжение таблицы
| 2,900 | 0,892 | 0,334 | 0,375 |
| 2,920 | 0,892 | 0,332 | 0,372 |
| 2,940 | 0,892 | 0,330 | 0,370 |
| 2,960 | 0,892 | 0,328 | 0,368 |
| 2,980 | 0,893 | 0,326 | 0,366 |
| 3,000 | 0,893 | 0,325 | 0,363 |
| 3,020 | 0,893 | 0,323 | 0,361 |
| 3,040 | 0,893 | 0,321 | 0,359 |
| 3,060 | 0,894 | 0,319 | 0,357 |
| 3,080 | 0,894 | 0,317 | 0,355 |
| 3,100 | 0,894 | 0,316 | 0,353 |
| 3,120 | 0,895 | 0,314 | 0,351 |
| 3,140 | 0,895 | 0,312 | 0,349 |
| 3,160 | 0,895 | 0,310 | 0,347 |
| 3,180 | 0,895 | 0,309 | 0,345 |
| 3,200 | 0,896 | 0,307 | 0,343 |
| 3,220 | 0,896 | 0,306 | 0,341 |
| 3,240 | 0,896 | 0,304 | 0,339 |
| 3,260 | 0,896 | 0,302 | 0,337 |
| 3,280 | 0,897 | 0,301 | 0,335 |
| 3,300 | 0,897 | 0,299 | 0,334 |
| 3,320 | 0,897 | 0,298 | 0,332 |
| 3,340 | 0,898 | 0,296 | 0,330 |
Приложение Г
Функция плотности вероятностей а · f(T) закона распределения Вейбулла
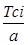 b | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 3.0 | ||||||
| 0,1 | 0,905 | 0,711 | 0,536 | 0,392 | 0,281 | 0,198 | 0,030 | ||||||
| 0,2 | 0,819 | 0,752 | 0,662 | 0,565 | 0,470 | 0,384 | 0,119 | ||||||
| 0,3 | 0,741 | 0,745 | 0,719 | 0,672 | 0,613 | 0,548 | 0,263 | ||||||
| 0,4 | 0,670 | 0,416 | 0,735 | 0,733 | 0,714 | 0,682 | 0,450 | ||||||
| 0,5 | 0,607 | 0,676 | 0,726 | 0,759 | 0,776 | 0,779 | 0,662 | ||||||
| 0,6 | 0,549 | 0,630 | 0,700 | 0,757 | 0,803 | 0,837 | 0,870 | ||||||
| 0,7 | 0,497 | 0,582 | 0,602 | 0,734 | 0,800 | 0,858 | 1,043 | ||||||
| 0,8 | 0,449 | 0,534 | 0,616 | 0,695 | 0,771 | 0,844 | 1,151 | ||||||
Продолжение таблицы
| 0,9 | 0,407 | 0,487 | 0,566 | 0,645 | 0,723 | 0,801 | 1,172 |
| 1,0 | 0,368 | 0,442 | 0,515 | 0,589 | 0,662 | 0,736 | 1,104 |
| 1,1 | 0,333 | 0,399 | 0,464 | 0,529 | 0,593 | 0,656 | 0,959 |
| 1,2 | 0,301 | 0,359 | 0,414 | 0,468 | 0,520 | 0,569 | 0,767 |
| 1,3 | 0,273 | 0,321 | 0,367 | 0,409 | 0,447 | 0,480 | 0,564 |
| 1,4 | 0,247 | 0,287 | 0,323 | 0,353 | 0,377 | 0,394 | 0,378 |
| 1,5 | 0,223 | 0,256 | 0,282 | 0,301 | 0,313 | 0,316 | 0,231 |
| 1,6 | 0,202 | 0,227 | 0,245 | 0,245 | 0,255 | 0,247 | 0,128 |
| 1,7 | 0,183 | 0,202 | 0,212 | 0,213 | 0,205 | 0,189 | 0,064 |
| 1,8 | 0,165 | 0,178 | 0,182 | 0,176 | 0,162 | 0,141 | 0,029 |
| 1,9 | 0,150 | 0,157 | 0,155 | 0.144 | 0,126 | 0,103 | 0,011 |
| 2,0 | 0,135 | 0.139 | 0,132 | 0,117 | 0,096 | 0,073 | 0,004 |
| 2,1 | 0,123 | 0,122 | 0,112 | 0,094 | 0,073 | 0,051 | 0,001 |
| 2,2 | 0,1 11 | 0,107 | 0,094 | 0,075 | 0,054 | 0,035 | - |
| 2,3 | 0,100 | 0,094 | 0,079 | 0,060 | 0,040 | 0,023 | - |
| 2,4 | 0,091 | 0,082 | 0,066 | 0,047 | 0,029 | 0,015 | - |
| 2,5 | 0,082 | 0,072 | 0,055 | 0,036 | 0,010 | 0,010 | - |
Приложение Д
Интегральная функция F (Т) закона распределения Вейбулла
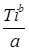 b | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,5 | 3,0 | 3,5 |
| 0,1 | 0,095 | 0,061 | 0,039 | 0,025 | 0,016 | 0,010 | 0,003 | 0,001 | 0,000 |
| 0,2 | 0,181 | 0,135 | 0,100 | 0,073 | 0,054 | 0,039 | 0,018 | 0,008 | 0,004 |
| 0,3 | 0,259 | 0,201 | 0,169 | 0,136 | 0,108 | 0,086 | 0,048 | 0,027 | 0,015 |
| 0,4 | 0,330 | 0,283 | 0,242 | 0,206 | 0,175 | 0,148 | 0,096 | 0,062 | 0,040 |
| 0,5 | 0,393 | 0,353 | 0,315 | 0,281 | 0,250 | 0,221 | 0,162 | 0,117 | 0,085 |
| 0,6 | 0,451 | 0,418 | 0,387 | 0,357 | 0,329 | 0,302 | 0,243 | 0,194 | 0,154 |
| 0,7 | 0,503 | 0,478 | 0,455 | 0,432 | 0,409 | 0,387 | 0,336 | 0,290 | 0,249 |
| 0,8 | 0,551 | 0,535 | 0,519 | 0,503 | 0,488 | 0,473 | 0,436 | 0,401 | 0,367 |
| 0,9 | 0,593 | 0,586 | 0,578 | 0,570 | 0,563 | 0,555 | 0,536 | 0,518 | 0,499 |
| 1.0 | 0,632 | 0,632 | 0,632 | 0,632 | 0,632 | 0,632 | 0,632 | 0,632 | 0,632 |
| 1,1 | 0,667 | 0,674 | 0,681 | 0,688 | 0,695 | 0,702 | 0,719 | 0,736 | 0,752 |
| 1,2 | 0,669 | 0,712 | 0,725 | 0,738 | 0,750 | 0,763 | 0,793 | 0,822 | 0,850 |
| 1,3 | 0,727 | 0,746 | 0,764 | 0,782 | 0,799 | 0,815 | 0,854 | 0,889 | 0,918 |
| 1,4 | 0,753 | 0,776 | 0,798 | 0,820 | 0,840 | 0,859 | 0,902 | 0,936 | 0,961 |
| 1,5 | 0,777 | 0,803 | 0,829 | 0,852 | 0,874 | 0,895 | 0,936 | 0,966 | 0,984 |
| 1,6 | 0,798 | 0,828 | 0,855 | 0,880 | 0,903 | 0,923 | 0,961 | 0,983 | 0,994 |
| 1,7 | 0,817 | 0,849 | 0,903 | 0,903 | 0,926 | 0,944 | 0,977 | 0,993 | 0,998 |
| 1,8 | 0,835 | 0,868 | 0,923 | 0,923 | 0,944 | 0,961 | 0,87 | 0,997 | - |
| 1,9 | 0,850 | 0,885 | 0,939 | 0,939 | 0,958 | 0,973 | 0,993 | 0,999 | - |
| 2,0 | 0,865 | 0,899 | 0,952 | 0,952 | 0,969 | 0,982 | 0,996 | - | - |
| 2,1 | 0,877 | 0,912 | 0,962 | 0,962 | 0,978 | 0,988 | 0,998 | - | - |
| 2,2 | 0,889 | 0,924 | 0,971 | 0,971 | 0,984 | 0,992 | 0,999 | - | - |
| 2,3 | 0,900 | 0,934 | 0,977 | 0,977 | 0,989 | 0,995 | - | - | - |
| 2,4 | 0,909 | 0,943 | 0,983 | 0,983 | 0,992 | 0,997 | - | - | - |
| 2,5 | 0,918 | 0,950 | 0,987 | 0,987 | 0.994 | 0,998 | - | - | - |
Приложение Е
Значение r1 и r3 для доверительных границ по Вейбуллу
| a N | 0,99 | 0,95 | 0,90 | 0,80 | ||||
| r1 | r3 | r1 | r3 | r1 | r3 | r1 | r3 | |
| 0,22 | 19,5 | 0,33 | 9,50 | 0,43 | 4,48 | 0,62 | ||
| 13,5 | 0,30 | 5,63 | 0,42 | 3,77 | 0,51 | 2,42 | 0,67 | |
| 6,88 | 0,36 | 3,66 | 0,48 | 2,73 | 0,57 | 3,95 | 0,70 | |
| 4,85 | 0,40 | 2,93 | 0,52 | 2,29 | 0,60 | 1,74 | 0,73 | |
| 3,91 | 0,43 | 2,54 | 0,55 | 2,05 | 0,62 | 1,62 | 0,75 |
Продолжение таблицы