Модель системы обслуживания с кодовым управлением множественным доступом
При моделировании систем с передачей прав по расписанию, реализуемой опросом очередей, в частности при маркерном методе управления множественным доступом, возникает серьезная проблема, вызванная тем, что получение аналитических зависимостей, связывающих время ожидания заявок с числом обращений к очередям по расписаниям,
каждое из которых требует учета затрат времени на передачу прав - сложная задача, которая не может быть решена классическими методами теории массового обслуживания [1]. Поэтому при проектировании таких систем используют некоторые приближения - аппроксимирующие функции, достаточно полный обзор которых приведен в [5, 6]. При кодовом же управлении множественным доступом в основе находится ДООП, что позволяет применить при моделировании систем известные формулы теории массового обслуживания.
В общем случае можем выделить две большие группы заявок на обслуживание - реального и нереального масштабов времени. Заявки первой группы обслуживаются по расписанию и параметром обслуживания здесь будет 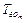 - гарантированная продолжительность обслуживания
- гарантированная продолжительность обслуживания
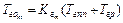 ,
,
где 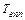 - гарантированные затраты времени на передачу прав абоненту для занятия системы ( для кодового управления при равномерном кодировании они фиксированы и составляют [
- гарантированные затраты времени на передачу прав абоненту для занятия системы ( для кодового управления при равномерном кодировании они фиксированы и составляют [  ]),
]), 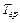 - гарантированные затраты времени при занятии ресурса, которые также, как правило, фиксированы (например, связанные с передачей 53 байтов информации в рамках сетевой технологии ATM ),
- гарантированные затраты времени при занятии ресурса, которые также, как правило, фиксированы (например, связанные с передачей 53 байтов информации в рамках сетевой технологии ATM ), 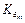 - коэффициент, задающий гарантированное предоставление ресурса (более высокий приоритет) другим абонентам системы между очередными предоставлениями прав занять ресурс m-му абоненту (приоритет абонента тем выше, чем меньше
- коэффициент, задающий гарантированное предоставление ресурса (более высокий приоритет) другим абонентам системы между очередными предоставлениями прав занять ресурс m-му абоненту (приоритет абонента тем выше, чем меньше 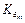 ).
).
Заявки оперативной обработки обслуживаются либо бесприоритетно, либо в режиме ОП. В последнем случае для расчета характеристик обслуживания можно воспользоваться моделью однолинейной СМО с H классами (приоритетами) очередей неограниченной длины с ординарной стратегией обслуживания заявок, образующих простейшие потоки с интенсивностями 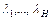 , и случайными длительностями обслуживания с известными первыми
, и случайными длительностями обслуживания с известными первыми 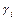 и вторыми начальными моментами
и вторыми начальными моментами 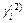 ,
, 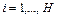 ,
, 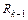 ,
, 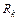 - соответственно загрузки, создаваемые различными потоками; в которой для среднего времени ожидания обслуживания заявки класса k
- соответственно загрузки, создаваемые различными потоками; в которой для среднего времени ожидания обслуживания заявки класса k 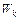 имеем [1]
имеем [1]
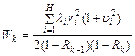 ,
, 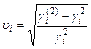
где
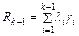 , а
, а 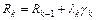 ,
,
причем т.к. 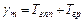 или
или 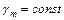 ,
, 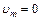 .
.
Исследуем эффективность ДОСП РМВ в альтернативных приложениях использования ОП. Эффективность использования ОП с целью защиты от перегрузок заявок реального времени, с учетом известного закона сохранения времени ожидания для ДО 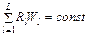 [1], где
[1], где 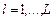 - уровни ОП,
- уровни ОП, 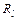 - загрузки уровней l,
- загрузки уровней l, 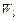 - среднее время ожидания заявок класса l, дает соответственно выигрыш для заявок РМВ - ОП 1 (для них имеем ОЦП) и проигрыш для заявок ОП 2 (пусть между собою для них также ОЦП) или ДО [(1,2,…,S ), (S +1,...,M )]
- среднее время ожидания заявок класса l, дает соответственно выигрыш для заявок РМВ - ОП 1 (для них имеем ОЦП) и проигрыш для заявок ОП 2 (пусть между собою для них также ОЦП) или ДО [(1,2,…,S ), (S +1,...,M )]
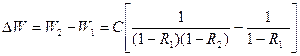 ,
, 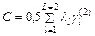 ,
,
при обработке заявок с ОП по схеме, приведенной на рис. 2.17, где в систему поступает M простейших потоков с интенсивностями 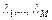 и средними длительностями обслуживания
и средними длительностями обслуживания 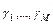 со вторыми начальными моментами
со вторыми начальными моментами 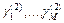 ;
; 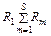 ,
, 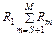 - соответственно загрузки, создаваемые потоками различных ОП ( обслуживание заявок каждого класса реализуется на основе дисциплины FIFO ). Исследуемая характеристика для случая
- соответственно загрузки, создаваемые потоками различных ОП ( обслуживание заявок каждого класса реализуется на основе дисциплины FIFO ). Исследуемая характеристика для случая 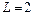 ,
, 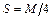 ,
, 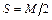 ,
, 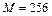 приведена на рис. 2.18, где видно, что времена ожидания заявок монотонно убывают с ростом ОП.
приведена на рис. 2.18, где видно, что времена ожидания заявок монотонно убывают с ростом ОП.
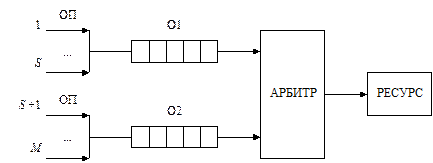
Рис. 2.17
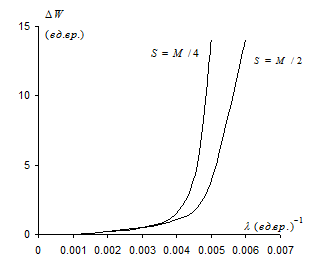
Рис. 2.18
Важной является оценка выигрыша заявок реального времени именно по параметру 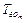 . В предположении, что такие заявки имеют бесприоритетное обслуживание, причем
. В предположении, что такие заявки имеют бесприоритетное обслуживание, причем 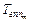 ,
, 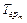 соответственно совпадают для всех M (бесприоритетное расписание) абонентов, для схемы, приведенной на рис. 2.17, имеем выигрыш, получаемый для заявок реального времени
соответственно совпадают для всех M (бесприоритетное расписание) абонентов, для схемы, приведенной на рис. 2.17, имеем выигрыш, получаемый для заявок реального времени
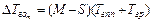
или, соответственно в относительных единицах 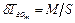 . Это говорит о том, что в предположении
. Это говорит о том, что в предположении 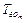 >
>  , за счет введения ОП для обслуживания заявок оперативной обработки, требования к качеству обслуживания заявок реального времени можно обеспечить с экономией производительности ресурса системы (в рассматриваемом случае – «узкого места») в
, за счет введения ОП для обслуживания заявок оперативной обработки, требования к качеству обслуживания заявок реального времени можно обеспечить с экономией производительности ресурса системы (в рассматриваемом случае – «узкого места») в 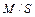 раз, причем в отличие от метода построения приоритетного расписания здесь выигрыш может быть получен и для системы реального времени с бесприоритетным обслуживанием.
раз, причем в отличие от метода построения приоритетного расписания здесь выигрыш может быть получен и для системы реального времени с бесприоритетным обслуживанием.
В предположении, что 
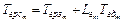 и
и 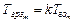 имеем
имеем 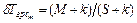 . Зависимости
. Зависимости 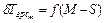 представлены на рис. 2.19, который иллюстрирует целесообразность приоритетного (в смысле ДОСП) обслуживания заявок реального времени при условиях, во-первых,
представлены на рис. 2.19, который иллюстрирует целесообразность приоритетного (в смысле ДОСП) обслуживания заявок реального времени при условиях, во-первых,  , во-вторых,
, во-вторых, 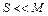 .
.
Рис. 2.19
Эффективность введения в систему внеочередных заявок ОП (как отмечалось, можно рассматривать как подход, альтернативный способу обслуживания с абсолютными приоритетами для распределенных ВС, для которых прерывание взаимодействия абонента с ресурсом связано с большими временными потерями и дополнительной сложностью децентрализованного управления доступом к ресурсу) имеет смысл оценивать мерой внеочередности их обслуживания или предоставляемым для них значением параметра 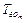 , составляющим для одной заявки ОП
, составляющим для одной заявки ОП 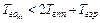 (при двух и более заявок ОП уже необходимо учитывать реализуемую для них ДО).
(при двух и более заявок ОП уже необходимо учитывать реализуемую для них ДО).
Для оценки характеристик обслуживания заявок при бесприоритетном кодовом управлении множественным доступом в рассмотренных ранее предположениях можно использовать известное выражение [1]
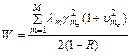 ,
, 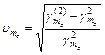
Это обусловлено тем, что в отличие от методов опроса очередей здесь отсутствует передача прав в явном виде, а 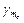 складывается из двух составляющих
складывается из двух составляющих 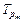 и
и 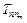 ( где в рассматриваемом случае
( где в рассматриваемом случае 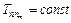 ), при этом на параметр W не сказывается несимметричность загрузки системы.
), при этом на параметр W не сказывается несимметричность загрузки системы.
Очевидно, что при реализации кодового управления множественным доступом к ресурсу, возможности повышения эффективности доступа заложены в решении задачи оптимального кодирования приоритетов абонентов системы и в выборе эффективных способов передачи прав на занятие ресурса между абонентами системы. Данным аспектам
диспетчеризации заявок при кодом управлении множественным доступом будут посвящены следующие разделы.
