Перевод целых чисел из одной системы счисления в другую

Тема: Информационные процессы в ЭВМ.

Учебныевопросы:

1. Числовая информация и системы счисления.

2. Кодирование информации.

3. Количество информации.

1.

«Всё есть число», - говорили «пифагорейцы», подчёркивая необычайно важную роль чисел в практической деятельности людей.

Известно много способов представления чисел. Но, в любом случае, число изображается символом или группой символов (словом) некоторого алфавита. Такие символы называются цифрами.

Для представления и записи чисел применялись и применяются две группы систем счисления непозиционные и позиционные.

Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, чёрточек, точек. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путём повторения одного знака, символизирующего единицу.

Древнеегипетская десятичная непозиционная система счисления.

Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. Использовались специальные знаки – иероглифы. Все остальные числа составлялись из этих ключевых при помощи операции сложения.

В непозиционных системах счисленияколичественный эквивалент каждой цифры не зависит от её положения (места, позиции) в записи числа.

Римская система счисления.

В её основе лежали знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100,500 и 1000 стали применять первые буквы соответствующих латинских слов (Centum - сто, Demimile – половина тысячи, Mile – тысяча).

Чтобы записать число, римляне разлагали его на сумму тысяч, полутысяч, сотен, полусотен, десяток, пятков, единиц. Для записи промежуточных чисел они использовали не только сложение, но и вычитание. При этом применялось следующее правило: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а поставленный слева, из него вычитается.

Например: IX – означает 9; а XI – означает 11. Десятичное число 99 запишется XCIX = -10 + 100 – 1 + 10.

Алфавитные системы счисления.

К их числу относились греческая, финикийская, славянская системы счисления, использовавшие в качестве цифр, составляющих числа, буквы алфавита соответствующего языка.

Позиционные системы счисления.

Основные достоинства любой позиционной системы счисления – простота выполнения арифметических операций и ограниченное количество символов (цифр), необходимых для записи любых чисел.

Основанием позиционной системы счисления называется возводимое в степень целое число, равное количеству цифр, используемых для изображения чисел в данной системе счисления. Основание показывает, также, во сколько раз изменяется количественное значение цифры при перемещении её на соседнюю позицию.

Возможно множество позиционных систем счисления, так как за основание системы можно принять любое число, не меньшее 2. Наименование позиционной системы счисления соответствует её основанию.

В позиционных системах счисления количественный эквивалент (значение) цифры зависит от её места (позиции) в записи числа.

В позиционной систему счисления с основанием q единицами разрядов служат последовательные степени числа q, иначе говоря, q единиц какого-то разряда образуют единицу следующего разряда.

В позиционной системе счисления число в развёрнутой форме может быть представлено в следующем виде:

Аq = ± (а_n-1 q^n-1 + а_n-2 q^n-2 + а_o q^o + а_-1 q^-1 + …а_-m q^-m) Аq = ±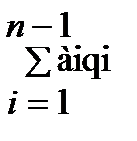

где

А – число

q – основание системы счисления

a_i– цифры алфавита данной системы счисления

n – число целых разрядов числа

m– число дробных разрядов числа

Сокращённой формой записи числа называется запись в виде

А = а_n-1 а_n-2… а₁ а_o, а _{m -1}…а_-m

Пример 1: Десятичное число А₁₀ = 4718,63.

В развёрнутой форме оно запишется: А₁₀ = 4 · 10³ + 7 · 10² + 1 · 10¹ + 8 · 10⁰ + 6 · 10^-1 + 3 · 10^-2

Пример 2: Восьмеричная система счисления. Основание: q = 8. алфавит: 0, 1, 2, 3, 4, 5, 6, 7.

Записав восьмеричное число А₈ = 7764,1 в развёрнутом виде А₈ = 7 · 8³ + 7 · 8² + 6 · 8¹ + 4 · 8⁰ + 1 · 8^-1

получим возможность выразить это число в десятеричной системе счисления

= 3584 + 448 + 48 + 4 + 0,125 = 4084,125₁₀

Перевод целых чисел из одной системы счисления в другую.

Алгоритм перевода целых чисел из системы с основанием p в систему с основанием q:

1. Основание новой системы счисления выразить числами исходной системы счисления и все последующие действия производить в исходной системе счисления.

2. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя.

3. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.

4. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.

Пример: Перевести десятичное число 173₁₀ в восьмеричную систему счисления.

Получаем: 173₁₀ = 255₈

Пример: Перевести десятичное число 173₁₀ в шестнадцатеричную систему счисления.

(D)	(А)

Получаем: 173₁₀ = AD₁₆

Иногда более удобно записать алгоритм перевода в форме таблицы.

Пример: Перевести десятичное число 363₁₀ в двоичное число.

Делимое
Делитель
Остаток

Получаем: 363₁₀ = 101101011₂