Двухступенчатые триггеры с динамической синхронизацией

Реализация композиций

Синхронных автоматов.

Реализация на триггерах элементарных автоматов Мура.

Реализуя физическую модель ЭА Мура (это ос-нова для получения композиций каноническим методом синтеза), мы будем строить схему, обеспечивающую выполнение следующих усло-вий:

1) имеются сигналы, с помощью которых на полуоси времени выделяются интервалы, соответствующие тактам, с совпадающими входными и выходными микротактами;

426,7

Только при совпадении входных и вы- ходных микротактов можно пользовать-

ся каноническим методом синтеза, пред- полагающим произвольность соедине- ний входов и выходов ЭА.

2) сигналы, определяющие значения входных воздействий Х и реакции Y ,
а также сигналы, определяющие сос- тояние автомата, не меняются во вре-
мя, отведенное такту;

3) сигналы, представляющие X, Y и S
в такте и только они задают переменные для функций переходов и выходов.

S

Q

R

В качестве основы для построения схем моделей ЭА обычно берутся триггерные схемы. Простейшая схема - асинхрон- ный RS - триггер, например,

		Q

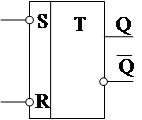
Это асинхронный автомат с Y = Q и функцией перехода Q(t+1) = F( X(t+1) , Q(t) ) вида

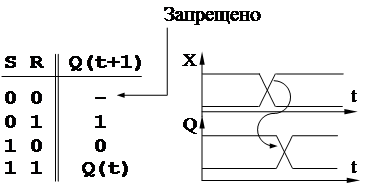Напоминание

	В асинхронных автоматах такты разделены временем смены входного воздейст-вия.

Из асинхронного получаем синхронизи-

руемый (иногда говорят синхронный)

RS-триггер (одноступенчатый).

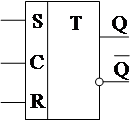Это тоже асинхронный автомат вида:

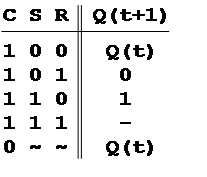При C = 1 триггер воспринимает R и S,

при C = 0 выход (состояние) сохраняется.

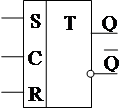
Выясним теперь, что препятствует ис- пользованию одноступенчатых синхро- низируемых RS триггеров как синхрон- ных ЭА Мура.

	C = 1 - такт ?

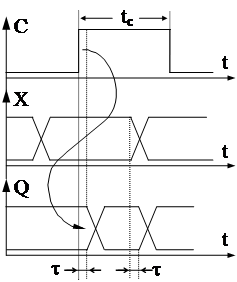1) Изменение входа при С=1 вызывает изменение Y=Q с задержкой t. Это не позволяет брать за такт время t_c>t , ибо там есть зависимость Y=F(X), а у ЭА Мура ее не должно быть.

2) Взять за такт С=1 при t_с=t нельзя,
так как t нестабильная величина, за- висящая не только от элементов схемы, но и от внешних условий их работы;

t = (t^' ¸ t").

При этом схема может в разных услови-

ях изменять или не изменять выходной

сигнал во время такта (в зависимости от величины t).

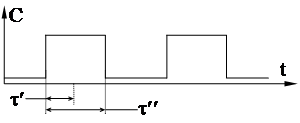4.1.1. Двухступенчатые

Триггеры со статической

Синхронизацией.

Из одноступенчатых RS - триггеров

легко построить схему, являющуюся физической моделью синхронного ЭА

Мура.

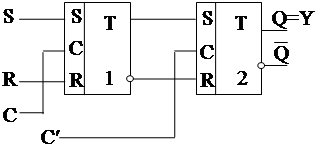
Рассмотрим модель ЭА типа RS.

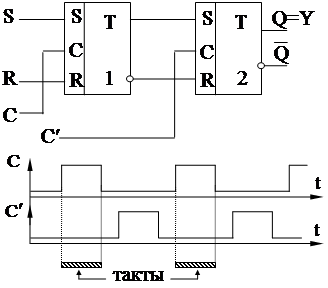
Сигналы С и С^¢ организуют тактность.

При С=1 выход и состояние Q неизмен-

ны, а входы S и R определяют Q(t+1). Неизменность входов во время такта

должна обеспечиваться внешней средой.

(t¹ и t⁰ совпадают.)

Следует отметить, что в реальных схе- мах время такта несколько больше вре- мени С=1. Входные сигналы триггера должны быть установлены до С=1 на время предустановки t_пр.

Альтернативный вариант.

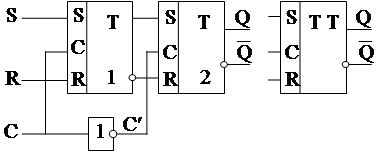Здесь все аналогично, но есть особен-

ность использования в композициях.

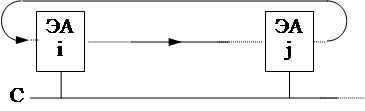
Пусть мы имеем схему с общим сигналом синхронизации

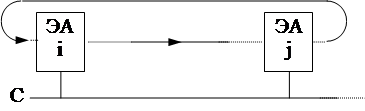Если схема "геометрически велика", то сигнал С на ЭА_i и на ЭА_j может приходить в разное время

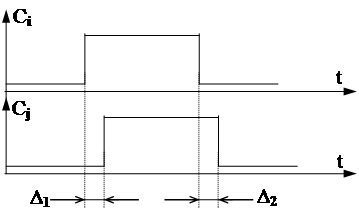Здесь во время D₁ для ЭА_i - такт и на его входах не должно быть изменений, а ЭА_j еще "имеет право" изменять выходной сигнал, а во время D₂ у ЭА_j - такт,а ЭА_i еще "имеет право" изменять выходной сигнал.

Отсюда следует, что для обеспечения правильной работы схемы нужно выпо- лнение одного из условий:

n либо задержки D₁ и D₂ столь малы, что схемы не будут успевать неправильно срабатывать;

n либо задержка D₂ совпадает по вели-чине (или очень близка) с задержкой сигналов из ЭА_i к ЭА_j ,

а D₁ - с задер-жкой выходных

сигналов от ЭА_j к ЭА_i

В исходной схеме синхросигналы С и С^¢ разделены промежутками времени, в ко-

торые могут "уложиться" возможные за-

держки D₁ и D₂ и поэтому времена тактов

и смен сигналов не пересекаются.

Из 2^х ступенчатых триггеров схем RS можно построить модель ЭА типа JK.

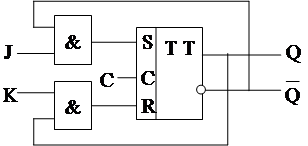Зная схему ЭА можно найти времена

такта t_т и паузы t_п схемы как модели

ЭА Мура.

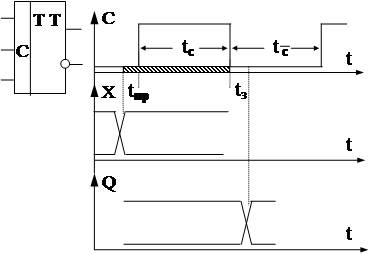Указанные времена заранее оговорены , и отсюда

t_т ³ t_пр + t_с^min

t_п ³ t_з

Следует помнить, что задержка появления Y=Q фактически лежит в интервале (0 ¸ t_з), но здесь нужно учесть максимум. Аналогично с t_пр.

Двухступенчатые триггеры с динамической синхронизацией.

Помимо схем ЭА, для которых такт вы- деляется уровнем синхросигнала, суще- ствуют схемы с выделением такта фрон- том либо спадом

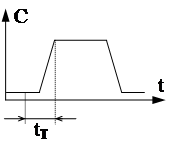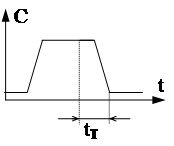Проще всего, но не экономней , получить подобную схему так

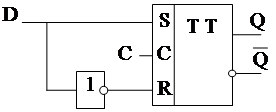Здесь Y=Q появляется после возникно-

вения С=0 и определяется значением D
в конце интервала времени С=1, так как

во входной триггер всегда идет установ-

ка ( в режиме хранения при С=1 он не

бывает).

Такую схему мы будем обозначать

При использовании данных схем из-за задержек сигнала С могут возникать пе- рекрытия времен тактов и смен сигна- лов, но с меньшим влиянием чем для схем, в которых такт определяется С=1.

Здесь "плохо" только изменение на вхо-

де ЭА_j ,происходящее во время его так-

та. Если сигнал из ЭА_i задержится в ли-

нии связи (как и С), то все будет нор-

мально.

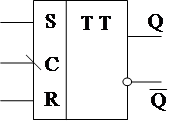Нетрудно убедиться, что на основе 2^х ступенчатых триггеров строится схема

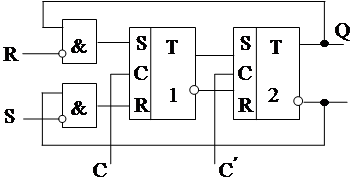(С^¢ может быть C^¢ = )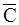

Можно было бы построить подобные схемы JK и т.д., но они оказываются сложными. Чаще всего используются, как наиболее простые, схемы построен- ные по другим принципам.

Одноступенчатые