Кодирование состояний автоматов

Решая задачу кодирования состояний,

мы будем полагать, что кодирование

входного и выходного алфавитов зада-

но, хотя в принципе это не обязательно,

так как подобная ситуация чаще всего встречается на практике.

Разные варианты кодирования состоя- ний автомата позволяют получать схе- мы, разные по:

1) сложности КС, реализующих функции возбуждения и выхо-

дов;

2) возможности сохранения работо-способности схемы отдельных ее элементов (отказоустойчивости);

3) надежности работы в условиях

возможных рассогласований времен тактов ЭА.

Здесь обсуждается кодирование, упрощаю-

щее КС автомата.

Рассмотрим автомат вида:

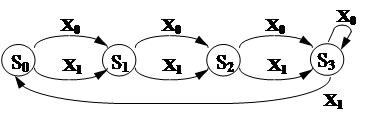(Функцию выходов не рассматриваем.)

Займемся структурным синтезом этого автомата.

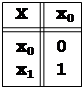
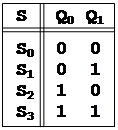Фиксируем коды алфавитов:

Примем, что ЭА - типа Д

и построим кодированную

таблицу переходов и возбуждения ЭА.

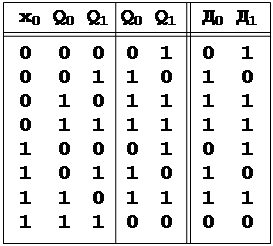По таблице можно получить Д ₀ и Д ₁ в виде МДНФ

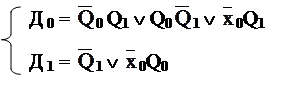При малом числе переменных миними- зировать удобно по карте Карно.

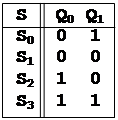Закодировав состояния, как

и построив новую кодирован-

ную таблицу переходов и воз-

буждения ЭА, мы получим но-

вые Д ₀ и Д ₁ :

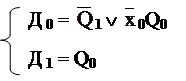Новый вариант кодирования дал функ- ции возбуждения, реализация которых заметно проще.

Наша цель - искать кодирования состояний, дающие простые схемы.

Наибольшая простота достигается, если

в результате кодирования получаются

функции, каждая (или значительная

часть) из которых не зависят от некото-

рых переменных, являющихся аргумен-

тами функций переходов и выходов.

В рассмотренном примере получено

Д ₁ = Q₀ ,

хотя в общем виде

Д ₁ = f(x₀,Q₀,Q₁).

Здесь кодирование привело к несущес- твенной зависимости Д ₁ от Х₀и Q₁.

На практике обычно используют:

1) методы, основывающиеся на знании семантики функций переходов;

2) эвристические методы, учитывающие локальные характеристики связности отдельных состояний ;

3) Методы, учитывающие взаимосвязь функций переходов и выходов.

Мы будем рассматривать 2) и 3) .

Начнем с 2) .

Простейший алгоритм кодирования для

ЭА типа Д.

1. Определяется число ЭА как log ₂ числа состояний автомата.

2. Состояния автомата упорядочи-ваются по убыванию числа пере-ходов в них.

3. Коды состояний ЭА упорядочи-ваются по возростанию числа еди-

ниц в кодах.

4. Состояниям с большим числом переходов в них ставятся в соот-ветствие коды с меньшим числом единиц.

В вышеприведенном примере получаем

Такое кодирование даст

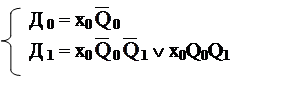Результат проще 1-го варианта, но сложнее 2-го.

Алгоритм, минимизирующий числоизменений состояний ЭА.

Обозначим W =å t_mp , где t_mp - число ЭА, изменяющих свое состояние при перехо-

де из S_m в S_p и из S_p в S_m . Суммирование

ведется по всем переходам (дугам) авто-

мата.

W может служить оценкой сложности КС автомата, раализующей функции возбуждения: чем меньше W тем проще КС.

Экспериментально-статистическая про- верка подтверждает эту гипотезу.

Алгоритм

1. Состояние, в которое идет наи-большее число переходов, коди-

руется 00...00.

2. Отыскивается состояние, наибо-

лее связанное по числу переходов

с ранее закодированными состоя-

ниями, и кодируется так, что бы

получить min текущего значения W.

3. Процедура заканчивается после кодирования всех состояний.

При малом числе состояний удобно пользоваться грфом автомата, при большом - таблицей переходов.

Пример.

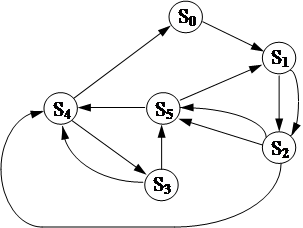
1. S₄ Û 000.

2. S₃ Û 001.
t₃₄ =2.

3.

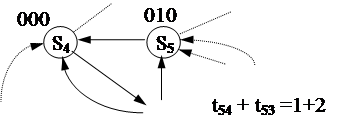191

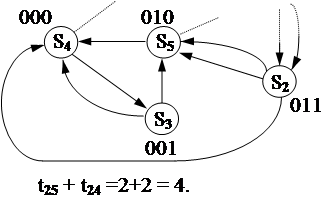4.

Взяв, например, код 100 получим t₂₅ + t₂₄ =4+1=5.

Завершая, получим:

5. S₁ Û 111.

6. S₀ Û 100.

Вариант не единственный и, возможно,не лучший, так как минимизация выполняется локально.

Учет взаимосвязи функций переходов ивыходов.

А. Автоматы Мура

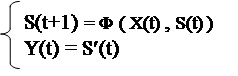Идея в построении схемы, реализующей

При S = S¢ | S¢¢ .

Схему можно рассматривать как модер-

низацию канонической реализации с от-сутствующей (тривиальной) КС функций выходов.

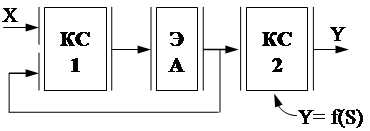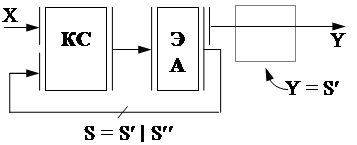Выгода обуславливается:

¨ малой стоимостью ЭА, число которых обычно растет;

¨ использованием реализации функциональных зависимостей S¢(t+1)=Ф(X(t) , S(t) ) для реализации и Y, и функций возбуждения ЭА.

Алгоритм кодирования будем рассматривать на примере автомата :

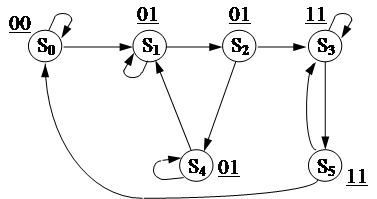Алгоритм.

1.По значениям функций выходов, отмечающим состояния, фиксируем коды S¢ для каждого состояния S.

Пример

S₀¢= 00 ; S₁¢= 01 ; S₂¢= 01 ;

S₃¢= 11 ; S₄¢= 01 ; S₅¢= 11 ;

2. Выделяем подмножества состояний, не-различимых по коду S¢, и определяем наибольшее число состояний, имеющих одинаковый код.

Пример

Подмножества: (S₁ , S₂ , S₄);( S₃ , S₅)

Наибольшее число неразличимых по

коду S¢ состояний - 3.

Примечание

Если в автомате есть состояния с неопре- деленными значениями выходов, то они доопределяются и относятся к выделен- ным подмножествам так чтобы:

1) по возможности использовать коды S¢ , которые еще не были использованы;

2) не увеличивать наибольшее число состояний, имеющих одинаковый код.

3. Если все состояния различимы по коду S¢ , кодирование закончено, причем S = S¢ .

В рассматриваемом примере кодирование не закончено.

4. Определяем разрядность кода S¢¢ как log₂ от наибольшего числа неразличимых по коду S¢ состояний.

В нашем примере имеем разрядность , равную log ₂ 3 = 2.

5. Кодируем состояния S= S¢ | S¢¢ (с учетом того, что значения S¢ уже зафик-сированы) по одному из алгоритмов кодирования состоя-ний, не учитывающих взаимо-связи функций выходов и пере-

ходов.

В примере будем использовать алгоритм, минимизирующий число изменений сос-

тояний ЭА, что даст:

1) S₀ = 0000 4) S₄ = 0110

2) S₁ = 0100 5) S₃ = 1101

3) S₂ = 0101 6) S₅ = 1100

Схема будет иметь вид:

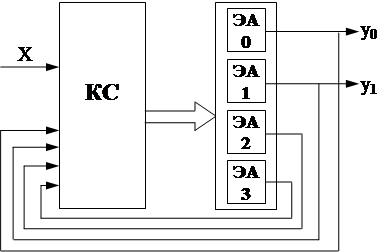
Б. Автоматы Мили.

Здесь Y=F(X,S) , а не F(S) как у автома- тов Мура. Поэтому упрощение схем обы- чно не удается получить.

Замечания о применимости метода кодирования.

1. Использование для кодов состояний авто-матов Мура или Мили значений Y ведет к увеличению разрядности кода S (числа пе-ременных функций возбуждения и выходов).

В этом случае реализация КС автомата на

базе БИС ПЗУ может оказаться невыгод-

ной, так как сложность таких КС сильно

зависит от числа переменных.

В других случаях, и в том числе для КС
на БИС ПЛМ , рассматриваемый метод кодирования состояний автоматов Мура

(реже Мили) обычно дает хорошие резу-

льтаты.

2. Использование Y для представления

кодов состояний может оказаться неце-лесообразным при (log₂k) << m, где k –

число состояний автомата, а m - число

выходов.

При этом не используют Y для предста-

вления кодов состояний, либо использу-

ют только m¢ из m выходов Y , как будто

других выходов нет. Обычно это выходы

при использовании которых разрядность

S¢¢ будет заметно меньше чем log₂k, а разрядность S¢ близка к log₂k.

В результате получается схема вида:

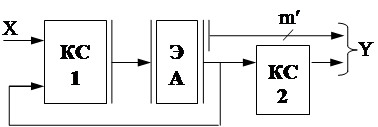Выбор ЭА.

Сложность КС автомата зависит от того, какие типы ЭА используются в автомате, так как для разных ЭА требуются разные функции возбуждения.

Оптимальный выбор ЭА связан с пере-

бором большого числа вариантов схем.

Задача усложняется тем, что в общем

случае выбор ЭА следует совмещать с

выбором кодов состояний.

Приближенное решение задачи выбора

ЭА можно проводить на основе локаль-

ного независимого подбора типов отдель-

ных ЭА из числа перебираемых.

Просмотрев ЭА_i для i = 0 ¸ k-1, выберем набор ЭА.

Рассматривая ЭА_i нужно для каждого ти-

па ЭА_i : D, T, JK, и т.д. получить функции возбуждения и выбрать тип ЭА, требую-

щий наиболее простую КС.

Оценка сложности КС может получаться

по разному в зависимости от используе-

мых ЛЭ.

Можно строить прототип КС, используя

простые приемы синтеза; можно оценивать

по числу конъюнкций в ДНФ; можно оце-

нивать по числу переменных и т.п.

Следует отметить, что на практике вы- бор из l типов ЭА часто связан с целе- сообразностью использования одного типа всех k ЭА. При этом перебор сок- ратится с k´l до l вариантов.

В некоторых случаях выбор типов ЭА

обуславливается соображениями, не свя-занными со сложностью КС автомата, на-пример, со сравнительными характерис-

тиками отдельных типов ЭА: надежность, потребляемая мощность и т.д.