Характеристики трафика
2.1. Уровни анализа трафика в мультисервисных сетях
Потоки заявок на использование канального ресурса образуют трафик мультисервисных сетей. В зависимости от принятой модели, в качестве заявок могут рассматриваться события поступления отдельных пакетов, поступление групп пакетов, объединенных в кадры, заявки на установление соединения.
Рассмотренная на примере сети АТМ [9] иерархия временных уровней анализа информационных потоков, схематично показана на рис. 2.1. Приведенные обозначения имеют следующий смысл:
Тн – длительность соединения,
Тi – длительность интервала времени между отдельными соединениями,
Тs – длительность интервала времени отсутствия поступления ячеек,
Тв – длительность интервала сгущения поступления ячеек,
Та – длительность интервала времени между последовательными поступлениями ячеек,
Тс – длительность интервала времени передачи ячеек.
Длительности интервалов времени между событиями на каждом из уровней различаются на несколько порядков. Например, в случае передачи речи с использованием технологии АТМ, длительность соединения обычно измеряется сотнями секунд, длительность интервала сгущения в поступлении ячеек имеет порядок сотен миллисекунд, а время передачи ячеек при скоростях несколько сотен мегабит в секунду уже имеет порядок единиц микросекунд.
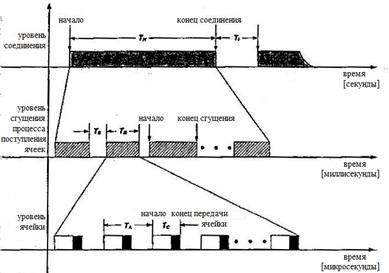 |
| Рис. 2.1 Иерархия детальности анализа информационных потоков в сетях на базе передачи технологии АТМ |
На уровне пакетов поступающая информация представляет собой дискретный поток, порождаемый каждым из источников с интенсивностью на несколько порядков меньше, чем скорость используемой для передачи цифровой линии. На этом уровне большинство источников информации порождают локально периодический поток. За периодом генерации пакетов, обычно происходящим с максимальной для рассматриваемого источника скоростью, следует период времени, когда пакеты не поступают.
Типичная задача, которая решается на уровне анализа поведения пакетов, связана с оценкой размеров буфера при мультиплексировании нескольких входных потоков. Соответствующая модель АТМ – мультиплексора схематично показана на рис. 2.2.
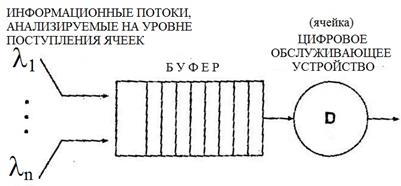 |
| Рис. 2.2 Схема модели телетрафика, используемая для оценки размеров буфера при анализе процессов мультиплексирования информационных потоков, рассматриваемых на уровне поступления ячеек |
2.2. Основные параметры пакетного трафика
Будем считать, что процесс передачи информации продолжается в течение некоторого отрезка Т. это может быть сеанс телефонного разговора, сессия видеоконференции или передача данных от ЭВМ. Передача информации является статистическим процессом. При пакетной передаче основной характеристикой трафика служит скорость передачи B(t)[бит/с][9].
Различают:
| пиковую скорость: | 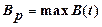 |
| среднюю скорость: | 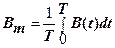 |
| эффективную скорость: | 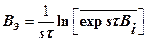 , , |
где Bi - скорость при i измерении на интервале 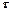 . Если скорость Bi=B постоянная, то BЭ=B [бит/с].
. Если скорость Bi=B постоянная, то BЭ=B [бит/с].
Соотношение между пиковой и средней скоростями называют коэффициентом пачечности (2.1)
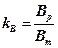 , , | (2.1) |
где Bр - пиковая скорость (см. рис.2.3).
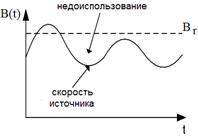 | 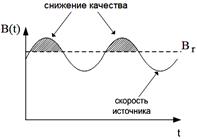 |
| Рис. 2.3 Изменение скорости передачи B(t) |
Пакетный трафик, на примере передачи ячеек АТМ, характеризуется следующими параметрами:
- пиковая скорость (PCR- Peak Cell Rate), измеряемая числом ячеек, генерируемых источником за единицу времени ( секунду)
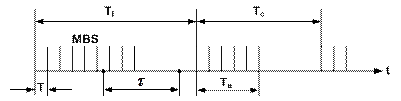
- поддерживаемая скорость (SCR – Sustainable Cell Rate), которая является скоростью передачи пачки ячеек максимального размера за максимальный интервал времени между началами соседних точек 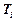 . SCR=MBS/Ti
. SCR=MBS/Ti
- максимальный размер длины пачки, измеряемый в числе ячеек (MBC – Maximum Burst Size)
- интервал между смежными ячейками Т [с]
Очевидно, что SCR=MBS/T [яч/с], а PCR= 1/T [яч/с]
- максимальная длительность пачки TB=(MBS-1)T [с].
Указанные параметры, характеризующие основные свойства пакетного трафика, показан на рис.2.4.
 |
| Рис. 2.4 Параметры пакетного трафика |
Величины Тв и Тс являются случайными и характеризуются соответствующими распределениями вероятностей.
Средняя интенсивность передачи ячеек l определяется соотношением
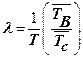
Где 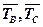 - математические ожидания.
- математические ожидания.
2.3. Распределения вероятностей
Пакетный трафик может рассматриваться как случайный процесс, представляющий поток заявок. Интервалы Ji между соседними заявками являются случайной величиной. Плотность распределения вероятностей указанных интервалов W(Ji) для стационарного процесса не зависит от времени. Функция распределения вероятностей (2.2) представляет собой интеграл (2.3)
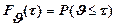 | (2.2) |
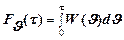 | (2.3) |
В соответствии с законом распределения вероятностей, для случайной величины Ji могут быть определенно математическое ожидание 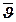 , второй начальный момент
, второй начальный момент 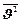 и дисперсия DJ. Однако, случайный процесс заявок может также быть характеризован интенсивностью поступления заявок в любой момент времени l(t) [заявок/с].
и дисперсия DJ. Однако, случайный процесс заявок может также быть характеризован интенсивностью поступления заявок в любой момент времени l(t) [заявок/с].
Плотность распределения вероятностей указанной случайной величины 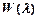 для стационарного процесса не зависит от времени, а функция распределения вероятностей (2.4) представляет собой интеграл (2.5).
для стационарного процесса не зависит от времени, а функция распределения вероятностей (2.4) представляет собой интеграл (2.5).
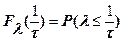 | (2.4) |
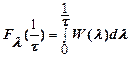 . . | (2.5) |
В соответствии с законом распределения вероятностей для случайной величины l(t) могут быть определены математическое ожидание, второй начальный момент и дисперсия.
С величиной интенсивности l(t) непосредственно связана случайная величина mi(t), представляющая число заявок, поступающих в течение интервала времени t, непосредственно следующего за моментом времени ti
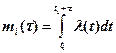 [заявок], [заявок], 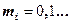 | (2.6) |
Для указанной случайной величины также могут быть определены распределение вероятностей, математическое ожидание 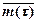 , второй начальный момент
, второй начальный момент 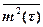 и дисперсия Dm(t). Для стационарного процесса указанные величины не зависят от моментов времени ti, в которые начинается отсчет интервала t.
и дисперсия Dm(t). Для стационарного процесса указанные величины не зависят от моментов времени ti, в которые начинается отсчет интервала t.
Для простейшего потока, в котором интервалы между заявками распределены экспоненциально, вероятности P(mi) подчиняются закону Пуассона.
2.4. Взаимные корреляционные моменты
Теперь, разделим весь рассматриваемый интервал времени 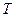 на
на 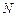 одинаковых интервалов, длительностью t. Порядковый номер интервалов обозначим через i. Вследствие ординарности потоков заявок, в течение каждого i-го интервала времени поступает целое число заявок mi(t) (
одинаковых интервалов, длительностью t. Порядковый номер интервалов обозначим через i. Вследствие ординарности потоков заявок, в течение каждого i-го интервала времени поступает целое число заявок mi(t) ( 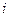 =0,1,2…). Число заявок, поступающих в течение времени
=0,1,2…). Число заявок, поступающих в течение времени 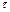 , является дискретной случайной величиной с математическим ожиданием
, является дискретной случайной величиной с математическим ожиданием 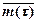 , вторым начальным моментом
, вторым начальным моментом 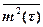 и дисперсией Dm(t).
и дисперсией Dm(t).
Допустим, что в течение каждого i-го интервала времени в системе массового обслуживания (СМО) находится qi(t) заявок, ожидающих в очереди. Длина очереди также является дискретной случайной величиной с математическим ожиданием 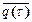 .
.
Обозначим через qi-j(t) элемент последовательности случайных чисел, сдвинутый влево относительно qi(t) на j промежутков времени t.
Определим вторые взаимные начальные моменты последовательностей mi(t) и qi-j(t), как математические ожидания произведений их соответствующих элементов.
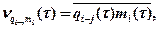 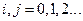 | (2.7) |
Вторые взаимные центральные моменты указанных последовательностей, называемые корреляционными моментами или ковариацией, определяются, как математические ожидания произведений центрированных значений их элементов.
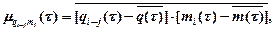 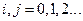 | (2.8) |
Между указанными моментами существует известное соотношение
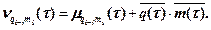 | (2.9) |
В дальнейшем, мы покажем, что взаимные корреляционные связи оказывают существенное влияние на размеры очередей.
