Методы теории игр в экономике. Решение игры двух лиц с нулевой суммой в смешанных стратегиях

Игра – упрощённая матричная модель конфликтной ситуации, которая ведётся по определенным правилам. Исход игры - значение некоторой функции, называемой функцией выигрыша (платёжной матрицей), которая может задаваться либо аналитическим выражением, либо таблично (матрицей). Стратегия – сов-ть правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации.

Игра в чистых стратегиях – без вероятностей. В таких играх сначала находится максимин (нижняя чистая цена, минимальный выигрыш игрока А), потом минимакс (верхняя чистая цена, максимальный проигрыш игрока B). Теорема1: В матричной игре нижн. чист. цена a не превосходит верх.цены b. Если a=b, то игра имеет седловую точку и чистую цену игры v=a=b. ( 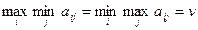). Т.е. если игра имеет седловую точку, то оптим. для игроков будет максиминная и минимаксная стратегии.

Однако если седловой точки нет, то решение затрудняется. Разность между максимином и минимаксом является нейтральным, и каждый игрок может улучшить свой результат за счёт данной области. Для получения выгоды игроки должны применять свои стратегии случайным образом.

Пусть p₁,…,p_m вероятности использования игроком А своих чистых стратегий (p_i>0, ∑p_i=1). Упорядоченное множество p=( p₁,…,p_m) называется смешанной стратегией игрока А. Аналогично и для игрока B (q=(q₁,…,q_n), q_j>0, ∑p_j=1). Таким образом, смешанной стратегией является полный набор вероятностей применения его чистых стратегий.

Ai	Bj	pi
B1	…	Bn
A1	a11	…	a1n	p1
		…		…
Am	am1	…	amn	pm
qj	q1	…	qn

Игрок А использует стратегию А₁ с вероятностью p₁, Игрок B – стратегию B₁ с вероятностью q₁. Т.к. игроки выбирают стратегии случайно, то вероятность выбора комбинаций (A_i,B_j) будет равна произведению вероятностей p_i*q_j. Тогда платёжная функция игры равна .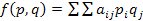

Таким образом, 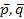- смешанные стратегии. Оптимальные смешанные стратегии определяются из

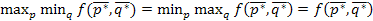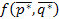, где - цена игры.

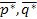- называются оптимальными смешанными стратегиями, если они образуют седловую точку для платежной матрицы 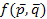, т.е. удовлетворяют условию

.

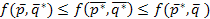Основная теорема МИ:В смешанных стратегиях любая конечная игра имеет седловую точку, или всякая матричная игра двух лиц с нулевой суммой имеет решение в смешанных стратегиях.

Критерий решения матричной игры:для того чтобы стратегии 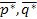были оптимальны для игроков А и В в игре с матрицей [a_ij]_m*n и ценой v, необходимо и достаточно выполнение неравенств:

.

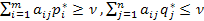Теорема: Если 1 из игроков придерживается своей оптимальной смешанной стратегии, то его выигрыш остается неизменным и равным цене игры независимо от того, какую стратегию применяет другой игрок, если тот не выходит за пределы своих активных стратегий (т.е. чья вероятность не равна 0).

Преобразование матрицы: убрать заведомо проигрышные стратегии, сделать все элем>0) не меняет v.

Решение смешанной игры ЛП:Рассмотрим случай, когда нижняя цена ≠ верхней цене игры и a_ij≥0. Оптимальную стратегию игрока B (не проиграет более v) берём из основной теоремы МИ ( 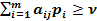). Делим всё на v и вводим замену q_j/v=y_j

Получаем систему: 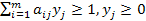, причём ∑y_j=1/v=µ. Т.к. игрок B стремится сделать свой гарантийный проигрыш v меньше, то следует максимизировать величину µ. В итоге получаем задачу ЛП: µ=∑y_j (max); 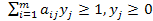, которая решается симплекс-методом. Зная y_j находим q_j и v. Аналогично для игрока А.

При небольших размерностях можно решать и графическим методом.

1) Критерий Байеса. (максимизируем средний выигрыш игрока А, т.е. перемножаем на известные вероятности и берём макс)

2) По Лапласу (максимизация среднего выигрыша, при неизвестных вероятностях – предполагаем равновероятность и берем макс)

3) По Вальду – критерий максимина max_imin_ja_ij

4) По Сэвиджу – выбираем стратегию, которая минимизирует максимальный риск min_jmax_ir_ij

5) По Гурвицу (пессимизм-оптимизм). За оптимальную стратегию принимается та стратегия, для которой достигается выигрыш

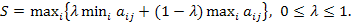
Пусть р_i - вероятность применения 1-м игроком стратегии i; q_j - вероятность применения 2-м игроком стратегии j;

Тогда пара двойственных задач будет иметь вид: для 1-го игрока:

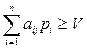
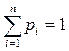(1)

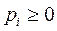
V → max - критерий оптимальности задачи для 1-го игрока

для 2-го игрока:

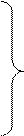
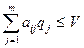
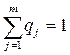(2)

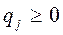
V → min - критерий оптимальности задачи для 2-го игрока

Игра – действительный или формальный конфликт, в котором имеется по крайней мере два участник, каждый из которых стремится к достижению собственных целей. Игра называется парной, если в ней участвуют только два игрока. Парная игра называется игрой с нулевой суммой, если сумма платежей равна нулю (проигрыш одного игрока равен выигрышу второго).

Однозначное описание выбора игрока в каждой из возможных ситуаций, при которой он должен сделать личный ход, называется стратегией игрока. Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии (строка\столбец), называется смешанной стратегией данного игрока.