Амплитудная модуляция гармонической несущей
Амплитудная модуляция – процесс изменения амплитуды несущего колебания, соответствующего изменению непрерывного информационного сигнала [3, 4].
При амплитудной модуляции мгновенная амплитуда несущего колебания:
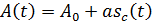 ; ; | (2) |
где 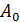 – амплитуда несущей;
– амплитуда несущей; 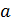 – коэффициент пропорциональности, выбираемый так, чтобы амплитуда
– коэффициент пропорциональности, выбираемый так, чтобы амплитуда 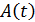 всегда была положительной. Частота и фаза несущего гармонического колебания при AM остаются неизменными.
всегда была положительной. Частота и фаза несущего гармонического колебания при AM остаются неизменными.
Для математического описания AM сигнала в (2) вместо коэффициента 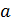 , зависящего от конкретной схемы модулятора, вводится индекс модуляции:
, зависящего от конкретной схемы модулятора, вводится индекс модуляции:
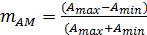 | (3) |
т.е. отношение разности между максимальным и минимальным значениями амплитуд AM сигнала к сумме этих значений. Для симметричного модулирующего сигнала 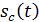 AM сигнал также симметричный, т.е.
AM сигнал также симметричный, т.е. 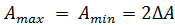 . Тогда индекс модуляции равен отношению максимального приращения амплитуды, к амплитуде несущей.
. Тогда индекс модуляции равен отношению максимального приращения амплитуды, к амплитуде несущей.
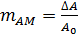 | (4) |
Физически индекс модуляции характеризует собой глубину амплитудной модуляции и может изменяться в пределах 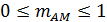 .
.
Таким образом, для любого AM сигнала справедливо:
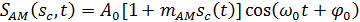 | (5) |
Амплитудная модуляция гармоническим колебанием. В простейшем случае модулирующий сигнал является гармоническим колебанием с частотой 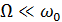 . При этом выражение
. При этом выражение
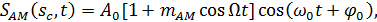 | (6) |
соответствует однотональному AM сигналу, представленному на рисунке 3 .
Однотональный AM сигнал можно представить в виде суммы трех гармонических составляющих с частотами: 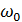 — несущей;
— несущей; 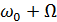 — верхней боковой и
— верхней боковой и 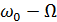 — нижней боковой:
— нижней боковой:
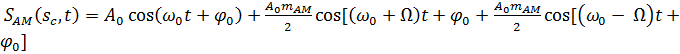 | (7) |
Спектральная диаграмма однотонального AM сигнала, построенная по (7), симметрична относительно несущей частоты 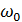 (рисунок 3, в). Амплитуды боковых колебаний с частотами
(рисунок 3, в). Амплитуды боковых колебаний с частотами 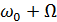 и
и 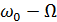 одинаковы и даже при
одинаковы и даже при 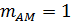 не превышают половины амплитуды несущего колебания
не превышают половины амплитуды несущего колебания 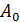 .
.
Гармонические модулирующие сигналы и соответственно однотональный AM сигнал на практике встречаются редко. В большинстве случаев модулирующие первичные сигналы 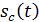 являются сложными функциями времени (рисунок 4, а). Любой сложный сигнал
являются сложными функциями времени (рисунок 4, а). Любой сложный сигнал 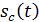 можно представить в виде конечной или бесконечной суммы гармонических составляющих, воспользовавшись рядом или интегралом Фурье. Каждая гармоническая составляющая сигнала
можно представить в виде конечной или бесконечной суммы гармонических составляющих, воспользовавшись рядом или интегралом Фурье. Каждая гармоническая составляющая сигнала 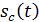 с частотой
с частотой 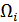 приведет к появлению в AM сигнале двух боковых составляющих с частотами
приведет к появлению в AM сигнале двух боковых составляющих с частотами 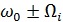 .
.
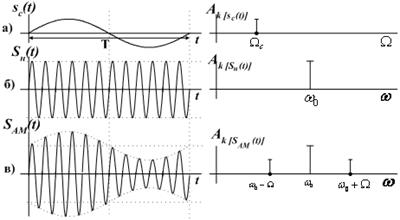
Рисунок 3 — Временные и спектральные диаграммы процесса формирования АМ гармонического колебания
Множеству гармонических составляющих в модулирующем сигнале с частотами 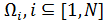 будет соответствовать множество боковых составляющих с частотами
будет соответствовать множество боковых составляющих с частотами 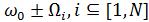 . Для наглядности такое преобразование спектра при AM показано на рисунке 4,б. Спектр сложномодулированного AM сигнала, помимо несущего колебания с частотой
. Для наглядности такое преобразование спектра при AM показано на рисунке 4,б. Спектр сложномодулированного AM сигнала, помимо несущего колебания с частотой 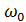 , содержит группы верхних и нижних боковых колебаний, образующих соответственно верхнюю боковую полосу и нижнюю боковую полосу AM сигнала.
, содержит группы верхних и нижних боковых колебаний, образующих соответственно верхнюю боковую полосу и нижнюю боковую полосу AM сигнала.
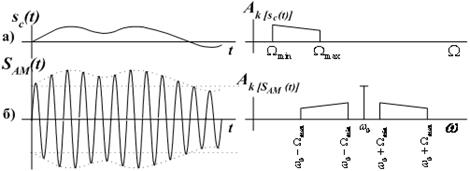
Рисунок 4 — Временные и спектральные диаграммы АМ сигнала
При этом верхняя боковая полоса частот является масштабной копией спектра информационного сигнала, сдвинутого в область высоких частот на величину 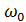 . Нижняя боковая полоса частот также повторяет спектральную диаграмму сигнала
. Нижняя боковая полоса частот также повторяет спектральную диаграмму сигнала 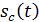 но частоты в ней располагаются в зеркальном порядке относительно несущей частоты
но частоты в ней располагаются в зеркальном порядке относительно несущей частоты 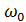 .
.
Ширина спектра AM сигнала 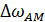 равна удвоенному значению наиболее высокой частоты
равна удвоенному значению наиболее высокой частоты 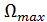 спектра модулирующего низкочастотного сигнала, т. е.
спектра модулирующего низкочастотного сигнала, т. е. 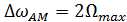 .
.
Наличие двух боковых полос обусловливает расширение занимаемой полосы частот примерно в два раза, по сравнению со спектром информационного сигнала. Мощность, приходящаяся на колебание несущей частоты, постоянна. Мощность, заключенная в боковых полосах, зависит от индекса модуляции и увеличивается с увеличением глубины модуляции. Однако даже в крайнем случае, когда 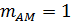 , только
, только 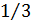 всей мощности колебания приходится на две боковые полосы [6].
всей мощности колебания приходится на две боковые полосы [6].
ПРАКТИЧЕСКАЯ ЧАСТЬ
