Исчисление предикатов

Формальные теории логических исчислений имеют исходные предпосылки сформулированные в виде аксиом, в качестве которых служат высказывания имеющие истинные значения в данной предметной области. Из множества с помощью цепочки логических вычислений выводятся теоремы. Для описания теорий используется язык, основными элементами которого является {AF}- алфавит и множество логических формул, образованных с использованием данного алфавита. A={X,N,P,L,Q,U,F}

Алфавит исчисления предикатов – упорядоченная система из множества переменных х, которые подразделяются на свободные и связанные , при помощи кванторов и принимающие значения на некотором множестве интерпретаций М. Множество констант N – подмножество М, множество функций, которые представляют собой f^m(t1,…,tm)- m- местный предикат функции от заданного количества термов. Термами могут выступать переменные, константы или функции, множество имен предикатов с помощью которых обозначаются отношения между объектами предметной области fⁿ(t1,…,tn)- n- местное отношение среди множества терм, L- множество унарных, либо бинарных логических связок и кванторов общности, существования, и вспомогательные знаки, которые используются для описания формул ( “(” ”)” ”[” ”]” ”,” )

L( )

Под предикатной формулой понимают ,атомарные, являющиеся переменными высказывания и сложные формулы, структурированные на основании атомарных и составных знаков алгоритма, Для определения значений формул, необходимо первоначально определить значение входящих в них термов. В состав термов получены значения констант из области М, либо функции вычисленные в этой области. Под интерпретацией понимается отображение на множество М предметной области , которая каждому предикату ставит в соответствие N местное отношение, каждой функции n местную операцию, предметной константе определенный элемент этого множества.

Рассмотрим предметную область на примере родственные отношения.

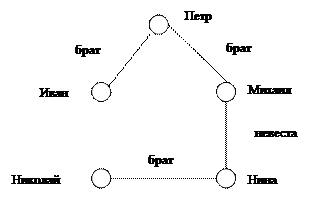
В 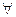конкретном случае- отношение

Брат(х,у)

Брат(Ник, f(Михаил))

Функциональная зависимость отражает отношение. Формулы представляют собой высказывания элементов. Она может быть истина или ложна . Логическое знание формулы определяется путем отображения на М всех термов входящих в предикаты и функции, при этом формула превращается в высказывание о том, что в данной предметной области между элементами выполняется данное отношение Формула называется выполнимой, если существует такая подстановка, при которой она может принимать истинное значение. Формула истина в данной интерпретации, если она выполнима в любой подстановке. Аксиом в теории определяются путем структурирования предметной области знаний 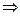, формируется множество высказываний и формул, отражающих суждения в данной предметной области- это множество образует систему аксиом теории, которая может быть выражена атомарными сложными высказываниями и формулами.

Структурирование предметной области:

1. Начинают с введения обозначений элементов интерпретаций

2. Значения элементов констант, далее поддерживаем обозначение для каждой функции

3. Подбирают названия для 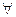существующего значения в области интерпретаций названия- обозначение предиката представляется атомарной формулой, построенной на основе выбранных обозначений констант и функций.

Можно составить множество атомарных формул имеющих истинное значение m- факта

Брат(Иван, Петр)

Брат((Петр, Михаил)

Если зададим цель Брат(Иван, Михаил), то такое отношение будет ложное, т. к. в области интерпретаций оно не было явно задано, следовательно описание необходимо дополнить сложной предметной формулой, для вывода истинности описания.

Брат(х, у)Брат

Брат(Ник,f(Михаил))

Функциональная зависимость отражает отношение. Формулы представляют собой высказывание элементов. Отношение между ними и функций заданные на ??? она может быть истина либо ложна. Логическое знание формулы определяется путем отображения на М всех термов ????????????

Для формализации дедуктивного вывода, наиболее удобным оказался альтернативный метод: поиск множества аксиом, при которых просматриваемая логическая формула false. Если такая интерпретация существует то расширенная формула не будет являться следствием из теории 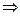прием заключается в описании выводимой формулы с помощью ее отрицания. Сущность этого метода основывается на формальной непротиворечивости теории из которых выводится доказательство. Если при добавлении к теории отражением формулы требующей доказательство можно вывести противоречие вида 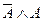, то такое предложение называют пустым . Наличие пустого множества доказывает ложность исходной посылки 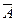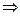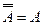. На этой основе была создана методика которая называется методом резолюций логического вывода, автор Робинсон- предложил правило резолюции на основании применения которого из клаузального множества может быть выведено пустое предложение. Возможность вывода пустого предложения доказать истинность выводимого заключения. (А1,…АN- аксиом ) 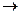P Доказательство выводимости эквивалентно доказательству ложности (А1,…АN ) 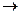P

Представим в виде клаузального множества S, которое представляет собой конъюнкцию предложений С1,С2,….,Сi,…,Ck

Каждое предложение клаузального множества представляет собой дизъюнкцию некоторого количества предикатных формул, либо литералов(позитивные \ негативные) Условием истинности клаузального множества является истинность всех входящих в него предложений, а условие ложности, ложность хотя бы одного из них. Условие ложность 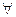выражения является пустое множество, т. е. наличие среди предложений клаузального множества{ 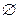} будет означать ложность всего множества , т. е. достаточно одного из литералов Pi оказаться истинным, как из этого следует отсутствие ложности этого выражения следовательно ложность S может быть доказана только путем нахождения пустого предложения.

Однако пустое предложение может не содержаться в явном виде в клаузальном множестве, однако его можно обнаружить в процессе дедукции на основании метода резолюции.

Правило резолюции формулируются так: из клаузального множества выбирается пара предложений, такая, что {Ci, Cg} одно из них содержит позитивный литерал, для которого существует негативный литерал во втором предложении, эти литералы должны иметь одно и тоже обозначение предикатов при одинаковом количестве его аргументов, при этом аргументы обоих литералов должны быть согласованы или унифицированы. Данные два предложения клаузального множества объединяются в одно называемое резолюцией из которого исключается пара литералов на основании которых происходит выбор двух исходных выражений резолюции становится новым предложением клаузального множества и в последствии может быть использована как и другие исходные предложения.

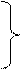
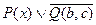
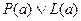(новое предложение)

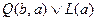
Получена резолюция на основании новых правил. Это характерно для формул логики предикатов, т. к. высказывание заведомо унифицировано, они не содержат аргументов, для унификации предикатных формул существуют правила:

Подстановка терма в переменную {t/x} подстановка записывается в виде упорядоченных пар, число которых может быть любым {t1/x,t2/x, . . . ,ti/xi . . .} в качестве терма может быть константа, функция либо другая переменная от переменной аргумента, при этом для 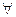группы подстановок унифицированные переменные не должны быть одинаковые т. е. при подстановке одной переменной нельзя присваивать два различных значения.

R, 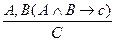Составим клаузальное множество:

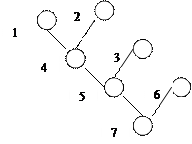
1)

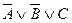
2) А

3) В

4)

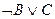
5) С

6)

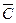
7) 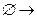истинность поставленной цели

Предметная область описывается следующими предпосылками.

Пример:

Агенты службы безопасности разыскивают всех въехавших в страну за исключением дипломатов.

В страну въехал шпион, однако распознать личность .………………

Шпион не является дипломатом, следует оценить правильность гипотезы. Среди агентов имеется шпион. Введем предикаты

Въехал(х) В(х)

Дипломат(х) Д(х)

Поиск(у,х) П(у,х)

Агент(у) А(у)

Выразим через эти предикаты, приведенные предпосылки и гипотезу.

1)

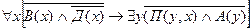
1.y=f(x)

2.

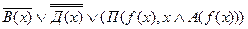
3.

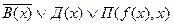
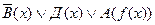
2)

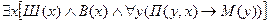
1.

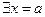
2.

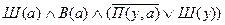
3.Ш(a)

B(a)

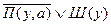
3)

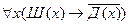
1.

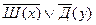
4)

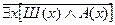
Метод доказательства от обратного 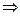гипотеза с отрицанием.

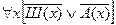
Получили следующее клаузальное множество.

1.

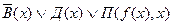
2.

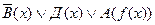
3. Ш(a)

4. B(a)

5.

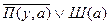
6.

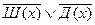
7. нами выдвинутая гипотеза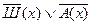

Для того, чтобы доказать гипотезу, нужно получить { 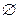}пустое множество предикатов. Варианты проведения доказательства.

Используем (3) и (6)

Доказательство:

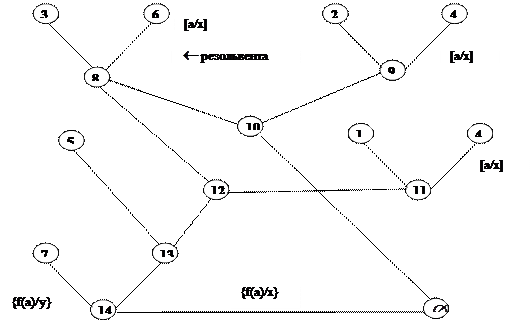8. 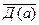- позитив

9. 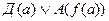- негатив

8+9 т. к. равно 10

10.A(f(a))

11.

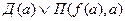
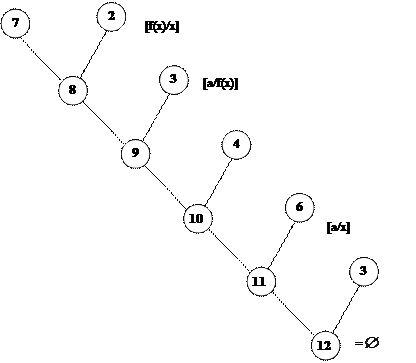12. 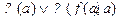?????????? Смотр 11

13.Ш(f(a))

14.

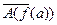
15. 14+10=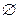

Доказательство от заключения.

8.

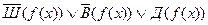
9.

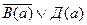
10.Д(a)

11.

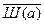
12.{ }

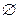Доказательство более эффективное.

Даны две посылки.

Некоторые студенты любят всех преподавателей. Ни один из студентов не любит невежд.

Заключение: следовательно ни один из преподов не является невеждой.

С(х)- студент

Р(у)- преподователь

L(х,у)- х любят у

Н(у)- невежда

Посылки:

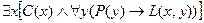
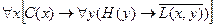
Заключение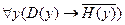

Клаузальные предложения:

1.С(а)

2.

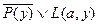
3.

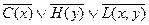
4.Р(в)

5.Н(в)

6.

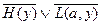
7.L(a,в)

8.

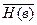
9.

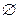
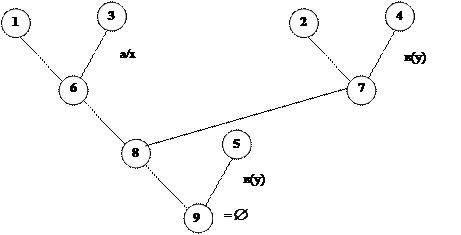Семантическое доказательство.

Семантическая резолюция является одной из эффективных модификаций принципа резолюции , в ней используется интерпретация для разделения множества дизъюнктов на два класса S1,S2, S1 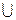S2=S

S1- пустое множество дизъюнктов, которое выполняется (принимает значение истина) , в этой интерпретации.

S2- не множество дизъюнктов, которые выполняются(лож) в этой интерпретации. Разрешается резальвирование дизъюнктов принадлежащих только разным множествам и запрещается образование резольвент от дизъюнктов входящих в одно и тоже множество, тем самым сокращается образование не нужных дизъюнктов т. к. только резальвированием из разных множеств можно получить пустой дизъюнкт.

Другим способом ограничения количества порождаемых дизъюнктов является упорядочение предиката. Если имеется упорядочение предикатных букв вида: Р1>P2> . . .>P_k, то разрешается резальвирование литеры обладающей большим порядком. Определим формально семантическую резолюцию.

Пусть I- интерпритации

P- упорядочение предикатных букв

Конечное множество дизъюнктов {Е1,Е2, . . . N}r 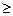1 называется семантический клаш??? относительно P и I. PI- клаш тогда и только тогда, когда Е1,Е2, . . .Е_r (электроны) N(ядро)- удолетворяют следующим условиям:

1) Е1,Е2, . . .Е_r – ложны в интерпритации I

2) При R1=N- где R1- резольвента, для каждого i=1,2,3, . . .,r, существует резольвента R_i+1 образованная из R_i и Е_i.

3) Резольвируемая литера в Е_i является наибольшей предикатной букве в Е_i i=1,2,3, . . .,r

4) Резольвента R_i+1, ложна в интерпритации I, такая резольвента называется PI резольвента, когда кончается перебор посылок, тогда заканчивается доказательство.Вывод из множества дизъюнктов S называют PI выводом, когда каждый дизъюнкт в выводе является или дизъюнктом S или PI резольвентом. Зададим интерпретацию и упорядоченность предикатных букв следующим образом: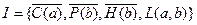

P>C>H>L

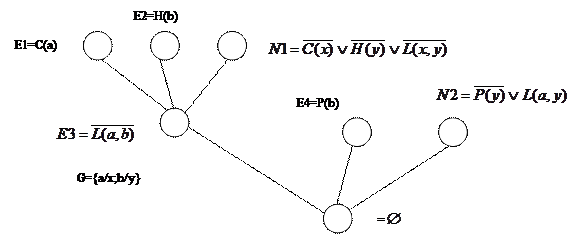E1,E2,N1- удовлетворяет всем четырем условиям и является клашным.

E3,E4,N_i=клашные(приводят к резольвенте)

(выше стоящие четыре условия) В семантической резолюции можно использовать любую упорядоченность ?????

Лекция №10

Сетевые модели.

В основу модели положена конструкция, называемая семантической сетью. Формально можно описать: H={I,C1, . . .,C_n ,G}

I- множество информационных единиц, которые отображают объекты, понятия, явления предметной области.

C_i- множество типов связи между информационными единицами

G- совокупность связей информационной единицы из набранного набора типов связи

В зависимости от типа использованной связи различают сети:

1.Классифицирующего типа.

2.Функционального типа.

3.Типа сценарий.

1. В классифицирующих сетях используются отношения структуризации типов абстрактное – конкретное , целое – частичное и др. Такие сети позволяют вводить в базы знаний иерархические отношения между информационными единицами.

2. Функциональные сети включают в себя отношения действия. На основе таких сетей можно строить вычислительные модели знаний, т. к. они позволяют описывать процедуры вычислений значение одних информационных единиц, через другие.

3. Сценарий использует отношения: средство- результат, орудие- действие. При помощи таких моделей, может быть восстановлены операции явно не описанные в БД.

Если в сетевой модели допускаются связи различного типа и множество этих типов не ограниченно, то такие модели принять называть семантической сетью. Первоначально семантическая сеть была задумана для модифицирования долговременной памяти, а в последствии стала одним из основных способов представления знаний в ИИ.

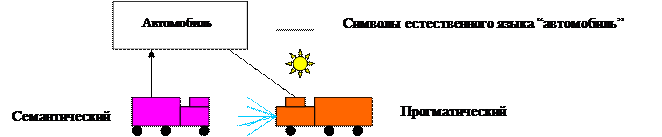Семантика- значение, смысл, слово действие, обстоятельство. Этот смысл передается с помощью некоторых средств. Обычно принимаются к сведению образы ассоциирующиеся с некоторым объектом предметной области и в зависимости от ситуации воспринимаемая как отдельная сущность. Семантика означает определенные отношения между выразительными ???средствами и объектами с которыми ассоциируются образы создаваемые этими средствами. Прагматика выразительные отношения?? между образами и пользователями можно выделить два функциональных уровня , которые связаны семантическими и прагматическими отношениями.

Слово воспринимается и создается образ, который может отличаться от исходного описывающего объекта. Первоначально в психологии изучались объекты, именуемые семантически с точки зрения ассоциативных свойств накапливаемых в долговременной памяти человека в процессе обучения. С развитием психологии стали изучаться семантические структуры, изучающие несколько взаимно- связанных объекта с общими ассоциативными свойствами. Далее изучались принципы действия человеческой памяти, которые позволяли представить долговременную память в виде иерархической структуры, где объекты представлялись различным уровнем абстракции, чем меньше , тем более конкретный объект. В качестве структуры была предложена модель

Куиллиан

Использована структура семантических отношений между словами человеческой речи или (концепт). Такая модель имитирует естественное понимание использование языка при общении между людьми.

Основная идея: описание класса которому принадлежит концепт, его прототип, т. е. пример использования и устранение связи со словами отображающие свойства концепта, т.е. того объекта который описывается данным словом.

Каждый концепт описывается:

1)классом

2)свойствами

3)прототипом

В модели Куиллиана, объекты представленны ассоциативными сетями, состоящей из вершины определенной концепты и дуг, показывающих отношения между концептами. Отношение класс ассоциируется с концептом транспорт, а св- во – легковой.Такая ассоциативная структура называется – плоской., концепция называется вершинами типа, а связанные ассоциативные слова – вершинами лексем??? Существует одна вершина типа и множество вершин лексем необходимых для ассоциативного определения концепта может существовать еще одна плоскость, в которой вершиной типа может являться транспорт. В качестве связи класс может иметь лексему машина. Свойства- преобразование энергии. Связи между отдельными плоскостями устанавливаются при помощи указателей которые связывают лексему в одной плоскости с вершиной типа в другой плоскости в долговременной памяти вранятся ассоциативные структуры трех типов:

1.Элементы вершин и лексем.

2.Свойства.

3.Указатели.

Элементы представлены фактами в виде объектов обобщенных понятий, событий описывающихся существительными или повествовательными предложениями.

Свойства- соответствует прилагательное, наречие, глагол. Указатели обеспечивают ассоциативные связи и не имеют явного выражения в виде слов языка.

указатель

[элемент]

(свойства)

Схема модели семантической сети может быть представлена

[элемент]

* * * *

( * * * * * * * )

атрибут значение

(1)связывает данный концепт, с концептом верхнего уровня

(2)свойства описания парами(атрибут \ значение)

Клиент- человек нанимающий специалиста.

[ клиент ]

* *

[ человек ] ( * * . . . )

* * *

нанимать специальность

1. Основное понятие является отношение is-a, которое характеризует свойства принадлежность элемента к определенному классу и характеризует отношение 1)абстрактное конкретное

человек is-a млекопитающие

2. ???- часть Part of Описывает возможность декомпозиции элемента на составные части.

Нос Part of лицо.

Используя такие отношения можно построить структурную схему, показывающую отношение принадлежности объекта соответствующим классам, и декомпозицию объекта для выделения объектов.

Иванов is-a

Мужчина is-a человек . . .

С помощью сети описаны факты Иванов мужчина

Мужчина Иванов

Отношение абстрактное конкретное is-a позволяет делать логические выводы. Использование иерархии наследования свойств благодаря которым Иванов может характеризоваться всеми свойствами которые соответствуют описанию человека. Кроме этого используя отношения Part of можно описать, что любой разумный человек имеет тело.

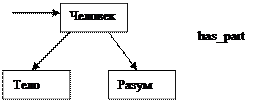
Выводы такого типа называются наследованием структуры, а ветвь is-a – наследование свойств. При расширении семантической сети, в нее возможно включать другие отношения, помимо отношений структур.

Отношение владеет

Отношение можно уточнить, указать t в течении которого был этот объект.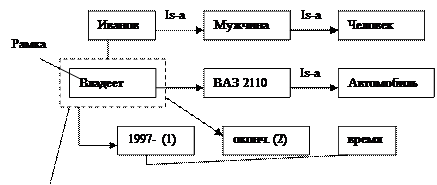

Абстрактное, нет объекта в предметной области ; концептуально т. к. имеет смысл только с Ивановым и его машиной. (1)начало , (2)окончание.

Семантическая модель обеспечивает описание области применения знаний используя различные отношения, которые выражаются смыслом словесного языка и могут содержать абстрактные вершины для раскрытия этого смысла. Большинство моделей семантических сетей, имеет унифицированную структуру отражающую декомпозицию объекта либо применимую к факторам действия.

Преимущества: возможность наследования ожидаемых значений и использование значений по умолчанию ??? не гарантирует такой же достоверности, какой обладают логические модули. Это обусловлено использованием наследования свойств и структур.

Не значит, что Иванов является военно обязанным. Принцип наследования не позволяет исключить из свойств Иванова состояние учета в воинкомате. Для обеспечения правильного вывода заключений, требуется тестирование и введение дополнительных свойств, исключающих неправильное истолкование.

Лекция №11