Пример расчета экстремума функции методом средней точки

Постановка задачи. Найти минимум функции f(x) = (1-x)² +3(x-5)²+8 с точностью l=0,01.

Выбираем начальный интервал [-10, 10]. Результаты расчетов представлены в таблице 2.10.

Таблица 2.10

Расчет экстремума функции f(x) = (1-x)² +3(x-5)²+8 методом средней точки.

№	ak	bk		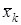f(x)	f'(x)	|bk-ak|	Критерий
	-10.000	10.000	0.000	84.000	-32.000	20.000	Не достигнут
	0.000	10.000	5.000	24.000	8.000	10.000	Не достигнут
	0.000	5.000	2.500	29.000	-12.000	5.000	Не достигнут
	2.500	5.000	3.750	20.250	-2.000	2.500	Не достигнут
	3.750	5.000	4.375	20.563	3.000	1.250	Не достигнут
	3.750	4.375	4.063	20.016	0.500	0.625	Не достигнут
	3.750	4.063	3.906	20.035	-0.750	0.313	Не достигнут
	3.906	4.063	3.984	20.001	-0.125	0.156	Не достигнут
	3.984	4.063	4.023	20.002	0.188	0.078	Не достигнут
	3.984	4.023	4.004	20.000	0.031	0.039	Не достигнут
	3.984	4.004	3.994	20.000	-0.047	0.020	Не достигнут
	3.994	4.004	3.999	20.000	-0.008	0.010	Достигнут

Таким образом, на двенадцатой итерации с точности 0,01 найден экстремум функции f(x) = (1-x)² +3(x-5)²+8, который находится в точке 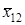=3,999.

2.3.3. Метод кубической аппроксимации.

В методе кубической аппроксимации при построении многочлена, аппроксимирующего минимизируемую функцию, помимо значений функции используются и значения ее производных.

Предполагается, что заданы две точки x₁ и x₂ таким образом, что минимум функции f(x) находится внутри интервала [x₁; x₂], известны значения функции в этих точках f(x₁)=f₁, f(x₂)=f₂ и значения производных f'(x₁)=f'₁, f'(x₂)=f'₂. Аппроксимирующая функция задана полиномом, который имеет вид:

Н(x) = f₁+ a₁(x - x₁) + a₂(x - x₁)(x - x₂) + a₃(x - x₁)²(x - x₂)

с коэффициентами

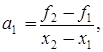
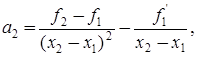
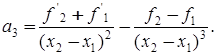
Несложно проверить, что H(x₁)=f₁, H(x₂)=f₂, H΄(x₁)=f΄₁, H΄(x₂)=f΄₂. Производная H΄(x) является квадратичной функцией, непрерывной на отрезке [x₁; x₂] и имеющей на его концах различные знаки. Поэтому, в интервале она может изменить знак лишь один раз в точке 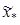, которая является стационарной точкой многочлена H(x), а именно точкой его минимума, так как производная меняет знак с минуса на плюс. Из необходимого условия H΄(x)=0 экстремума этого многочлена получаем квадратичное уравнение

.

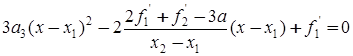Его решение определяется следующим образом:

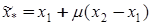, где

, .

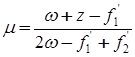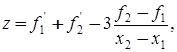
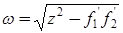Если 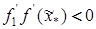, то новый интервал будет равен 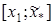, иначе 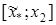. Вычисления прекращаются, когда длина конечного интервала не станет меньше заданной точности.

Алгоритм метода кубической аппроксимации.

Начальный этап. Задать начальный интервал [x₁, x₂] и точность поиска l. Перейти к основному этапу.

Основной этап. Шаг 1. Вычислить значения функции f(x₁)=f₁, f(x₂)=f₂ и значения производных f'(x₁)=f'₁, f'(x₂)=f'₂. Рассчитать коэффициенты 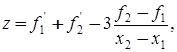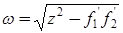, 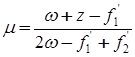и оптимальное решение
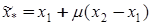. Перейти к шагу 2.

Шаг 2. Если |x₂ - x₁| < l, то закончить расчет, оптимальное решение находится в точке 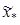, иначе перейти к шагу 3.

Шаг 3. Если 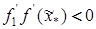, то x₁=x₁, x₂= 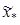, иначе x₁= 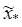, x₂= x₂, перейти к шагу 1.

Пример расчета экстремума функции методом кубической аппроксимации.

Постановка задачи.Найти минимум функции f(x) = x² –16/x методом кубической аппроксимации. Выбираем начальный интервал [-5; 10] и точность поиска равную 0,1. Результаты расчета приведены в таблице 2.11.

Таблица 2.11

Результаты расчета минимума функции f(x) = x² –16/x методом кубической аппроксимации.

№	x1	x2	f(x1)	f(x2)	f'(x1)	f'(x2)	z	ω	μ		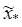f'( 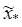)	|x2-x1|	Критерий
	-5.0	10.0	28.20	98.400	-9.360	20.160	-3.240	14.114	0.350	0.256	245.150	15.00	Не достигнут
	-5.0	0.26	28.20	-62.498	-9.360	245.150	287.561	291.523	0.703	-1.307	6.745	5.256	Не достигнут
	-5.0	-1.31	28.20	13.947	-9.360	6.745	8.965	11.979	0.756	-2.207	-1.129	3.693	Не достигнут
	-2.2	-1.31	12.12	13.947	-1.129	6.745	-0.476	2.800	0.256	-1.976	0.143	0.899	Не достигнут
	-2.2	-1.98	12.12	12.002	-1.129	0.143	0.560	0.689	0.897	-2.000	-0.001	0.231	Не достигнут
	-2.0	-1.98	12.00	12.002	-0.001	0.143	-0.070	0.071	0.005	-2.000	0.000	0.024	Достигнут

Таким образом, на шестом шаге с точностью 0,01 найден экстремум функции 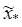=-2,000,который совпадает с экстремумом, полученным аналитически.

3. ВАРИАНТЫ ЗАДАНИЙ ДЛЯ ВЫПОЛНЕНИЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ.

Выполнение заданий предусматривает:

- для заданной функции поиск экстремума аналитически и его анализ;

- определение начального интервала неопределенности методом сканирования, построение графика функции;

- поиск минимума функции методами одномерной оптимизации, рассмотренными выше, при заданных параметрах;

- выводы об эффективности методов.

Требования к отчету:

В отчете должны быть представлены результаты выполнения указанных этапов и выводы к ним. Отчет представляется индивидуально каждым студентом.

Варианты заданий приведены в таблице 3.1

Таблица 3.1

Варианты заданий

№	Вид функции f(x)	Точность
	x2 – 2x + 1	0,010
	x2 + x + 5	0,010
	x2 + 3x – 7	0,020
	x2 + 5x	0,010
	x2 + x – 1	0,015
	2x2 + x	0,010
	3x2 – x	0,005
	5x2 – 2x	0,010
	3x2 + 2x –1	0,020
	2x2 – x +5	0,010
	6x2 + 8x	0,010
	27/x + 3x	0,020
	x2 + x + 10	0,020
	x2 – x +13	0,015
	x2 + x +8	0,015
	x2 + 9x	0,010
	x2 – 6x	0,010
	16/x + 4x	0,020
	9x2 + 5x –3	0,020
	3x2 + 8x + 2	0,015
	3x2 + 18x – 6	0,010
	x2 + 15x	0,015
	x2 + 3x + 3	0,010
	x2 – 2x – 2	0,010
	8/x + 2x	0,010
	7x2 + 4x + 1	0,015
	2x2 – 3x – 5	0,010
	3x2 + 8x - 12	0,015
	5x2 + 8x – 4	0,010
	7x2 + 10x + 1	0,010

СПИСОК ЛИТЕРАТУРЫ

1. Мочалов С.П. Методы оптимизации металлургических процессов: Учебное пособие / КузПИ. –Кемерово, 1989.- 81с.

2. А.В. Аттеков, С.В. Галкин, В.С. Зарубин. Методы оптимизации: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 440с. (Сер. Математика в техническом университете; Вып.XIV).

3. Поляк Б. Т. Введение в оптимизацию. -М.: Наука, 1983.

4. Моисеев Н. Н., Иванилов Ю. П., Столярова Е. М. Методы оптимизации. -М.: Наука, 1975.

5. Банди. Методы оптимизации. -М.: Радио и связь, 1988.

6. Курицкий Б.Я. Поиск оптимальных решений средствами Ecxel 7.0. –СПб.: BHV – Санкт-Петербург, 1997.- 384с., ил.