Использование математического ожидания и стандартного отклонения для оценки риска

В результате использования правила максимизации ожидаемых доходов мы получаем оценку для каждого исхода в виде таблицы доходов, чтобы выбрать "наилучшее" решение. В ней приводится разброс доходов для каждого исхода, анализ которого дает возможность оценитъ риск каждого решения. Альтернативный подход к оценке риска заключается в вычислении стандартного отклонения доходов, как это делается для любого вида распределений. Именно таким образом в нижеприведенном примере сравниваются два варианта инвестиций. Несмотря на то, что в этом случае и в примере с закупкой пирожных арифметически два варианта решаются совершенно одинаково, между ними существует значительная разница. Решение, принятое для покупки пирожных, остается неизменным изо дня в день, и идея ожидаемых средних доходов проста для понимания, тогда как решение об инвестициях принимается лишь однажды, что затрудняет понимание значения ожидаемых доходов на практике.

ПримерНиже приведены возможные чистые доходы и их вероятности двух вариантов вложений.

	Сравнение вариантов решений
Чистая прибыль, тыс. руб.	-3	-2	-1
Вероятности: Инвестиция 1			0, 1	0, 2	0,3	0, 2	0,2
Инвестиция 2	0,1	0, 1	0, 1	0, 1	0,1	0, 1	0,2	0,2

Ожидаемая прибыль:

ЕMV (ивестиция 1) = (- 3 х 0) + (- 2 х 0) + (- 1 х 0,1) + (0 х 0,2) + (1 х 0,3) +

+ (2 х 0,3) + (3 х 0,2) + (4 х 0)= 1200 руб.

ЕMV (инвестиция 2) = (- 3 х 0,1) + (- 2 х 0,1) + (- 1 х 0,1) + (0 х 0,1) +

+ (1 х 0,1) + (2 х 0,1) + (3 х 0,2) + (4 х 0,2) = 1100 руб.

Если принимать во внимание только ожидаемую прибыль, то инвестиция 1 безусловно лучше. Если бы решение об инвестициях принималось много раз при одних и тех же условиях, то тогда прибыль в среднем составляла бы 1200 ф. ст. Однако правило принятия решений не учитывает риск, связанный с инвестициями, т.е. "разброс" возможных исходов.

Этот риск может быть определен с помощью дисперсии и стандартного отклонения прибыли.

Дисперсия вероятностного распределения представляет собой:

Дисперсия = S рх² — (ЕMV (х)) ²;

ЕMV (х) = Sр х,

где х — прибыль на инвестиции; р — вероятность получения данной прибыли.

Расчет средней прибыли и дисперсии для инвестиций

Прибыль,тыс. руб.	Инвестиция 1	Инвестиция 2
X	Р	рх	р*х2	Р	рх	Р*х2
-3				0,1	-0,3	0,9
-2				0,1	- 0,2	0,4
-1	0,1	-0,1	0,1	0,1	- 0,1	0,1
	0,2			0,1
	0,3	0,3	0,3	0,1	0,1	0,1
	0,2	0,4	0,8	0,1	0,2	0,4
	0,2	0,6	1,8	0,2	0,6	1,8
				0,2	0,8	3,2
Всего	1,0	1,2	3,0	1,0	1,1	6,9

Дисперсия 1= 3,0 - 1,2² = 1,56 (тыс. руб. в квадрате)

Следовательно,Стандартное отклонение прибыли = Ö1,560 = 1,250 тыс.руб. =1250 руб.

Дисперсия 2= 6,9 - 1,1 ² = 5,69 ² (тыс. руб. в квадрате) . Следовательно,

Стандартное отклонение прибыли = Ö5,69 = 2385 руб.

Риск по варианту для инвестиции 1 меньше, так как дисперсия прибыли намного меньше, чем для инвестиции 2.

Математическое ожидание и стандартное отклонение для двух вариантов инвестиций, ф. ст.

Инвестиция	Ожидаемая прибыль	Стандартное отклонение

Анализируя данные таблицы, можно прийти к выводу, что как большая ожидаемая прибыль, так и меньший "разброс" говорят в пользу инвестиции 1.

Деревья решений

На практике результат одного решения заставляет нас принимать следующее и т.д. Для этой последовательности используют схему дерева решения.

Дерево решений — это графическое отражение процесса, которое определяет альтернативы решения, состояния природы и их соот­ветствующие вероятности отдачи для каждой комбинации альтер­натив и состояний природы.

Хотя мы можем использовать все критерии решений, которые были обсуждены выше, ожидаемая отдача в денежном выражении (ЕМУ) — это наиболее используемый и обычно наиболее соответ­ствующий критерий для анализа деревьев решений.

Анализ проблемы с использованием дерева целей включает в себя пять шагов:

1. Определить проблему.

2. Структурировать или нарисовать дерево целей.

3. Назначить вероятности к состояниям природы.

4. Оценить отдачу для каждой возможной комбинации альтер­натив и состояний природы.

5. Решить проблему, вычисляя ожидаемую отдачу в денежном выражении (ЕМУ) для каждого узла, состояния природы. Это делается путем движения назад, что значит: начиная справа от дерева и работая назад по узлам решений дерева.

Символы, используемые для дерева решений: a) —этоузел решения, из которого может быть выбрана одна или несколько альтернатив; б) O— это узел состояния природы.

ПРИМЕР

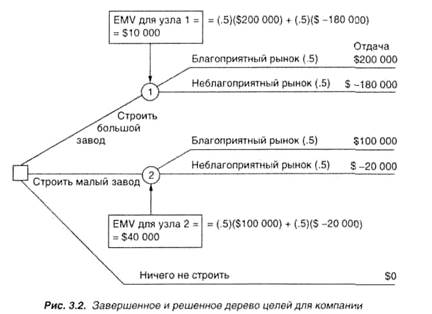
Законченное и решенное дерево целей для компании представлено на рис.. Заметим, что отдачи помешены в правой части каждой ветви дерева. Вероятности (впервые использованные компанией в примере 4) помешены в скобках рядом с каждым состоянием природы. Ожидаемая отдача в денежном выражении для каждого состояния природы затем вычисляется и помешается в соответствующих узлах. ЕМУ(1-гоузла) = $10000.

Это отражает ветвь от узла решения «строить большой завод».

ЕМУ(2-го узла) = $40 000.

Не строить завод или ничего не делать имеет, конечно, отдачу $ 0. Выбирается ветвь, начинающаяся в узле решения, ведущая к узлу состояния природы с наивысшим ЕМУ. В рассматриваемом случае компанией должен быть построен малый завод.