Растровая развертка отрезка

Так как в подавляющем большинстве графические устройства являются растровыми, то есть представляют изображение в виде прямоугольной матрицы (сетки, целочисленной решетки) пикселей (растра), то, естественно, возникает необходимость в растровых алгоритмах.

Хотя большинство графических библиотек содержат внутри себя достаточное количество простейших растровых алгоритмов, таких, как: переведение идеального объекта (отрезка, окружности и др.) в их растровые образы; обработка растровых изображений, тем не менее, часто возникает необходимость явного построения растровых алгоритмов.

3.1 Растровая развертка отрезка

Достаточно важным понятием для растровой сетки является связность - возможность соединения двух пикселей растровой линией, то есть последовательным набором пикселей. При этом возникает вопрос, когда пиксели(Х₁,у₁) и (X₂,y₂) можно считать соседними. Вводится два понятия связности:

- 4-связность, когда пиксели считаются соседними, если либо их х-координаты, либо у-координаты отличаются на единицу, то есть |х1-х2| + |y1-y2|≤1;

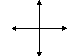Рис.68

- 8-связность, когда пиксели считаются соседними, если их х- и у-координаты отличаются не более чем на единицу, то есть |x1 – x2| ≤ 1, |у1 – У2| ≤ 1

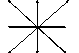Рис.69

Так как понятие линии базируется на понятии связности, то естественным образом возникает понятие 4- и 8-связных линий. Поэтому, когда мы говорим о растровом представлении, например, отрезка, то следует ясно понимать, о каком именно представлении идет речь. При этом нужно иметь в виду, что растровое представление объекта не является единственным и возможны различные способы построения.

В качестве линии на растровой сетке выступает набор пикселей P1, P2, …, Pn, где любые два пикселя Pi,Pi+1 являются соседними.

Рис.70

Рассмотрим задачу построения растрового изображения отрезка, соединяющего точки (x1,y1) и (x2,y2).

Для простоты будем считать, что 0 ≤ y2-y1 ≤ x2-x1

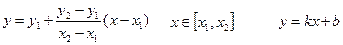Тогда отрезок описывается следующим уравнением

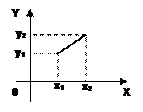Рис.71

Простейший алгоритм растрового представления отрезка имеет вид:

//File Linel.cpp

void Line(int xl, int yl, int x2, int y2, int color)

{

double k=(y2-yl)/(x2-xl);

double b=yl-k*xl;

for (int x=xl; x<=x2; x++)

putpixel (x, round (k*x+b), color);

}

Алгоритм Брезенхейма

В 1965 году Брезенхеймом был предложен простой целочисленный алгоритм для растрового построения отрезка, первоначально предназначенный для использования в графопостроителях

При построении растрового изображения отрезка всегда выбирается ближайший по вертикали пиксель. При этомиз двух точек А и В выбирается та, которая ближе к исходной прямой (в данном случае выбирается точка А, так как а<Ь). Для этого вводится число d, равное (x2 – x1)(b — а).

В случае d>0 значение у от предыдущей точки увеличивается на 1, a d -на 2(∆у — ∆х)

В противном случае значение у не изменяется, а значение d заменяется на 2∆у.

//File Line2.cpp

void Line{int xl, int yl, int x2, int y2, int color)

{

int dx=x2-xl;

int dy=y2-yl;

int d=(dy<<l)-dx;

int dl=dy << l;

int d2=(dy-dx) << l;

putpixel (xl, yl, color);

for (int x=x1+1, y=yl; x<=x2; x++)

{

if (d>0)

{

d+=d2;

y+=1;

}

else

d+=d1;

putpixel (x, y, color);

}

}