Алгоритм метода Пауэлла
Начальный этап. Выбрать x1 - начальную точку, Dx - величину шага по оси x. Задать точность поиска по х и f(x) e1=0,01 и e2=0,1. Перейти к основному этапу.
Основной этап. Шаг 1. Вычислить x2 = x1 + Dx.
Шаг 2. Вычислить f(x1), f(x2).
Шаг 3. Если f(x1) > f(x2), положить x3 = x1 + 2Dx. Если f(x1) £ f(x2), положить x3 = x1 - Dx.
Шаг 4. Вычислить f(x3) и найти Fмин = min{f1, f2, f3}.
Xмин = (×) xi, которая соответствует Fмин.
Шаг 5. По трем точкам x1, x2, x3 вычислить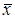 
используя формулу для оценивания с помощью квадратичной аппроксимации.
Шаг 6. Проверка на окончание поиска:
- является ли разность Xмин - 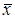достаточно малой(/Xмин - 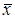/<e1)?
- является ли разность Fмин - f( 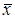) достаточно малой (/Fмин - f( 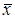)/<e2)?
Если оба условия выполняются, закончить поиск. В противном случае перейти к шагу 7.
Шаг 7. Выбрать “наилучшую” точку (Xмин или 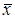) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 4.
Необходимо отметить, что за счет последовательных приближений, совмещенных с квадратичной аппроксимацией, метод имеет высокую эффективность.
Пример расчета экстремума функции методом Пауэлла.
Постановка задачи. Рассчитать минимум функции f(x) = (3-x)2 + 2x-1 методом Паулла. Выбираем начальную точку x1=0 и Dx=1 - величину шага по оси x, а также точность поиска по х и f(x) e1=0,01 и e2=0,1.
Результаты расчета минимума функции f(x) = (3-x)2 + 2x-1 представлены в таблице 2.8.
Таблица 2.8
Результаты расчета минимума функции f(x) = (3-x)2 + 2x-1 методом Пауэлла
| x1 | x2 | x3 | f(x1) | f(x2) | f(x3) | a0 | a1 | a2 | xmin | f(xmin) | xопт | f(xопт) | xmin-xопт | f(xmin)-f(xопт) |
| 0,00 | 4,00 | 8,00 | 8,00 | 8,00 | 40,00 | 8,00 | 0,00 | 3,00 | 0,00 | 8,00 | 2,00 | 4,00 | 2,00 | 4,00 |
| 0,00 | 2,00 | 4,00 | 8,00 | 4,00 | 8,00 | 8,00 | -2,00 | 1,00 | 2,00 | 4,00 | 2,00 | 4,00 | 0,00 | 0,00 |
Из расчетов видно, что экстремум найден за одну итерацию, что говорит о высокой эффективности метода.
МЕТОДЫ С ИСПОЛЬЗОВАНИЕМ ПРОИЗВОДНЫХ
Рассмотренные в предыдущем разделе методы поиска основываются на предположениях об унимодальности и в ряде случаев о непрерывности исследуемой целевой функции. Целесообразно предположить, что если в дополнении к условию непрерывности ввести требование дифференцируемости функции, то эффективность поисковых процедур можно существенно повысить.
2.3.1. Метод Ньютона.
В рамках схемы Ньютона предполагается, что функция f дважды дифференцируема. Работа алгоритма начинается в точках x1, которая представляет начальное приближение и строится по рекурентному соотношению xk+1 = xk - [f'(xk)/f''(xk)], где присутствуют первая и вторая производные. Однако, в зависимости от выбора начальной точки и вида функции алгоритм может как сходиться к истинной стационарной точке, так и расходиться. Несмотря на этот недостаток метод Ньютона требует наименьшего количества расчетов функции.