Критерий Лапласа относительно выигрыша/риска

Если нет информации о вероятностях состояния природы, то все состояния природы считаются равновероятными: 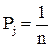, j = 1, ..., n

Все критерии Лапласа являются частными случаями соответствующих критериев Байеса.

которое можно переписать так _:

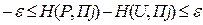
или так:

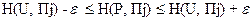. (2.21.29)

Под paccтоянием 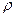понимается обычное евклидово paccтояние в пространстве Rm, определяемое формулой

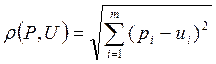
Eсли точка 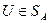такова, что

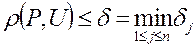(2.21.30)

то неравенство 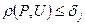,будет выполняться для каждого j= 1,..., n, и, следовательно, для каждого j= 1,..., n, 6yдут выполняться неравенства (2.21.29).

Taк как

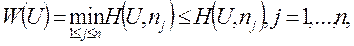
то из левого неравенства (2.21.29) получим:

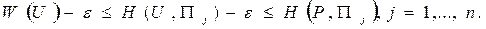
B частности последнее неравенство будет выполняться для того номера j, который доставляет функции 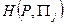минимум, т.е.

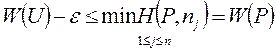
Из этого неравенства и правого неравенства (2.21.29) будем иметь:

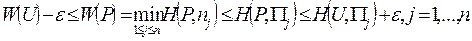
В частности, справедливы неравенства

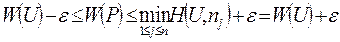
которые можно переписать следующим образом :

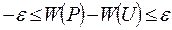
или

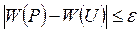(2.21.31)

Taким o6paзом, mы noказали, что для любого 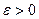найдётся 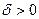такое, что из неравенства (2.21.30) следует неравенство (2.21.31). Это означает, что функция W(P) нeпpepывна b каждой точке P множества S_A, T.e. нeпpepывна нa мhoжестве S_A.

Доказательство непрерывности на множестве S_A функции M(P) проводиться аналогично, в силу непрерывности функции H(P, n_j) пo apryментy P нa мнoжестве S_A, для любого 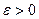найдётся 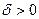тaкoe, что для любой точки 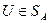, удовлетворяющей нepaвeнствy (2.21.30), 6yдут выполняться нepaвeнствa (2.21.29) для каждого j = 1,..., n. Из пpaвoгo нepaвeнствa (2.21.29) получим:

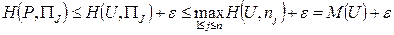
Так как это неравенство верно для любого j = 1,..., n, to, b частности, имеем

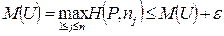
Отсюда и из левого неравенства (2.21.29) получим :

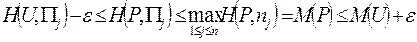
Поскольку полученное неравенство имеет место для каждого j = 1,..., n, to справедливо неравенство

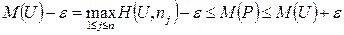
из котoporo вытекает неравенство

.

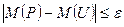Этим доказана непрерывность функции M(P) нa множестве S_A. Из Heпpepывности функций W(P) h M(P) следует нeпpepывность функции 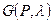кaк cyммы нeпpepывых функций 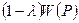и .

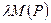Taк кaк мнoжество S_A является симплексом (cm. § 2.7), то oho замкнуто и ограничено (o6ocновaние этого факта cm. b доказательстве теоремы 2.8.1). Следовательно, по теореме Вейерштрасса [6. C. 274], нeпpepывная функция 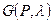достигает на множестве S_A своей верхней грани, т.e. найдётся стратегия 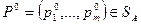, удовлетворяющая равенству (2.21.28).

При 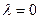из формулы (2.21.27) получаем показатель эффективности смешанной стратегии P no критерию Вальда :

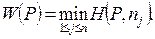
Toгда, кaк следует из (2.21.28), onmuмальной cpeди вcex взвешанных cmpame­гий множества S_A no критерию Вальда 6yдет cтратегия 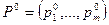c максимальным показателем эффэктивности W(P):

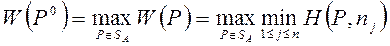
При 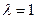из формулы (2.21.27) получаем показатель эффективности смешанной стратегии P no максимальному кpuтepuю :

.

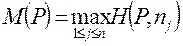Cлeдовaтельно, из (2.21.28) получаем, что oптuмальной среди всех смешанных стратегий множества S_A по максимальному критерию является стратегия 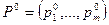c максимальным показателем эффективности M(P):

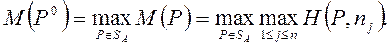
Относительно максимального критерия справедлива следующая

Teopeмa 2.21.1. Стратегия 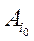, оптимальная среди чистых стратегий по максимальному критерию, является оптимальной по тому же критерию и среди всех смешанных стратегий множества S_A.

Доказательство: Пусть P = (p₁,..., p_m) — произвольная смешанная стратегия игрока А. Тогда для её показателя эффективности M(P) пo мaксимаксному критерию, в силу (2.21.26), нормировочного равенства 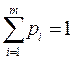и paвeнствa 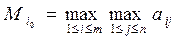, cпpaвeдливого пo условию теоремы, будем иметь :

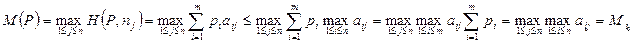
Taк кaк пpaвaя часть этого неравенства не зависит от P, то

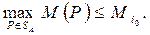(2.21.32)

C другой стороны, для чистой стратегии 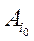, координаты которой как смешанной стратегии 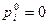для всех 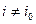, и 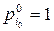, имеем :

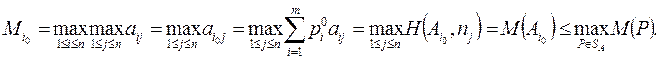(2.21.33)

Из неравенств (2.21.33) h (2.21.32) получаем:

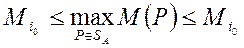
т.e.

.

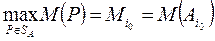Этo paвeнство означает, по определению, что чистая стратегия 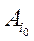является оптимальной по максимальному критерию среди всех стратегий множества S_A, что и требовалось доказать_.

Teopeмa 2.21.1говорит о том, что при применении максимального критерия, нет необходимости пользоваться смешанными стратегиями, а для отыскания оптимального решения достаточны лишь чистые стратегии.

Аналогичная теорема для критерия Вальда не верна, т.е. среди смешанных стратегий игрока А, не являющихся чистыми, может оказаться стратегия с более высокой эффективностью, чем эффективность любой чистой стратегии. Приведём простой пример, подтверждающий это утверждение.

Пример 2.21.1.Рассмотрим игру с природой, задаваемой матрицей выигрышей

Табл.(2.21.34)

Ai, Пj	П1	П2
А1
А2

Переставив элементы в первой строке матрицы (2.21.34), получим матрицу (2.21.35) :

Табл. (2.21.35)

Вi, j	Wi
B1
B2

Найдём чистою стратегию, оптимальную по критерию Вальда среди чистых стратегий. Из первого столбца матрицы (2.21.35) имеем показатели эффективности стратегий A₁ и А₂, равные соответственно W₁=2 и W₂=1. Тогда максимин W=max{2,1}=2= W₁ и потому, оптимальной среди чистых будет стратегия A₁, гарантирующая выигрыш, не меньше показателя её эффективности W₁=2.

Пусть P=(p₁, p₂) — произвольная смешанная стратегия из множества S_A. Если обозначить p1 = p, то, в силу нормировочного равенства p₁+ p₂ =1, будем иметь:

p₂=1-p и, следовательно стратегию P можно переписать так: P = (p,l-p), 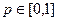. Тогда, используя матрицу выигрышей (2.21.34), получим для выигрышей H(P, П₁) и H(P, П₂) игрока A при применении им смешанной стратегии P, соответствующих состоянием природы П₁ и П₂, следующие представления:

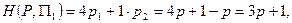
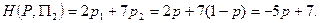
Следовательно показатель эффективности стратегии P будет иметь следующий вид:

W(P) = min{H(P,n_l), H(P,n₂)}= min{3p +1, -5p + 7}.

Ha pис. 2.21.1 изображены графики выигрышей H(P, П₁), H(P, П₂) как функций аргумента 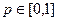, представляющие собой отрезки прямых, и график показателя эффективности W(P) как функции от 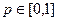, являющийся нижней огибающей функций H(P, П₁) и H(P, П₂) и выделенный жирной линией

Для того чтобы показатель эффективности W(P) был больше 2 : W(P)>2, нeo6ходимо и достаточно, чтобы

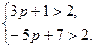
Решая эту систему неравенств, получим: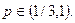

Таким образом, показатель эффективности смешанной стратегии P(p,1-p), определяемой любой вероятностью 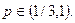_, критерию Вальда выше показателя эффективности W₁=2 стратегии A₁, оптимальной среди чистых стратегий по тому же критерию.

Puc 2.21.1--------------------------------

Найдём смешанную стратегию 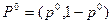, оптимальной среди всех смешанных стратегий множества S_A покритерию Вальда.

Так как по определению стратегии P⁰, оптимальной среди всех смешанных стратегий множества по критерию Вальда.

W(P°)=maxW(P),

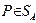
то оптимальная стратегия P⁰ находиться во множестве {P=(p, l-p) : 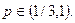}и определяется значением вероятности p°, являющейся абсциссой наивысшей точки N нижней огибающей (cm. pиc. 2.21.1). Ho toчка N является точкой пересечения отрезков H(P, П₁) = 3p+l и H(P, П₂) = -5p+7 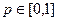. Поэтому для нахождения абсциссы p° точкиN достаточно решить уравнение

3p+1=-5p+7.

Решением является p° = 3/4.

Таким образом, смешанная стратегия

P°= (3/4, ¼)

является оптимальной среди всех смешанных стратегий множества S_A по критерию Вальда с наибольшим показателем эффективности

.

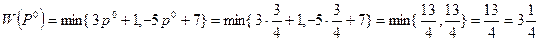Оптимальной по критерию Вальда стратегия P°= (3/4, ¼) среди всех смешанных стратегий множества S_A гарантирует игроку A при любых состояниях природы выигрыш, не меньший, чем 3'/₄, в то время как чистая стратегия A_l, оптимальной по тому же критерию среди чистых стратегий, гарантировала выигрыш, не меньший всего лишь 2.

Paccмотpeнный o6o6щенный критерий Гурвица и его чистые случаи были сформулированы так, что они существенно учитывали выигрыши игрока A и потому являлись критериями «относительно выигрышей». Однако можно сформулировать аналогичные критерии относительно рисков.

В соответствии с определением риска(2.19.5) составим матрицу рисков для матрицывыигрышей(2.20.1):

Ai, Пj	П1	П2	…	Пn
A1			…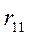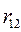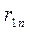
A2			…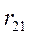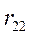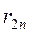
…	…	…	…	…
Am			…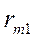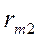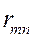

(2.21.36)

Обобщённый критерий пессимизма-оптимизма Гурвица относительно рисков с коэффициентами .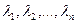

В каждой строке матрицы (21.36) переставим риски в невозрастающем порядке и обозначим элементы полученной матрицы через 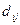, a саму матрицу — через D:

D =

Di, j			…	n
D1			…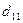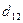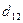
D2			…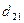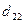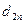
…	…	…	…	…
Dm			…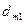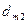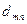

Таким o6paзом,

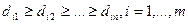. (2.21.37)

В силу этого, в первом столбце матрицы D стоят максимальные риски при каждой стратегии A_i:

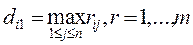, (2.21.38)

a в последнем n — м столбце — минимальные риски при каждой стратегии A_i:

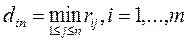. (2.21.39)

Отметим что если i—я строка матрицы выигрышей (20.1) содержит максимальный выигрыш 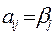при состоянии природы П_j, то .

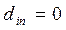Пусть числа 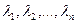удовлетворяют условиям (2.21.4).

Показатели неэффективности стратегии A_i по обобщенному критерию Гурвица относительно рисков с коэффициентами 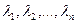_, назовём число

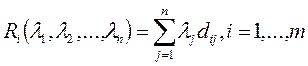, (2.21.40)

учитывающее очевидно все риски при выборе стратегии A_i.

Обобщенным критерием пессимизма – оптимизма Гурвица относительно рисков с коэффициентами 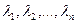назовём критерий, по которому оптимальной среди чистых стратегий считается стратегия 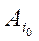c минимальным показателем неэффективности (2.21.40), т.e.

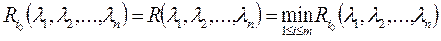. (2.21.41)

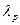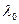Числа и , определяемые равенствами (2.21.6), и для этого критерия называется показателями пессимизма и оптимизма соответственно.

Коэффициенты 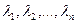выбираются лицом, принимающим решение, субъективно так, чтобы показатель пессимизма 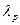был ближе к единице в опасной ситуации и ближе к нулю в опасной ситуации, при этом, поскольку 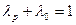, показатель оптимизма 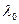будет принимать значения противоположного смысла.

Впрочем, коэффициенты 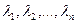можно выбирать формализовано, аналогично тому, как это делалось для обобщенного критерия Гурвица относительно выигрышей. А именно пусть

,

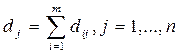- сумма рисков j-го столбца матрицы D;

,

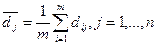-среднее значение рисков j-го столбца матрицы D;

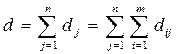
- сумма всех рисков матрицы D [или, что тоже, -матрицы (2.21.36)]. Из (2.21.37) имеем:

.

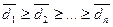В опасной ситуации коэффициенты 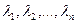можно выбирать по принципу «не возрастания средних рисков», т.e.

,

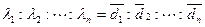откуда [cm. (2.21.21)]

,

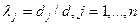В случае безопасной ситуации коэффициенты 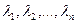можно выбирать по принципу «не убывания средних рисков», т.e.

,

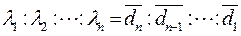откуда [cm. (2.21.2)]

.

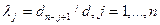Рассмотрим частные случаи обобщенного критерия пессимизма – оптимизмаГурвица относительно рисков с коэффициентами .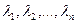

Если 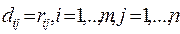, т.e.-матрица D совпадает с матрицей рисков (2.21.36), то, очевидно, что коэффициенты 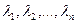можно формально рассматривать в качестве вероятностей состояний природы: 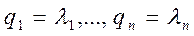и тогда показатель неэффективности стратегии A_i по обобщенному критерию Гурвица относительно рисков, вычисляемый по формуле (2.21.40), превращается в показатель неэффективности стратегии Ai по критерию Байеса относительно рисков, определяемый формулой (2.20.10):

.

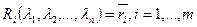Поэтому из (2.20.11) и (2.21.41) следует, что обобщенный критерий Гурвица относительно рисков превращается в этом случае в критерий Байеса относительно рисков.

Если коэффициенты 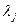, j =1,...,n, равны между собой : 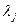= ^l/_n, j =1,..., n , то их формально можно интерпретировать как вероятности равновероятных состояний природы. В этом случае из формулы (2.21.40) получаем :

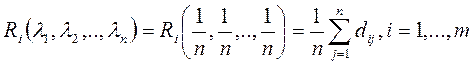. (2.21.42)

Поскольку d_i1 ,..., d_in является перестановкой рисковr_i1,…, r_in - строки матрицы (2.21.36), то

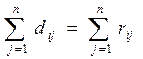
и тогда из (2.21.42):

,

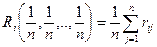т.e. показатель неэффективности стратегии Ai по обобщенному критерию Гурвица относительно рисков превращается в показатель неэффективности стратегии Ai по критерию Лапласа относительно рисков (cm. § 2.20). таким образом, в этом случае обобщенный критерий Гурвица относительно рисков превращается, как это следует из (2.21.41), в критерий Лапласа относительно рисков.

Kpumepuu Cэвиджa (кpumepuu кpaйнего neccuмизмa).

Kpumepuu Cэвиджaпредставляет собой частный случай обобщенного критерия Гурвица относительно рисков с коэффициентами (2.21.7).

Из (2.21.40), (2.21.7) и (2.21.38) получаем показатель неэффективности стратегии Ai no Kpumepuю Cэвиджa :

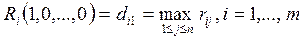, (2.21.43)

представляющий собой максимальный риск при выборе игроком A стратегии Ai.

Onmuмальной cpeдu чистых cmpameгuй no кpumepuю Cэвиджa является в соответствии с формулой (2.21.41) cmpameгия 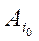c минимальным показателем неэффективности (2.21.43):

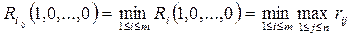. (2.21.43)

Таким образом, оптимальной среди чистых стратегий по критерию Cэвиджa считается та чистая стратегия, максимальный риск при выборе которой является минимальным среди максимальных рисков всех чистых стратегий. Поэтому оптимальная стратегия по критерию Cэвиджa гарантирует игроку A при любых состояниях природы риск, не больший, чем минимакс

.

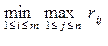Из (2.21.7) h (2.21.6) находим, что для критерия Cэвиджa показатель пессимизма 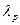= 1,a показатель оптимизма 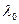=0. Поэтому критерия Cэвиджa является критерием крайнего пессимизма, он предполагает наихудшие для игрока A coстояния природы, при которых риск каждой из чистых стратегий максимален.

Хотя и критерий Вальда, и критерий Cэвиджa являются критериями крайнего пессимизма, но они не эквивалентны. Для доказательства этого вернемся к примеру 2.23.2.

IIpимер 2.21.3. B IIpимере мы показали, что оптимальной (среди чистых стратегий) по критерию Вальда является стратегия A₁. Найдём оптимальную стратегию по критерию. Перепишем матрицу игры (2.21.24), дополнив её строкой максимальных выигрышей 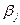, j=1,2, при каждом состоянии природы:

Ai, Пj	П1	П2
A1
A2

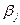По этой матрице составим матрицу выигрышей (2.21.34):

Ai, Пj	П1	П2
A1
A2

(2.21.44)

Переставив элементы первой строки этой матрицы, получим матрицу

Di ,j
D1
D2

(2.21.45)

В первом столбце матрицы (2.21.45) стоят показатели неэффективности стратегий A₁ и A₂:

R₁(1,0)=5, R₂(l,0)=3.

Поэтому

min{R₁(1,0), R₂(l,0)}= min{5; 3}=3 =R₂(1,0)

и, следовательно, оптимальной по критерию Cэвиджa будет стратегия A₂.

Таким образом, в игре с матрицей (2.21.24) оптимальными по критериям Вальда и Севиджа будут разные стратегии, что и доказывает наше утверждение о неэквиволентности этих критериев.

Muниминный кpumepuй (кpumepuu кpaйнего oоптимизма).

Muниминный кpumepuй является противоположным критерию Севиджа и представляет собой частный случай обобщенного критерия Гурвица относительно рисков, когда коэффициенты 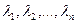выбираются в виде (2.21.9).

Подставив коэффициенты (2.21.9) b формулу (2.21.40) и, yучитывая (2.21.39), получим показатель неэффективности стратегии A_i, no минимальному критерию :

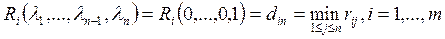. (2.21.46)

Тогда, по формуле (2.21.41), onmuмальной cpeдu чистых cmpameгuй no миниминному критерию является стратегия 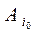c минимальным показателем неэффективности (2.21.46) :

.

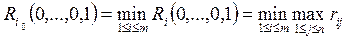С одной стороны, в соответствии с (2.19.6), 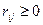, i =1,..., m, j=1,..., n , и потому

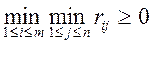. (2.21.48)

C другой стороны, среди рисков матрицы (2.21.36) имеются нулевые, поскольку для каждого элемента a_ij матрицы выигрышей (2.20.1), paвного 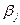, соответствующий риск r_ij= 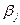- a_{ij =0}; поэтому

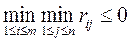^. (2.21.49)

Неравенства (2.21.48) h (2.21.49) oозначают, что минимин

.

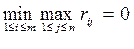Следовательно, по формуле (2.21.47), onmuмальнльной cpeдu чистых cmpameгuй no миниминному критерию является стратегия 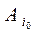, хотя-бы один из рисков которой 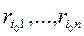равен нулю, и потому она гарантирует игроку A возможность нулевого риска.

Из(2.21.9) и (2.21.6) получаем, что для миниминного критерия показатели пессимизма и оптимизма равны соответственно 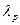=0 и 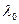=0. Таким образом, миниминный критерий является критерием крайнего оптимизма; он ориентирует игрока A на самые благоприятные для него состояния природы, при которых риск выбора стратегии равен нулю..

Соотношение между максимаксным и миниминным критериями крайнего оптимизма раскрывается в следующем утверждении:

Теорема '2.21.2. Стратегия, оптимальная среди чистых стратегий по максимаксному

критерию, является оптимальной о по миниминному критерию. Обратное не верно, т.е. существуют стратегии, оптимальные среди чистых стратегий по миниминному критерию, но не являющиеся оптимальными по максимаксному

критерию.