Метод регрессионного анализа

Прогнозируемое значение материального потока рассчитывается какзначение математической функции, наиболее точно описывающей изменение значений материального потока за несколько предыдущих периодов.

Приэтом способе прогнозирования используется метод наименьших квадратов, исходные положения которого приведены ниже.

Пусть имеется таблица данных:

По характеру расположения точек (х,;у|) установлено, что они располагаются условно на прямой у = ах + b (рис 2.1)

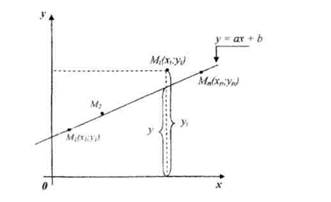
Сущность метода наименьших квадратов состоит в том. что искомую

прямую у = ах + b выбирают таким образом, чтобы сумма квадратов

отклонений угу была бы наименьшей.

Таким образом, неизвестные параметры а и b находятся из условия, что сумма

Y^b'i-yV или 2^Ь',-(от,+б)] имела наименьшее значение. Поскольку л-, у,

1-1 (=1

- постоянные числа, то указанная сумма есть функция двух параметров а и b :

S(a.bJ = ±b'-ia^.+b)]. (2.5)

Чтобы найти значения параметров а и Ь, воспользуемся необходимым условием экстремума функций двух переменных: найдем частные производные от 5 {а . Ь) по а и h и приравняем их к нулю

da ~г(

> = 2io',---*)(-l)^0 ^2.6)

da ^

ИЛИ

или

"Ё-т;-^''Z-'^. =Z''^-'''
< ';' '"■ ^ '-' (2.8)

Значения а и h найдем, решив систему методом определителей:

Z-VV, S-v,

a = -^-------------- = -^---------- '-^—'-^— (2.9)

±к Ь: "Zv-lZ-.)^

(=1

6 = _Ji------- ^z!----- _ = ^zi------- ;z!------- ^!------ ji_ (2.10)

Таким образом, цля определения а и b получили систему двух уравнений первой степени. Доказано, что система 2 имеет единственное решение, и что при найденных а и b функция S(a,b) имеет минимум. (Проверяются достаточные условия существования экстремума функции двух вариантов).

Подставляя найденные значения а » b в уравнение у = ах + Ь. получим линейную функцию, наилучшим образом отражающую зависимость между величинами х и у.

Теперь приведем пример определения прогнозируемого материального потока каждым из вышеперечисленных методов. В таблице 2.2 заданы размеры материальных потоков в соответствующие временные периоды.

Таблица 2.2
Изменение материального потока по годам
Годы, tI 2005 ' 2006 1 2007 1 2008 1 2009

Iviar. потокyVftj, тыс.т/год 45,15 57,13 'бзУГг" 67,30 78,10

1. Определение методом наивного прогноза.

В этом случае значение прогноза на Л',, /,, год составит: N(5ti)=N,5)=78,10 (тыс. т/год)

2. Расчет методом простого среднего.

Для исходных данных, приведенных в таблице 2.1, получим:

т,. 45.15 + 57.13+63.12 + 67.30+78,10 ,- .,, , ,

]\| 5 + 1 )=------------------------------------ — =62,1 6(ТЫС.Т/Т0Д)

3. Определение методом скользящего среднего.

Предположим, что эксперты присвоили следующие оценки весов: а,ц=ОЛ, «,;;=0.1, а(31=0,\5, о^^,=0,25, ap-j=0,4,

Расчет значения прогноза выполнен по формуле (2.3) при ограничении (2.4):

N|5-.;,=0,4-78,]+0,25-67,3+0,15-63,12-^0,1 57,] 3+0,1-45,15-

= 67,76 (тыс.т/год)

4. Определение методом регрессивного анализа.

В общем виде уравнение искомой функции может быть записано следующим образом:

Nm=F„:i^ (2.11)

где F,i, — значение функции в t-й год;

S — погрешность, показывающая величину отклонения

теоретических значений от -экспериментальных.

Функция может иметь любой вид: прямая, парабола и т.д. Выбор

функции, наиболее точно описывающей заданные изменения материального

потока, осуществляется на основании минимизахщи значения ногрещности д.

которое рассчитывается по формуле:

^ ,1^71^ (2.12)

где Л',„ — значение материального потока в t-й год (фактическое): и — число наблюдений;

р — число параметров в уравнении тренда (число неизвестных). Для анализа принимаем две функции: линейную и полином 2-го порядка:

f(t)=a+bt (2.13)

f,n)=a+bt+ct^ (2.14)

где a — начальный уровень тренда;

b — средний абсолютный прирост в единицу времени, константа

линейного тренда; с — квадратичный параметр равный половине ускорения, константа параболического тренда. Значения коэффициентов а, Ь, с определены с помощью метода нам.меньших квадратов.

Продифференцируем каждое уравнение и составим систему нормальных уравнений:

^ для линейного тренда:

■';' „ '" „ (2.15)

Z'\)-'. ="■£'.-*-Z'r

v^ для параболического тренда:

.=1 ,=i ,=1

■t-4i'.="I'.+*S'^^-S'- (2.16)

гИ ;=l .-1 ..1

_ ;=1 J=l J=l .=1

Для упрощения расчетов используем метод отсчета времени от условного начала. Обозначим в ряду изменения значений времени (/) таким

образом, чтобы 2^г, стала равна нулю.

Представим метод расчета и его результаты в виде таблицы:

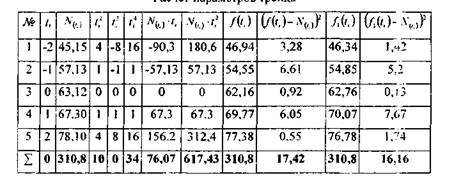Значения а п с найдем, решив систему методом определителей. Получаем: а = 62,76 , с = -0,3.

Рассчитанные значения fftj и fi(tj при t,=[-2;2]. и суммы квадратов азностей теоретических и практических значений приведены в табл.2.2

Дпя линейного тренда

_ I 17.42 _ _.

Так как 2,95<4,02 , линейный тренд является боле предпочтительной функцией, т.е. Ffy=f{t). В этом случае прогноз искомого параметра целесообразно определять по формуле линейного тренда, т.е. F^j=62,16+7.6-3=84,99(thc. т/год)

Графики N,„ и Ff„ приведены на рисунке 2.2.

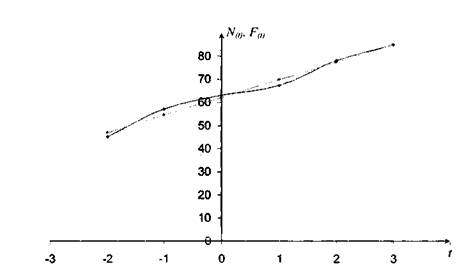
Итак, планируемый размер материального потока в 2010 году, определенный методом регрессионного анализа составляет 84 990 тонн.

3. Определение оптимального размера партии поставки.

Запасы играют как положительную, так и отрицательную роль в деятельности логистической системы. Положительная роль заключается в том, что они обеспечивают непрерывность процессов производства и сбыта продукции, являясь своеобразным буфером, сглаживающим непредвиденные колебания спроса, нарушение сроков поставки ресурсов, повышают надежность логистического менеджмента.

Негативной стороной созд<шия запасов является то, что в них иммобилизуются значительные финансовые средства, которые могли бы быгь использованы предприятиями на другие цели, например, инвестиции в новые технологии, исследования рынка, улучшение экономических показателей деятельности предприятия. Кроме того, большие уровни запасов готовой продукции препятствуют улучшению ее качества, так как предприятие, прежде всего, заинтересовано в реализации уже имеющейся продукции до вложения инвестиций в повышение ее качества. Исходя из этого, возникает проблема обеспечения непрерывности логистических и технологических процессов при минимальном уровне затрат, связанных с формированием и управлением различными видами запасов в логистической системе [14].

Один из методов эффективного управления запасами ~ определение оптимальных партий поставок груза, который позволяет оптимизировать расходы на транспортировку, хранение груза, а также избежать избытка или недостатка груза на складе.

Оптимальный размер партии поставки </ определяется по критерию минимума затрат на транспортировку продукции и хранение запасов.

Величина суммарных затрат рассчитывается по формуле (3.1);

С=С,„,+С\„ (3.1)

где С,,,,, — затраты на транспортировку за расчетный период (год), у.е.;

Cv,, — затраты на хранение запаса за расчетный период (год), у.е. Величина С^, определяется по формуле:

где п — количество партий, доставляемых за расчетный период,

Сщр — тариф на перевозку одной партии, у.е./партия. Затраты на хранение определяются по формуле (3.4):

C\,,=qcr-c^p (3.4)

где c/^j, — средняя величина запаса (в тоннах), которая определяется из предположения, что новая партия завозится после того, как предыдущая полностью израсходована. В этом случае средняя величина рассчитывается по следующей формуле:

44,=q/2 (3.5)

Подставив выражения С,„р и С,„р в формулу (3.1), получим:

ч ^

функция общих затрат С имеет минимум в точке, где ее первая производная по q равна нулю, т.е.

f —-^-Т^" (3.7)

Решив уравнение (3.7) относительно с/ получим оптимальный размер партии поставки:

в качестве размеров годового объема потребления продукции принимаем данные, полученные в результате прогнозирования методом простого среднего: Q=62,\6 тыс. т/год; тариф на перевозку одной партии Стр=50 у.е./т; расходы, связанные с хранением запаса Схр=]Оу.е./т.

Подставив заданные значения, получим:

|2*62160*50 „- .. , ,

о = , = 788.42 (т)

V 10 ^

При этом общие затраты составят:

788,42 2 "

Решение данной задачи графическим способом заключается в

построении графиков зависимости C„p(q), C^^/q) и CfqJ ,предварительно

выполнив необходимые расчеты по определению С,„р, Сур и С.

Определим значения С„,„ Сур и С при изменении q в пределах от 600 до

1000 с шагом 100. Результаты расчетов занесем в табл.3.1.

Таблица 3.1

Значения С„р, С^р и С

^~~~---J»a3Mep партии, о I

^~^-^^ 600 700 800 900 1000

Затраты, у.е. "^"^-^.^^^

С„р 5180 4440 3885 3454 3108

С^р 3000 3500 4000 450(Г 5000

С STSCT 7940 Т885 7954 8108

По данным табл.3.1 построены графики зависимости затрат (транспортных, складских и суммарных) от размера партии (рис.3.1).

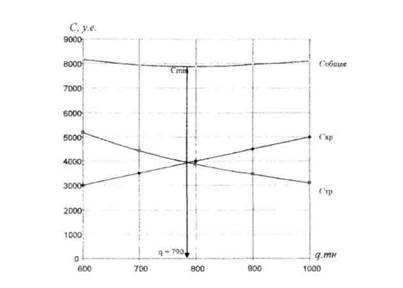
Анализ графиков на рис.3.1 показывает, что затраты на транспортировку уменьшаются с увеличением размера партии, что связано с уменьшением количества рейсов. Затраты, связанные с хранением, возрастают прямо пропорционально размеру партии.

График суммарных затрат имеет минимум при значении q приблизительно равном 790 т, которое и является оптимальным значением размера партии поставки. Соответствующие минимальные суммарные затраты составляют 7885 у.е.

Произведем расчет оптимального размера партии в условиях дефицита при величине расходов, связанных с дефицитом С()еф=]5 у.е/т.

в условиях дефицита значение q*, рассчитанное по формуле (3.8) корректируется на коэффициент к, учитывающий расходы, связанные с дефицитом.

. =А.^--_ (..9)

Коэффициент к рассчитывают по формуле (3.10);

<=J-^^^ (3.10)

Сдеф - величина расходов, связанных с дефицитом; принимаем Сдеф=\5у.е.1-г Подставив значения, получим:

g = 1.29*788.42 = 1017 (т)

Из этого следует, что в условиях возможного дефицита размер оптимальной партии поставки при заданных условиях необходимо увеличить на 29%.