Технологии решения задач по скалярному критерию

Предположим, что в некоторой проблемной ситуации удалось обойти трудности, указанные для общей постановки задачи обоснования решений. Тогда мы сможем преобразовать исходную задачу, заданную выражением (2.1), в задачу математического программирования вида:

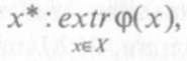
где extr (р(х) — экстремум (максимум или минимум) заданной скалярной функции w>(х) векторного аргумента х.

Среди подобных проблемных ситуаций в практике управления часто встречаются следующие задачи принятия решений:

• составление оптимального плана транспортировки материальных средств;

• определение кратчайших маршрутов на заданной транспортной сети;

• принятие решений об оптимальной загрузке транспортных средств грузами;

• принятие решений о назначении исполнителей для выполнения работ какой-то целостной программы или проекта и др.

Как правило, все перечисленные задачи являются задачами дискретного математического программирования[6,7].

Рассмотрим математические постановки и представим общие описания технологий решения подобных задач.

Задача составления оптимального плана транспортировки материальных средств. Рассмотрим эту задачу (применительно к ее простейшему случаю — транспортировке однотипных материальных средств, которые могут быть разделены на части произвольным образом. Например, такими материальными средствами мы можем считать комплекты одежды, горючесмазочные материалы (ГСМ), продовольственные товары в мелкой расфасовке, различные комплектующие изделия и т. п. А вот оптимизировать план перевозки крупногабаритных грузов, например, тяжелой автомобильной или железнодорожной техники, которую можно везти только целиком, которую нельзя разделить на части (т. е. "неделимые" объекты), в рамках рассматриваемой задачи нельзя.

Вербальная постановка задачи планирования перевозки однотипных "делимых" грузов на примере обеспечения потребителей ГСМ выглядит следующим образом. ГСМ располагаются на нескольких складах поставщика. Известны расположение складов и запасы ГСМ на них. Известен отдельный спрос потребителей в ГСМ, а также характеристики дорожной сети в регионе. К числу характеристик дорожной сети отнесем протяженности отдельных участков дорог, типы дорожных покрытий, грузоподъемности мостов и переправ и др. Тактико-технические характеристики автоцистерн известны.

Требуется составить план перевозок, отвечающий следующим требованиям:

• удовлетворение потребностей (заявок) всех клиентов, если имеются соответствующие запасы ГСМ на складах;

• частичное удовлетворение заявок клиентов в соответствии с их приоритетами, если на складах нет ГСМ в достаточном количестве;

• стремление обеспечить рациональность плана — т. е. как можно больший эффект, как можно меньшие затраты и время на перевозки.

Конкретный смысл понятия "рациональности" плана зависит от условий решения поставленной задачи. Так, например, если перевозки планируют проводить при определенном дифиците времени, то рациональность плана может быть выражена уменьшением суммарного пробега автоцистерн, экономией топлива на перевозку и т. п.

Рациональность плана может быть обеспечена стремлением минимизировать скалярную целевую функцию, интерпретируемую как "суммарная цена перевозки". Эта суммарная цена, так или иначе, вычисляется через результаты, характеризующие перевозку единицы массы ГСМ с какого-то склада в адрес конкретного потребителя. В свою очередь, упомянутые результаты рассчитываются через значения частных- компонентов концептуальных критериев "Эффекта", "Затрат" и "Времени". Например, для обычных условий нашего времени рациональность чаще всего отождествляют со стремлением уменьшить суммарный пробег автоцистерн; для условий форсмажорных обстоятельств рациональными обычно считают варианты, обеспечивающие наивысшую оперативность выполнения поставленных задач.

Технология оптимизации плана перевозки в рамках представленной вербальной постановки задачи включает:

• формирование математической постановки задачи и приведение ее к каноническому ("сбалансированному") виду;

• применение алгоритма для решения канонической транспортной задачи;

• интерпретацию полученного оптимального решения канонической задачи и принятие решения относительно наилучшего способа реализации плана транспортировки.

В качестве примера реализации технологии рассмотрим "транспортную задачу" для обычных условий. Для формирования математической постановки задачи обозначим:

m , i — число складов ГСМ и номер склада, соответственно;

n, j — число клиентов, заказавших ГСМ (в дальнейшем именуются "потребителями"), и номер потребителя, соответственно;

b_j — количество ГСМ, нужное j-му потребителю;

аᵢ — запас ГСМ на i-м складе;

lᵢ_j расстояние между i-м складом и j-м потребителем (длина маршрута, по которому может перевозиться ГСМ в адрес j-го потребителя с i-гo склада);

vᵢ—допустимая грузоподъемность автоцистерн, используемых при перевозках с i-гo склада;

хᵢ_j, — количество ГСМ, перевозимое с i-гo склада к j-му потребителю.

Если не учитывать ограничения на целочисленность числа поездок, то при использовании цистерн грузоподъемностью v_i, нужно будет сделать х_ij/v_i поездок. В этом случае средний пробег автоцистерны составит величину 2*lᵢ_j* хᵢ_j/ v_i. Обозначим величину 2*lᵢ_j / v_i через с_ij, и будем рассматривать ее как "стоимость" перевозки единицы ГСМ с i-го склада j-му потребителю, а матрицей | х_ij| будем обозначать план перевозок. В таком случае суммарная "стоимость" всех перевозок ГСМ при выбранном плане | х_ij| перевозок составит величину

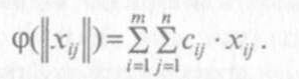(2.3)

Естественные ограничения на реализуемость плана выглядят следующим образом:

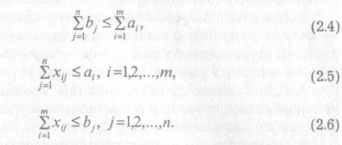
Канонической ("сбалансированной") транспортной моделью называется такая, у которой ограничения, задаваемые выражениями (2.4) и (2.5), являются ограничениями-равенствами. Приведение задачи к каноническому виду осуществляют либо путем введения в рассмотрение дополнительного фиктивного потребителя с объемом фиктивной заявки, точно равным избыточному запасу на складах, либо введением фиктивного склада с объемом запаса в размере недостающей поставки. В обоих случаях принимают нулевую стоимость перевозок с фиктивного "склада" или в адрес фиктивного потребителя.

Алгоритм решения канонической транспортной задачи реализуется как пошаговый (говорят — "итерационный"). Оформляются итерации в виде отдельных расчетных таблиц. На начальном шаге алгоритма составляют таблицу, число строк которой равно числу складов, а число столбцов — числу потребителей. Заголовками строк и столбцов являются объемы аᵢ запасов и b_j, потребностей соответственно. В каждой ячейке таблицы записывают величины соответствующих цен с_ij. Затем составляют любой план (его называют "опорный"), который удовлетворяет ограничениям задачи. Значения компонентов x_ij, характеризующих объемы перевозок груза по опорному плану, размещают в ячейках рядом с величинами с_ij цен перевозок. Лучше, разумеется, найти такой опорный план, который является как можно больше похожим на оптимальный. Тогда будет меньше последующих итераций. Очень хорошее приближение дает опорный план, найденный по алгоритму Фогеля, состоящему из следующих шагов:

1. Для каждой строки таблицы упорядочить элементы цен перевозок с_ij по возрастанию. Вычислить величину так называемого штрафа строки как разность значений второго и первого элементов в ранжированном ряду.

2. Для каждого столбца таблицы упорядочить элементы цен перевозок с_ij по возрастанию и вычислить величину "штрафа столбца" аналогично шагу 1.

З. Найти строку или столбец, имеющую (имеющий) наибольший штраф по всем штрафам строк и столбцов, а в ней (в нем) — элемент с минимальной величиной стоимости перевозок с_ij. Зафиксировать индексы (i, j) этого элемента.

4. Присвоить переменной х_ij, индексы которой соответствуют шагу 3, наибольшее из допустимых для нее значений (с учетом ограничений задачи).

5. Скорректировать величины а_i и b_j и вычеркнуть строку i, если оказалось, что а_i = 0, или столбец j, если b_j = 0.

6. Проверить, все ли величины а_i, и b_j равны нулю. Если да, то окончить вычисления; в противном случае взять в качестве исходной оставшуюся часть таблицы и перейти к шагу 3 алгоритма.

Затем производят итерации, направленные на улучшение найденного приближенного решения задачи, вплоть до получения оптимального плана[7].

По достижении оптимального плана алгоритм останавливается. Может получиться, что оптимальных планов несколько. Тогда необходимо провести содержательный анализ различий в найденных оптимальных решениях и выбрать тот вариант плана, который является более предпочтительным. Завершает решение задачи интерпретация полученного оптимального варианта с целью конкретно назначить кому, что, где, как и с помощью чего перевозить и по каким маршрутам.

Задача определения кратчайших маршрутов на заданной транспортной сети. Следует заметить, что для минимизации целевой функции (р{\х.}\) в транспортной задаче нужно, чтобы "стоимости" с.., входящие в выражение (2.3) для нее, уже были бы минимальны. Таким образом, возникает еще одна оптимизационная задача, связанная с отысканием "кратчайшего" маршрута L o t г-го склада до j-гo потребителя на заданной дорожной сети. Рассмотрим постановку этой задачи. Дана матрица |dj длин участков дорожной сети, соединяющих узлы с номерами s и t. Если между какими-либо узлами дорожной сети нет прямого сообщения, то на соответствующем месте в матрице ничего не проставлено. Заметим, что элемент dst в общем случае может отличаться от элемента dts в силу, например, одностороннего движения в том или ином направлении. Требуется определить кратчайший маршрут между узлом s и каким-либо другим узлом t

Для решения задачи исходные данные заносят в матрицу. Далее применяют или алгоритм Беллмана динамического программирования, или метод Дейкстры, который является его модификацией. Эти алгоритмы весьма просты, и справку по ним можно найти, например, в справочнике[7].

Если требуется транспортировать грузы, которые нельзя разделить на части ("неделимые" объекты), приходится решать задачу об оптимальной загрузке транспортных средств грузами с учетом их веса, габаритных размеров и ценности (или важности). В теории каноническая форма такой задачи получила название "задача о ранце". Эту задачу также решают по алгоритму Беллмана. Сразу отметим, что частным случаем "задачи о ранце" является задача о назначении исполнителей для выполнения работ в рамках некоторой целостной программы или проекта, и хотя подобную задачу также можно решить методом Беллмана, обычно применяют более эффективные, специальные алгоритмы. Рассмотрим подробнее постановку и удобный графический алгоритм решения задачи о назначении.

Дано: m, i - число исполнителей и номер исполнителя для выполнения работ;

n,j - число работ и номер работы;

с_ij - затраты на выполнение j-й работы i-м исполнителем.

Требуется: Найти распределение исполнителей по работам (один исполнитель строго на одну работу) так, чтобы минимизировать суммарные затраты на производство работ.

Если принять "объем запаса" на каждом складе равным единице и "объем спроса" у каждого потребителя равным единице, то описанная задача о назначении в точности совпадает с постановкой транспортной задачи. Поэтому, если наблюдается дисбаланс, т. е. m≠n, то добавляют фиктивные работы или фиктивных исполнителей, поэтому далее без потери общности будем считать, что задача сбалансирована в вышеуказанном для транспортной задачи смысле.

Следует отметить, что сформулированная задача о назначении обладает интересной особенностью, а именно: оптимальное решение не изменится, если к любому столбцу или к любой строке матрицы |c_ij| исходных данных прибавить постоянное число.

Пусть, например, величины р_i и q_j вычитаются из i-й строки и j-го столбца соответственно. В этом случае новые "затраты" будут описываться матрицей |d_ij| с элементами d_ij = c_ij – р_i – q_j , а новая целевая функция определится соотношениями:

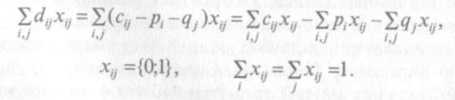
Видно, что новая целевая функция отличается от исходной лишь на константу и, следовательно, минимизация новой целевой функции приводит к минимуму исходной. Возникает вопрос: а что это все нам дает? Практически все методы решения задачи о назначении в той или иной степени основаны на использовании указанного свойства задачи о назначении.

Если размерность задачи невелика, число работ (или работников) не превышает 15—20, то поиск решения удобно проводить графоаналитическим методом. Он основан на том, что, если на основе исходной матрицы цен удастся построить новую матрицу, в которой будут содержаться такие нулевые элементы, совокупность которых будет образовывать допустимое решение, то после формирования плана путем записи единиц в матрице | x . J на места, занимаемые указанными нулевыми элементами, получим оптимальное решение. Это действительно так, поскольку элементы е.. по смыслу — затраты, которые, конечно же, не могут быть отрицательными.

Алгоритм графоаналитического метода работает следующим образом:

1. Для каждой строки выполняют следующие действия: находят в ней наименьший элемент и вычитают его из каждого элемента строки; в результате в каждой строке получается хотя бы один нуль.

2. Если в каждой строке оказалось по одному нулю, то получено оптимальное решение; Stop.

3. Если полученное решение еще не оптимально, то проводят минимальное число прямых линий через некоторые строки и столбцы так, чтобы все нули оказались вычеркнуты.

4. Выбирается наименьший невычеркнутый элемент, который вычитается из каждого невычеркнутого элемента и прибавляется к каждому элементу, стоящему на пересечении проведенных прямых.

5. Перейти к п. 2.

6. Stop.

Рассмотрим пример применения представленного алгоритма

для матрицы затрат следующего вида:

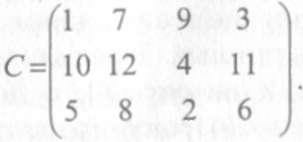
Приведем задачу к сбалансированному виду. Для этого добавляем четвертого, фиктивного, исполнителя с весьма значительной ценой выполнения всех работ. Например, каждую из всех его «услуг» оцениваем в 100 единиц. Получим новую матрицу С’ цен работ, представленную на рис 2.4, а.

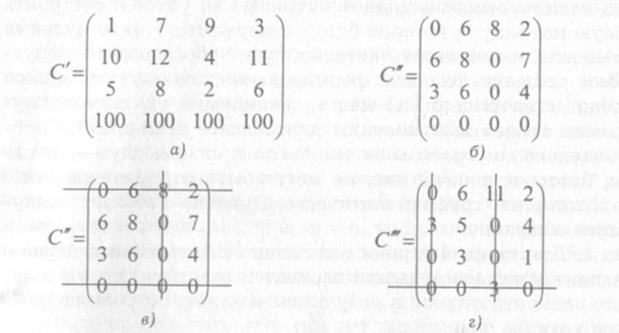
Рис. 2.4. Этапы преобразования матрицы цен

Преобразуем эту матрицу согласно алгоритму. Из каждой строки матрицы С’ вычитаем наименьший в этой строке элемент. Получим матрицу С’’, изображенную на рисунке 2.4, б. В образовавшейся матрице строк или столбцов, которые не содержали бы нулей, нет, и, следовательно, пока получить допустимое решение из нулевых элементов не получается. Поэтому вычеркиваем образовавшиеся нули минимальным числом прямых линий. Например, как это сделано на рис 2.4, в. Находим среди невычеркнутых элементов последней матрицы наименьший. Это элемент c₃₁ = 3. Вычитаем элемент c₃₁ из всех невычеркнутых элементов матрицы С’’ и прибавляем его значение к значениям всех элементов, стоящих на пересечении прямых. В результате получаем матрицу С’’’, представленную на рис. 2.4, г. Допустимого решения по-прежнему еще нет. Поэтому продолжаем вычеркивание (показано на матрице). Наименьший из невычеркнутых элементов равен 1. Вычитаем его из всех невычеркнутых элементов матрицы С”” и прибавляем к элемента, находящимся на пересечении прямых. Образовавшаяся матрица C_итог, представленная ниже, содержит совокупность нулей, удовлетворяющих ограничениям задачи:

Таким образом, план х* наилучшего назначения имеет вид:

х₁₁ = 1; x₂₃ = 1; x₃₄ = 1; x₄₂ = 1.

Однако четвертый «работник» - фиктивный, поэтому реально вторая работа исполняться не будет. Общие затраты на исполнение трех работ из четырех соответственно составляет:

(c₁₁ = 1) + (c₂₃ = 4) + (c₃₄ = 6) = 11

Графоаналитический метод трудно записать в виде программы ЭВМ в силу трудности формализации пожелания «зачеркнуть нули минимальным количеством прямых». Поэтому если размерность задачи большая и требуется процесс оптимизации автоматизировать, чаще всего применяют метод Мака. Он также основан на идее выбора в каждой строке минимального элемента. Чтобы распределить элементы по строкам и столбцам, здесь также используется идея сложения или вычитания одного и того же значения со всеми элементами строк и столбцов. По-прежнему будет рассматриваться уже сбалансированную задачу, пользуясь понятиями «невыбранного» - М1 и «выбранного» - М2 подмножеств столбцов платежной матрицы.

Алгоритм включает выполнение следующих шагов:

1. Найти в каждой строке минимальный элемент и подчеркнуть его.

2. В каждом столбце оказался только один подчеркнутый элемент? Если да, то перейти к пункту 12 – «Stop».

3. В множество М1 «невыбранных» столбцов записать все столбцы исходной матрицы «С».

4. Из М1 выбрать столбец М1(J), в котором более одного подчеркнутого элемента, и включить его во множество М2 «выбранных» столбцов.

5. Для всех строк, имеющих во множестве М2 подчеркнутые элементы, вычислить разности между минимальными из элементов множества М1 в данной строке и этими подчеркнутыми элементами. Обозначим эти разности через Di.

6. Определить минимальный из элементов D* по п. 5 и прибавить эту величину ко всем элементам множества М2.

7. В строке, соответствующей минимальному элементу по п. 5, найти элемент С(r, k),обеспечивающий эту минимальную разность, и подчеркнуть его пунктиром; зафиксировать номера r строки и k столбца, на пересечении которых стоит подчеркнуты пунктиром элемент. Если строк, обеспечивающих величину минимальной разности несколько, то берется та r строка, элемент которой (обеспечивающий величину D*) стоит в столбце, не содержащем ни одного подчеркнутого элемента.

8. Проверить, есть ли в столбце М1(k), в котором находится элемент С(r, k), хотя бы один подчеркнутый элемент. Если да, то включить столбец М1(k) во множество М2 и перейти к п. 5.

9. Подчеркнуть элемент С(r, k) сплошной линией, найти ранее подчеркнутый элемент в той же строке r и убрать подчеркивание.

10. Проверить, содержится ли в столбце, в котором только что убрали подчеркивание, отмеченный пунктиром элемент. Если да, то обозначить этот элемент С(r, k) и перейти к п. 9.

11. Проверить, есть ли столбцы без подчеркнутых элементов. Если да, то перейти к п. 3.

12. Stop.

Проиллюстрируем применение метода Мака на ранее рассмотренном примере. Матрица цен имеет тот же вид, но мы ее повторили на рис. 2.5, а.

На первом шаге все столбцы «невыбранные», поэтому М1 = С. Подчеркиваем минимальные элементы строк в матрице С, как это сделано на рис. 2.5, б. Замечаем, что третий столбец содержит два подчеркнутых элемента. Включаем этот столбец во множество М₂ «выбранных» столбцов. Во множестве М₁ остаются 1,2 и 4-й столбцы матрицы С. Вычисляем величины D_2и D₃ в строках, где М2 стоят подчеркнутые элементы. Минимальной является разность D₃ = 3, которая получена для элемента с₃₁. Прибавляем D₃ ко всем элементам множества М2, подчеркиваем двойной чертой элемент, стоящий в третьей строке первого столбца, и получаем матрицу, представленную на рис. 2.5, в. В первом столбце уже был ранее подчеркнутый элемент (в первой строке первого столбца), поэтому включаем первый столбец во множество М2 «выбранных» столбцов. Теперь вычисляем разности D₁,D₂ и D₃ для всех трех строк матрицы (так как во всех строках множества М2 теперь есть подчеркнутые элементы). Это действие также схематично отображено на рис. 2.5, в. Минимальная разность D₃ = 1 достигается на элементе 3,4. Поэтому данный элемент(он равен 6) подчеркиваем двойной чертой.

Во 2-м столбце нет другого подчеркнутого элемента, поэтому подчеркиваем этот элемент 4,2 одной чертой, снимаем подчеркивание в этой строке с других элементов (с элемента (4,4). Мы сняли подчеркивание с элемента 4,4. Но в 4-м столбце, где элемент 4,4 находится (см. рис. 2.5, в), есть уже ранее подчеркнутый двойной чертой элемент 3,4. Раз теперь это подчеркивание в 4-м столбце единственное, то подчеркивание двойной чертой заменяем подчеркиванием одной чертой.

Контролируем наличие других подчеркиваний теперь уже в 3-й строке. В этой 3-й строке снимаем два ранее поставленных подчеркивания (двойной чертой был выделен элемент 3,1 и одной чертой был ранее подчеркнут элемент 3,3). Теперь оказывается, что подчеркиваний двойной чертой нет, а в каждом столбце только по одному подчеркнутому одной чертой элементу. Эти элементы находятся в позициях 1,1; 4,2; 2,3 и 3,4 матрицы. Учитывая, что 4-я строка матрицы — "фиктивный" работник, получаем оптимальный план назначения, как и при использовании графоаналитического метода.

Пример: Например, руководитель автотранспортного предприятия не уверен, что аварии будут, а если и будут – на какую сумму. Но из статистики известно, что каждый десятый водитель попадает раз в год в аварию. Также известно, что средняя сумма ущерба от одной аварии – 2000 долларов. Имея парк из 100 машин, руководитель может принять решение, что в аварию попадут 10 машин и общий ущерб составит около 20000 долларов и, следовательно, примет решение о страховании на такую сумму.