Усовершенствованный метод Эйлера

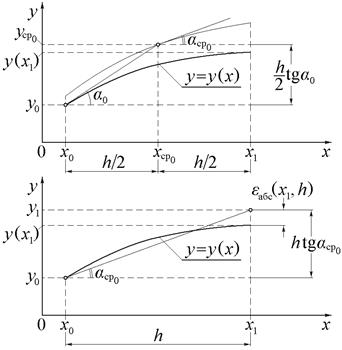
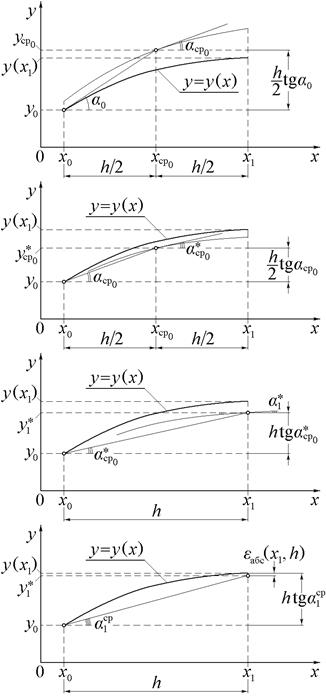
Характерной особенностью метода является использование в качестве направления поиска каждой последующей точки численного решения касательной, определяемой в центре отрезка [x_k, x_k+1]. Как видно на рис.4 для k = 0, последовательно выполняются два шага по методу Эйлера.

Первый из них используется для вычисления тангенса угла наклона касательной в средней точке отрезка [x_k, x_k+1]

,

,

,

.

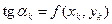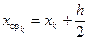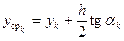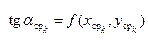После этого делается второй шаг – для вычисления новой точки

,

.

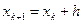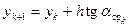Если тангенсы углов наклона касательных заменить на правую часть дифференциального уравнения f(x, y), то вышеприведенные фор­мулы для выполнения одного шага по усовершенствованному методу Эйлера сведутся к следующим

, ,

, .

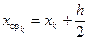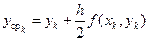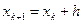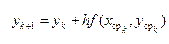Этот метод является методом второго порядка точности. Он даёт меньшую погрешность численного решения на шаге h, чем метод Эйлера. Его абсолютная погрешность ε_абс(x_k+1, h) на каждом шаге пропорциональна величине h³, а решение совпадает с истинным в случае, когда оно представимо квадратичной функцией y = a₁+ a₂x + a₃x². Однако это достигается тем, что его трудоёмкость увеличивается примерно в два раза, поскольку для одного шага приходится два раза вычислять значение правой части дифферен­циального уравнения.

Метод Рунге–Кутта (C.Runge 1895, W.Kutta 1901)

Под наименованием «метод Рунге–Кутта» принято подразумевать целое семейство методов численного решения задачи Коши, объединенных одной идеей выбора некоторого усреднённого направления поиска каждой новой точки приближённого решения. Алгоритм одного из этих методов: метода Рунге–Кутта 4-го порядка, строится по следующей схеме. Из начальной точки, как это можно видеть на рис.5 для k = 0, в направлении касательной делается шаг по методу Эйлера на величину h/2 и в полученной точке вычисляется тангенс угла наклона касательной

,

, ,

.

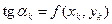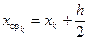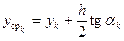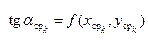Из начальной точки по найденному направлению делается второй шаг на ту же величину и определяется тангенс угла наклона во второй средней точке

,

.

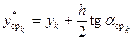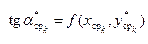Третий шаг делается опять из начальной точки по последнему найденному направлению ( 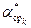), но на шаг h, где опять находится тангенс угла наклона касательной

,

,

.

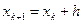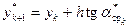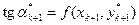Последний шаг из начальной точки на величину h делается по присущему этому методу осреднённому направлению и находится ордината следующей точки приближённого решения

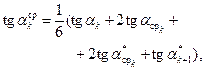
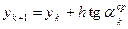
Описанные действия, необходимые для получения координат каждой последующей точки приближённого решения, реализуются в виде следующей последовательности вычислений по формулам

, ,

,

, ,

.

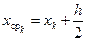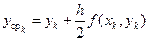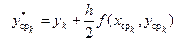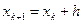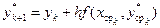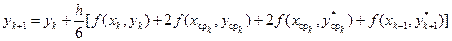Получающееся численное решение имеет на каждом шаге h погрешность ε_абс(x_k+1, h), которая пропорциональнавеличине h⁵. Оно совпадает с истинным решением в случае, когда оно – многочлен четвёртого порядка y = a₁+ a₂x + a₃x²+ a₄x³+ a₅x⁴.