Вторая позиционная задача (построение линии пересечения двух поверхностей)

Две поверхности пересекаются по линии (совокупности линий), которая одновременно принадлежит каждой из них.

В зависимости от вида и взаимного положения поверхностей линия их пересечения может быть прямой, плоской или пространственной ломаной, плоской или пространственной кривой.

Построение этой линии (независимо от ее формы) сводится к построению ряда точек, одновременно принадлежащих каждой из пересекающихся поверхностей (рис. 56).

Рис.56

Линия, в определенном порядке соединяющая эти точки, и будет искомой.

Основным способом построения точек, принадлежащих искомой линии пересечения, является способ вспомогательных поверхностей.

Сущность его заключается в том, что каждая из искомых точек рассматривается как результат пересечения двух линий, одна из которых является линией пересечения вспомогательной поверхности с одной из заданных, а вторая - линией пересечения той же вспомогательной поверхности с другой из заданных поверхностей.

В соответствии с этим построение произвольных точек 1 и 2, принадлежащих линии l пересечения поверхностей Ф и (независимо от их вида), осуществляется по следующей общей схеме (рис. 57):

Рис. 57

1. Проводится вспомогательная поверхность Σ, пересекающая заданные поверхности Ф и Ψ.
2. 2. Определяются линии m и n пересечения вспомогательной поверхности с каждой из заданных.
3. 3. Отмечаются точки 1 и 2 пересечения построенных линий m и n, которые и являются искомыми, так как одновременно принадлежат данным поверхностям Ф и Ψ, следовательно, линии l их пересечения.

В символической записи схема имеет вид:
1) Σ∩ФÙΨ ;
2) m = Σ∩ФÙ n = Σ∩Ψ;
3) 1 = m ∩ n Ù 2 = m ∩ n.

Выбор вида и положения вспомогательных поверхностей определяется в основном тремя соображениями:

1. Необходимо определить положение целого ряда опорных точек линии пересечения.

2. Любая из проведенных вспомогательных поверхностей должна пересекать каждую из заданных по таким линиям, проекций которых были бы, как правило, графически простыми линиями, т. е. прямыми или окружностями.

3. Все вспомогательные поверхности должны пересекать заданные в пределах зоны возможного расположения линии пересечения, чтобы избежать лишних построений.

МЕТРИЧЕСКИЕ ЗАДАЧИ

Метрическими называются задачи, связанные с измерением расстояний и углов.

В них определяются действительные величины и форма геометрических фигур, расстояния между ними и другие характеристики по их метрически искаженным проекциям.

Решение метрических задач основано на том, что геометрическая фигура, принадлежащая плоскости, параллельной плоскости проекций, проецируется на нее в конгруэнтную ей фигуру (см. аксиомы параллельного проецирования).

Поэтому при решении метрических задач широко используются способы преобразования комплексного чертежа, а также теоретические положения, изложенные в теме "Взаимно перпендикулярные прямые и плоскости".

В данной главе рассматриваются три группы метрических задач. К первой относятся задачи, в которых требуется найти расстояние между двумя геометрическими фигурами; ко второй - задачи на определение действительных величин плоских фигур и углов; к третьей группе принадлежат задачи, связанные с построением в плоскости общего положения геометрических фигур по заданным размерам.

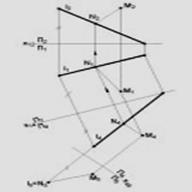Определение расстояния от точки М до прямой 1 общего положения (рис 58).

Рис.58

Искомое расстояние измеряется длиной отрезка /МN/ перпендикуляра, опущенного из точки М на прямую l.

Отрезок [МN] проецируется в конгруэнтный ему отрезок на плоскость проекций, перпендикулярную прямой l.

Алгоритм решения:
1. Преобразовать прямую l в проецирующую прямую способом замены плоскостей проекций.
2. Построить проекцию отрезка [МN] на плоскость П5^ l, длина которого определяет искомое расстояние.

Построение.Для преобразования прямой l общего положения в проецирующую выполнены две последовательные замены плоскостей проекций: вначале прямая l преобразована в линию уровня, затем линия уровня преобразована в проецирующую прямую. Построены проекций М4 и М5 точки М в системе П4/П5. Отрезок [М5N5] является искомым: [М5N5]@ [МN] и /М5N5/ = /МN/.

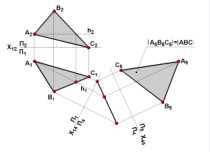Определение действительной величины плоской фигуры (рис.59).

Рис. 59