Модель задачи оптимального ассортимента продукции

Вычислительному процессу оптимизационных задач предшествует построение математической модели и наполнение ее соответствующей информацией. Математическая модель, имея символическое содержание, определяет необходимый объем информации для полноценного решения задачи.

В качестве плановой информации используются показатели работ предприятия и его подразделений на соответствующий плановый период (план выпуска продукции, план по труду и заработной плате, план использования производственных мощностей, материально-сырьевых, энергетических, финансовых и других ресурсов). Эти показатели обычно изменяются во времени и зависят от существующей системы планирования.

Учетно-отчетная информация – это фактические показатели, которые характеризуют производственно-хозяйственную деятельность предприятий и отражают его конкретные организационно-технические условия (выполнение планов выпуска продукции, объем реализации, отчетная себестоимость продукции, фактическое выполнение норм и т.д.).

Для математической записи оптимизационной ассортиментной задачи используем следующий небольшой пример. В цехе пищевого предприятия вырабатывается три вида продукции П₁, П₂, П₃. Известны виды используемых ресурсов в процессе производства P₁, P₂, Р₃, нормы расхода их на единицу готовой продукции и наличие каждого ресурса. В качестве критерия оптимальности принята прибыль на единицу каждого вида продукции. Численная информация задачи представлена в табл.4.

В качестве искомых неизвестных принимаются x₁, x₂, x₃, означающие количества включаемых в план производства видов продукции соответственно П₁, П₂, П₃.

Общий расход каждого ресурса на выпуск трех видов продукции не должен превышать наличие этих ресурсов. Это условие записано системой неравенств.

Математическая модель задачи оптимального ассортимента продукции содержит три составные части.

Первая часть – это, как правило, система неравенств, отражающих ограничения, которые содержатся в условии задачи. В общем случае модель имеет столько неравенств (или уравнений), сколько ограничивающих экономических факторов учитывается в данной задаче. Вторая часть модели включает условие неотрицательности значений переменных величин, которое является очевидным, но с математической точки зрения этот момент очень важен и поэтому обязательно отражается в модели. Третья часть – это уравнение, характеризующее поставленную в задаче цель. В данном случае речь может идти о доведении суммарной прибыли до максимального значения.

Математическая формулировка задачи оптимального ассортимента такова: определить значения неизвестных x₁, х₂, х₃ удовлетворяющие ограничениям, выраженным системой неравенств и равенств и обеспечивающие максимальное значение целевой функции, выраженной уравнением для определения ограничительных ресурсов.

Таблица 4

Виды основных ресурсов	Расход ресурсов на 1т продукции, т	Наличие ресурсов, т
П1	П2	П3
P1	0,3	0,4	0,1
P2	0,2	0,1	0,3
Р3	0,4	0,3	0,1
Прибыль на 1т, руб.

Предприятие располагает определенным количеством ресурсов (P₁, P₂, Р₃), общий расход которых на производство трех видов продукции не должен превышать заданных величин:

0,3x₁ + 0,4x₂ + 0,1x₃< 200

0,2x₁ + 0,1х₂ + 0,3х_з < 303

0,4x₁ + 0,3x₂ + 0,1x₃< 270

Выпуск продукции не может быть отрицательным, поэтому

х₁ ≥ 0, х₂ ≥ 0, х₃ ≥ 0.

Общая сумма прибыли (целевая функция)

F = 1200х₁ + 1400х₂ + 1000х₃ = max.

Для решения задачи симплексным методом неравенства преобра­зуются в эквивалентные равенства путем добавления в каждое нера­венство по одному дополнительному неизвестному с коэффициентом + 1 и нулевым уравнением прибыли. Для удобства расчетов левые и правые части уравнений меняются местами. В этом случае исходные неравенства примут вид симплексных уравнений:

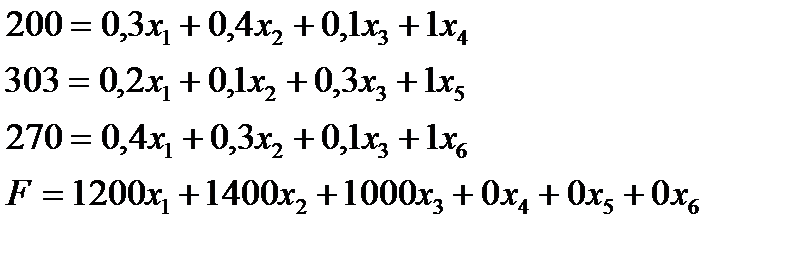
Коэффициенты при неизвестных записываются в симплексной таблице, в которой выполняются расчеты и отражаются полученные результаты.

В столбцах таблицы записывают: в первом (С_j) - прибыль единицы продукции, которая вводится в план выпуска; во втором (p₀) – неизвестные, включаемые в план; в третьем (х₀) – свободные величины; в остальных - коэффициенты при неизвестных уравнениях. В верхней части этих столбцов отражаются коэффициенты при неизвестных целевой функции.

Исходная таблица

сj	p0	x0
x1	x2	x3	x4	x5	x6
	x4		0,3	0,4	0,1
	x5		0,2	0,1	0,3
	x6		0,4	0,3	0,1
Zj - Cj		-1200	-1400	-1000

В нижней строке (целевой) записываются получаемые расчетным путем показатели: в столбце х₀ - суммарная прибыль планового выпуска, в остальных столбцах - прибыль единицы продукции с отрицательным знаком.

В последних трех столбцах коэффициенты при дополнительных неизвестных, равные единице, расположены по диагонали. Эта часть таблицы, называемая единичной подматрицей, необходима для вычислительных и аналитических целей.

При решении задач на максимум целевой функции наличие в целевой строке отрицательных чисел указывает на возможность начала или продолжения решения задачи. Порядок решения таков: из отрицательных чисел целевой строки выбирается наибольшее по модулю. Столбец, в котором оно находится, принимается за ключевой (или разрешающий) и для удобства расчетов выделяется. В нашем примере таким столбцом будет x₂, имеющий в целевой строке наибольшую по модулю величину - 1400.

Затем элементы столбца x₀ (свободные величины) делят на соответствующие коэффициенты ключевого столбца и полученные результаты сопоставляют между собой. Строка с наименьшим отно­шением принимается за ключевую и также для удобства выделяется. В нашем случае 200/0,4 = 500, 303/0,1= 3030, 270/0,3 = 900. Наимень­шее отношение 500 имеет строка х₄, она и будет ключевой. Ключевой элемент 0,4.

Далее элементы таблицы преобразуются и записываются в новую таблицу (1-я итерация). Первоначально преобразуют элементы ключевой строки путем деления их на ключевой элемент. Преобразованные элементы записывают в том же самом месте:

200/0,4 = 500; 0,3/0,4 = 0,75; 0,4/0,4 =1; 0,1/0,4 = 0,25; 1/0,4 = 2,5

В столбцах Р₀ и С_j занимают место вводимая в план неиз­вестная x₂ с прибылью 1400 (1-я итерация). Остальные элемен­ты преобразуются по следующему правилу:

- для преобразуемого элемента в его столбце находят элемент ключевой строки, а в его строке - элемент ключевого столбца;

- соответствующие элементы ключевой строки и ключевого столбца перемножаются и полученное произведение делят на ключевой момент;

- частное от деления вычитают из значения элемента, кото­рое он имел до преобразования, и полученный результат будет преобразованным элементом, который записывается в новую таблицу в том же самом месте.

Следуя этому правилу, преобразование элементов столбца х₀ будет:

303 -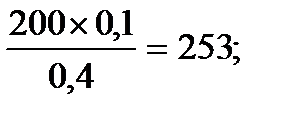

270 -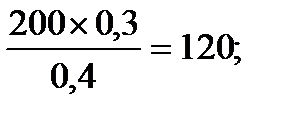

0 -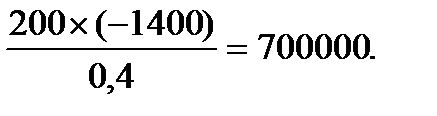

Остальные элементы таблицы вычисляются также по вышеизложенному правилу:

2-я строка – x₅ :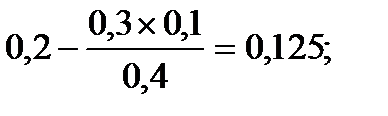

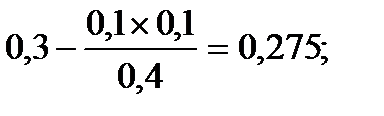
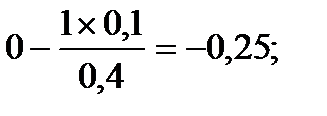
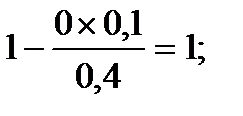
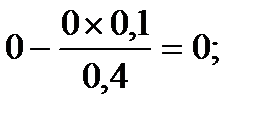
Включение на первой итерации в план неизвестной х₂ (выпуск продукции П₂ вида) обеспечит сумму прибыли 700000 руб.

1-я итерация

сj	p2	x0	x1	x2	x3	x4	x5	x6
	x2		0,75		0,25	2,5
	x5		0,125		0,275	-0,25
	x6		0,175		0,125	-0,75
Zj - Cj		-150		-650

Решение задачи продолжается, так как в целевой строке два отрицательных элемента. Наибольший по модулю элемент - 650. Он находится в столбце x₃, который принимается за ключевой, а ключевой строкой будет x₅

(500 : 0,25 =2000; 253 : 0,275 = 920; 120 : 0,125 = 960). Элементы таблицы преобразуются в том же порядке по изложенному правилу и записываются в новую таблицу (2-я итерация).

2-я итерация

сj	p2	x0	x1	x2	x3	x4	x5	x6
	x2		0,636			2,727	-0,91
	x3		0,455			-0,001	3,636
	x6		0,118			-0,636	-0,456
Zj - Cj		145,45			2909,1	2363,63

В последней таблице целевая строка имеет только положительные элементы. Это значит, что составленный план оптимален и дальнейшее улучшение его невозможно.

Как видно из таблицы, оптимальный план предусматривает выпуск продукции вида П₂ – 270 т (х₂ = 270), вида П₃ – 920 т (х₃ = 920), выпуск продукции вида П₁ производить не надо (х₁ = 0),. Дополнительные неизвестные (остатки сырья на складе) х₄ = 0, х₅ = 0, на складе осталось сырье третьего вида х₆= 5. Подставив значения неизвестных в уравнения, получим:

0,3*0 + 0,4*270 + 0,1*920 + 0 = 200

0,2*0 + 0,1*270 + 0,3*920 + 0 = 303

0,4*0 + 0,3*270 + 0,1*920 + 5 = 270

F = 1200*0 + 1400*270 + 1000*920 = 1298000

При постановке задачи были приняты ограничения только по запасам сырья (P₁, P₂, Р₃). Другие ограничения не учитывались. Но если бы в плане требовалось предусмотреть ассортиментные соотношения (например, выпуск продукции трех видов не должен превышать 1200 т, выпуск продукции вида П₂ должен быть не больше 400 т, а выпуск продукции вида П₃ должен быть не меньше 500 т, то в систему неравенств добавляются эти ограничения:

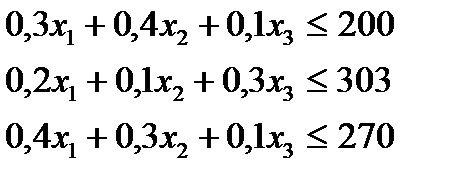
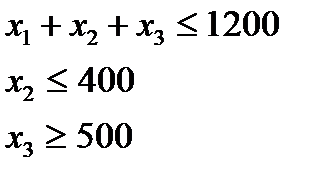
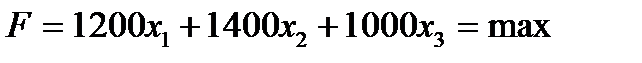
Эта система преобразуется в симплексные уравнения и решается по изложенным правилам.

Проведем анализ оптимального плана.

1) Запасы сырья первого и второго вида используются полностью без остатка, так как х₄ = х₅ = 0, на складе останется сырья третьего вида – 5 т (х₆ = 5).

2) Рассмотрим элементы матрицы.

Элементы столбца х₄ свидетельствуют: если запасы P₁ будут увеличены на I ед. (200 + 1), то выпуск продукции П₂ вида увели­чится на 2,727 ед. (х₂ = 270 + 2,727), выпуск продукции П₃ вида уменьшится на 0,001 ед. (920 – 0,001) на складе сырья третьего вида уменьшится на 0,636 т (х₆ = 5- 0,636). Сумма прибыли увеличится на 2909,1 руб.

Элементы столбца х₅ показывают, что увеличение запасов P₂ на I ед. (303 + 1) позволит увеличить выпуск продукции П₃ вида на 3,636 ед., уменьшится выпуск продукции П₂ вида на 0,91ед., прибыль увеличится на 2363,63 руб. Изменения объемов производства и суммы прибыли вызовет и уменьшение запасов Р₃ (х₆). Снижение запасов сырья приводит к изменениям выпуска продукции и суммы прибыли в обратном порядке.

Элементы целевой строки оптимального плана называются двойственными оценками, которые определяют величину изменения прибыли при изменении запасов сырья на I ед.

Многие экономико-математические методы реализованы в надстройке Excel Поиск решения, которую можно использовать для решения экономических задач. Можно рассмотреть решение ассортиментных задач с помощью надстройки Поиск решения.

Математическая модель должна содержать три основных компонента:

1. Переменные, значения которых необходимо вычислить (переменные из формальной модели).

2. Ограничения – записанные математически ограничения из формальной модели.

3. Целевая функция – это цель, записанная математически в виде функции от переменных. Обязательно указывается, что необходимо сделать с этой функцией для решения проблемы: найти ее максимум, минимум или конкретное заданное значение.

Перед выполнением каких-либо вычислений в Excel , надо перевести построенную математическую модель на рабочий лист Excel (рис.3).

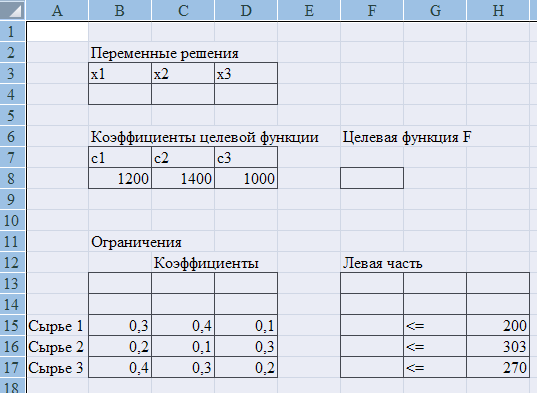
Рис. 3. Математическая модель в Excel

При создании табличной модели оптимизации в Excel следует учесть рекомендации, которые помогут применить средства Поиск решения:

1. Значения переменных располагаются в отдельных ячейках и группируются в отдельный блок ячеек.

2. Каждому ограничению отводится отдельная строка или столбец таблицы. Ограничения группируются в отдельный блок ячеек.

3. Желательно, чтобы ячейки, содержащие переменные и значение целевой функции, а также все ограничения, имели заголовки.

4. Коэффициенты целевой функции должны храниться в отдельной строке, располагаясь непосредственно под или над соответствующими переменными; формула для вычисления целевой функции должна находиться в соседней ячейке.

5. В каждой строке ограничений за ячейками, содержащими коэффициенты данного ограничения, следует ячейка, в которую записывается вычисленное значение функции ограничения (значение левой части ограничения). Желательно, чтобы правые части ограничений были константами, а не формулами.

Условия неотрицательности переменных решения необязательно включать в табличную модель. Можно непосредственно указать в диалоговом окне надстройки Поиск решения.

В табличной модели на рис. 3 значения переменных решения записаны в ячейках В4, С4 и D4.

Коэффициенты, стоящие перед переменными в формуле целевой функции, записаны в ячейки В8, С8 и D8, а само значение целевой функции F вычисляется в ячейке F8 (соответствующие заголовки записаны над этими ячейками). Ниже в диапазоне В15:D17 записаны коэффициенты функций ограничений, в диапазоне F15: F17 вычисляются значения левых частей ограничений, в диапазоне G15: G17 записаны знаки неравенств ограничений, в диапазоне H15: H17 значения правых частей ограничений.

Формулы, по которым выполняются все вычисления на рабочем листе, показаны на рис.4. для вычисления линейных функций подходит функция СУММПРОИЗВ (массив1;массив2), которая суммирует попарные произведения элементов двух диапазонов, заданных аргументами функции массив1имассив2.

Например, формула =СУММПРОИЗВ ($B$4:$D$4;B8:D8), вычисляющая значение целевой функции в ячейке F8, эквивалентна формуле: =B4*B8+C4*C8+D4*D8. Левые части ограничений, так как это линейные функции, также вычисляются с помощью функции СУММПРОИЗВ. Знаки неравенств в диапазоне G15: G17 вставлены только для пояснения ограничений.

После создания табличной модели можно использовать надстройку Excel Поиск решения, выбрав команду Поиск решения в меню. В открывшемся диалоговом окне Поиск решения надо указать данные, необходимые для поиска оптимального решения.

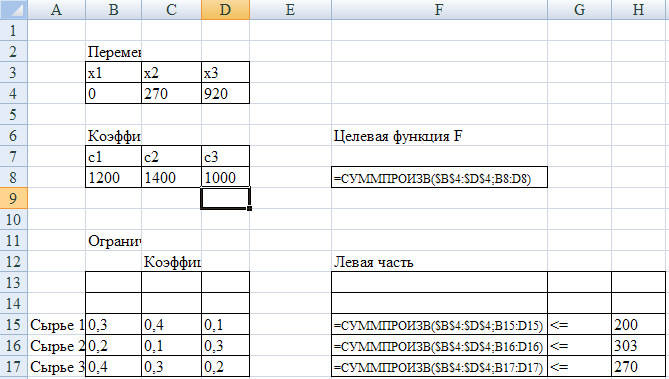
Рис. 4. Формулы табличной модели

В поле Установить целевую ячейкувводится адрес ячейки, содержащей значение целевой функции F8(рис. 5).

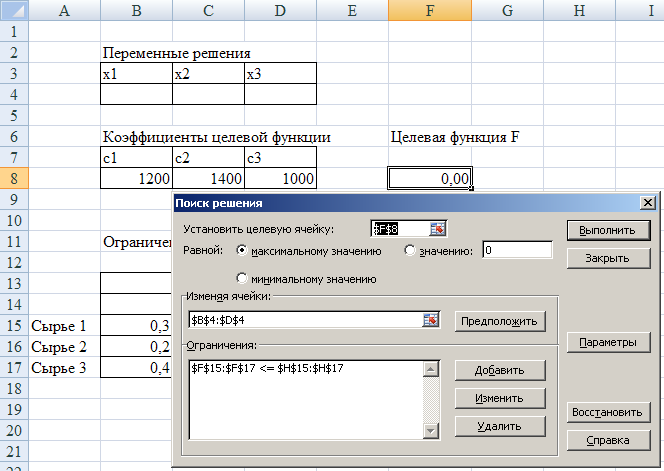
Рис. 5. Задание параметров для поиска решения

После этого надо добавить ограничения, нажимаем на кнопку Добавить, в поле Ссылка на ячейкувводим ссылку на диапазон F15: F17, в соседнем поле оставляем знак <= , а в поле Ограничениеуказываем на рабочем листе ссылку на диапазон H15: H17.

После задания ограничений надо нажать на кнопку Параметрыдиалогового окна Поиск решения. Откроется диалоговое окно (рис.6), в котором устанавливаются параметры.

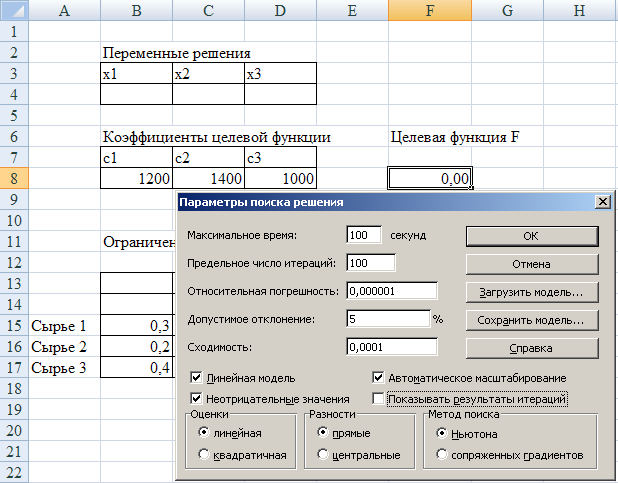
Рис. 6. Диалоговое окно Параметры поиска решения

В данном примере рассматривается линейная модель, поэтому надо установить флажок Линейная модель. В данной модели условия неотрицательности налагаются на все переменные, поэтому надо установить флажок Неотрицательные значения.

После задания необходимых данных надо щелкнуть на кнопке Выполнить.

После окончания работы Поиск решения выведет на экран диалоговое окно Результаты поиска решения (рис. 7), в котором можно указать, обновить ли исходную модель и создавать ли отчет.

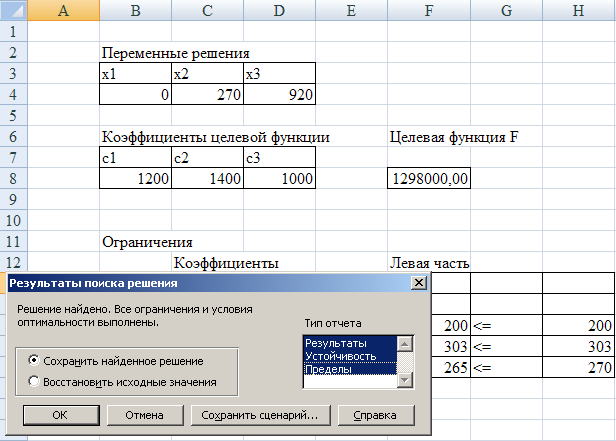
Рис. 7. Результаты поиска решения в Excel

Диалоговое окно Результаты поиска решения сообщает о завершении поиска. В данном примере в окне отобразилось сообщение Решение найдено. В диалоговом окне Результаты поиска решения также указали, что надо создать отчеты. Эти отчеты используются для дальнейшего анализа альтернативных вариантов решения.