Виды, источники и носители информации, защищаемой техническими средствами. Демаскирующие признаки объектов защиты информации и их классификация
Виды И:
| Семантическая | Нац.языки |
| Проф.языки | |
| Признаковая | Видовая(форма,цвет,размер) |
| Вещественная(из чего состоит) | |
| Сигнальная |
Носители И - мат.объекты в кот. И находят отображение в виде символов, образов, сигналов и тех.решений:
· люди
· мат.тела
· поля
· элементарные частицы
Демаскирующие признаки:
· прямые = опознавательные (например ТЭЦ имеет длинную трубу)
· косвенные = признаки деятельности(например тень от трубы ТЭЦ)
| По характеристикам | По информативности | По времени проявления |
| · видовые · сигнальные · вещественные | · именные · косвенные · прямые | · постоянные · периодические · эпизодические |
Схема блока, характеризующего направление религии и возможные угрозы при прогнозировании стабильности государства.
| Моно религия | Несколько |
| · Мировая(православие, католицизм, протестантизм, ислам, буддизм) · Национальная(индуизм, конфуцианство, синтоизм, иудаизм) · Культура |
В зависимости от % соотношения представителей каждой религии возможны конфликты на религиозной почве
Написать формулу расчета коэффициента по форме правления, административно-территориальному устройству и весу фактора государственного строя при прогнозировании стабильности государства.
< Билет 9 >
1. Определение и нормативное закрепление состава защищаемой информации. Определение объектов защиты.
2. Схема блока, характеризующего экономику государства и возможные угрозы при прогнозировании стабильности государства.
3. Трендовые модели на основе кривых роста
Вопрос 1 а)Определение и нормативное закрепление состава защищаемой информации. б) Определение объектов защиты.
Ответ:
А) Создавая систему информационной безопасности, необходимо четко понимать, что без правового обеспечения защиты информации любые последующие претензии с стороны организации к недобросовестному сотруднику, клиенту, конкуренту и должностному лицу окажутся беспочвенными. Если перечень сведений конфиденциального характера не доведен своевременно до каждого сотрудника (при условии, что он допущен по должностным обязанностям) в письменном виде, то сотрудника, укравшего важную информацию, невозможно будет привлечь к ответственности.
Таким образом, состав защищаемой информации в каждой организации должен быть четко определен и задокументирован.
Для определения состава защищаемой информации необходимо ответить на вопросы:
1) Какие сведения следует охранять? 2) Кого они интересуют?
3) Почему они нуждаются в получении этих сведений?
4) Какие виды информации имеются в данной организации?
5) Какова ценность каждого из видов информации
6) Какая защита необходима для каждого вида информации?
Кроме того, государственные законодательные акты оговаривают следующие виды защищаемой информации:
1) Информация, относящаяся к государственной тайне – ФЗ "О ГТ ", Указ Президента РФ «О перечне сведений, составляющих ГТ»
2) Информация, составляющая коммерческую тайну. Постановление правительства РФ «О перечне сведений, которые не могут составлять коммерческую тайну», Гражданский кодекс РФ, Закон «О коммерческой тайне».
3) Информация, составляющая банковскую тайну. Закон «О банках и банковской деятельности».
4) Информация, составляющая профессиональную тайну. Указ Президента РФ «Об утверждении перечня сведений конфиденциального характера».
Правовые нормы обеспечения безопасности и защиты информации на конкретном предприятии (фирме, организации) отражаются в совокупности учредительных, организационных и функциональных документов.
Требования обеспечения безопасности и защиты информации отражаются в Уставе (учредительном договоре) в виде следующих положений:
– предприятие имеет право определять состав, объем и порядок защиты сведений конфиденциального характера, требовать от своих сотрудников обеспечения их сохранности и защиты от внутренних и внешних угроз;
– предприятие обязано обеспечить сохранность конфиденциальной информации.
Опираясь на государственные правовые акты и учитывая ведомственные интересы на уровне конкретного предприятия (фирмы, организации), разрабатываются собственные нормативно-правовые документы, ориентированные на обеспечение информационной безопасности. К таким документам относятся:
– Положение о сохранении конфиденциальной информации;
– Перечень сведений, составляющих конфиденциальную информацию;
– Инструкция о порядке допуска сотрудников к сведениям, составляющим конфиденциальную информацию;
– Положение о специальном делопроизводстве и документообороте;
– Перечень сведений, разрешенных к опубликованию в открытой печати;
– Положение о работе с иностранными фирмами и их представителями;
– Обязательство сотрудника о сохранении конфиденциальной информации;
– Памятка сотруднику о сохранении коммерческой тайны.
Обязательства конкретного сотрудника, рабочего или служащего в части защиты информации обязательно должны быть оговорены в трудовом договоре (контракте). Трудовой договор – это правовая основа к тому, чтобы пресечь неверные или противоправные действия работника.
Б)Собственно информация является предметом защиты в системах безопасности, а объектами защиты являются носители информации. Поскольку носители информации имеют разную физическую природу и информация в своем движении даже в одном технологическом процессе часто переходит из одной формы в другую, определить полный перечень объектов, подлежащих защите – задача не простая.
Обычно объекты защиты определяют по основному признаку – содержат ли они или циркулирует ли в них информация ограниченного доступа. Определение объектов защиты при построении комплексной системы защиты информации. Классификация объектов информационной защиты может быть представлена в виде такой схемы:
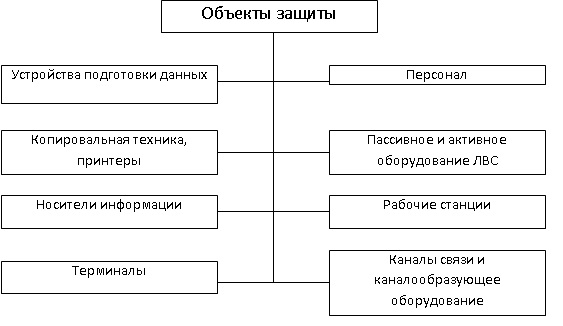
Вопрос 2Схема блока, характеризующего экономику государства и возможные угрозы при прогнозировании стабильности государства.
Ответ:
 | |||
 |
Моноразвитые экономики(экономика построенная на одной кокой-то отросли)
Зависимость от экспорта и импорта
ВВП - совокупная стоимость всех благ производимых на территории данной страны за год в денежном эквиваленте.
ВНП -это ВВП за вычетом прибыли иностранных компаний, но с добавлением прибыли полученной гражданами страны за её пределами
ВНП и ВВП считаются по налогообложениям.
ВНП на душу населения свидетельствует об уровне развития страны
Вопрос 3Трендовые модели на основе кривых роста.
Ответ:
Изучение основной тенденции развития на основе методов механического выравнивания является эмпирическим приемом предварительного анализа. Для того чтобы дать количественную оценку изменений динамического ряда, используется метод аналитического выравнивания. В этом случае фактические уровни ряда заменяются теоретическими, рассчитанными по определенной кривой, отражающей общую тенденцию изменения показателя во времени.
Для этого используются трендовые эконометрические модели с одним параметром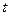 
, представляющим моменты наблюдения (время). Эти модели получили название кривых роста. Оценка параметров кривых роста и проверка их качества проводится так же как и для регрессионных однофакторных моделей. Для целей краткосрочного и среднесрочного прогнозирования эти модели они являются надежным инструментом.
В настоящее время насчитывается большое количество типов кривых роста для экономических процессов. Чтобы правильно подобрать наилучшую кривую роста для моделирования и прогнозирования экономического явления, необходимо знать особенности каждого вида кривых. Наиболее часто в экономике используются полиномиальные, экспоненциальные и S-образные кривые роста.
1. При равномерном развитии — линейная функция: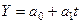 
(полином первой степени)
2. При росте с ускорением:
а) полином второй степени (парабола второго порядка):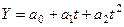 
б) полином третьей степени (кубическая парабола):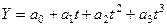 
3. При постоянных темпах роста — показательная функция: Yt = b0b1t;
4. При снижении с замедлением — гиперболическая функция:
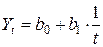
5. Для процессов, имеющих асимптотическое развитие используют S–образные кривые(модифицированную экспоненту, логистическую кривую, кривую Гомперца). Используют и другие функции.
Для сглаживания экономических временных рядов нецелесообразно использовать функции, содержащие большое количество параметров, так как полученные таким образом уравнения тренда (особенно при малом числе наблюдений) будут отражать случайные колебания, а не основную тенденцию развития явления.
Выбор того или иного уравнения кривой роста основан на свойствах этих кривых. Рассмотрим полиномиальные кривые: параметр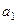 
называют линейным приростом, параметр 
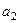– ускорением роста, параметр 
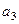– изменением yскорения роста.
Для полинома первой степени характерен постоянный закон роста. Если рассчитать первые приросты по формуле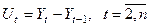 
то они будут постоянной величиной, равной .
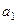Если первые приросты рассчитать для полинома второй степени, то они будут иметь линейную зависимость от времени и ряд из первых приростов Ut— на графике будет представлен прямой линией. Вторые приросты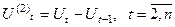 
для полинома второй степени будут постоянны.
Для полинома третьей степени первые приросты будут полиномами второй степени, вторые приросты будут линейной функцией времени, а третьи приросты, рассчитываемые по формуле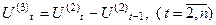 
, будут постоянной величиной.
Полиномиальные кривые роста можно использовать для аппроксимации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня.
В отличие от использования полиномиальных кривых использование экспоненциальных кривых роста предполагает, что дальнейшее развитие зависит от достигнутого уровня, например, прирост зависит от значения функции. В экономике чаще всего применяются две разновидности экспоненциальных (показательных) кривых: простая экспонента и модифицированная экспонента.
Простая экспонента представляется в виде функции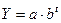 
где а и b– положительные числа, при этом если b больше единицы, то функция возрастает с ростом времени t, если b меньше единицы – функция убывает.
Можно заметить, что ордината данной функции изменяется с постоянным темпом прироста. Если взять отношение прироста к самой ординате, оно будет постоянной величиной:
.
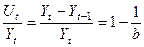Прологарифмируем выражение для данной функции по любому основанию: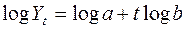 
. Отсюда можно заметить, что логарифмы ординат простой экспоненты линейно зависят от времени.
Модифицированная экспонента имеет вид: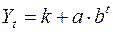 
,
где постоянные величины: а меньше нуля, b положительна и меньше единицы, а константа k носит название асимптоты этой функции, т.е. значения функции неограниченно приближаются (снизу) к величине k. Могут быть другие варианты модифицированной экспоненты, но на практике наиболее часто встречается указанная выше функция.
Если прологарифмировать первые приросты данной функции, 
то получится функция, линейно зависящая от времени, а если взять отношение двух последовательных приростов, то оно будет постоянной величиной:
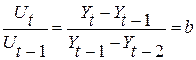
В экономике достаточно распространены процессы, которые сначала растут медленно, затем ускоряются, а затем снова замедляют свой рост, стремясь к какому-либо пределу. В качестве примера можно привести процесс ввода некоторого объекта в промышленную эксплуатацию, процесс изменения спроса на товары, обладающие способностью достигать некоторого уровня насыщения, и др. Для моделирования таких процессов используются так называемые S-образные кривые роста, среди которых выделяют кривую Гомперца и логистическую кривую.
Кривая Гомперца имеет следующее уравнение: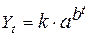 
,
Где а, b — положительные параметры, причем b меньше единицы; параметр k – асимптота функции.
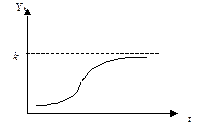
В кривой Гомперца выделяются четыре участка: на первом– прирост функции незначителен, на втором –прирост увеличивается, на третьем участке прирост примерно постоянен, на четвертом – происходит замедление темпов прироста и функция неограниченно приближается к прямой Y=k. В результате конфигурация кривой напоминает латинскую букву S.
Логарифм данной функции является экспоненциальной кривой; логарифм отношения первого прироста к самой ординате функции — линейная функция времени.
На основании кривой Гомперца описывается, например, динамика показателей уровня жизни; модификации этой |кривой используются в демографии для моделирования показателей смертности и т. д.|
Логистическая кривая, или кривая Перла–Рида является возрастающей функцией, наиболее часто выражаемой в виде: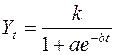 
Другие виды этой кривой: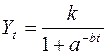 
; 
.
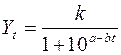В этих выражениях а и b – положительные параметры; k – предельное значение функции при бесконечном возрастании времени.
Если взять производную данной функции, то можно увидеть, что скорость возрастания логистической кривой в каждый момент времени пропорциональна достигнутому уровню функции и разности между предельным значением k и достигнутым уровнем. Логарифм отношения первого прироста функции к квадрату ее значения (ординаты) есть линейная функция от времени.
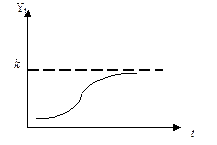
Конфигурация графика логистической кривой близка графику кривой Гомперца, но в отличие от последней, логистическая кривая имеет точку симметрии, совпадающую с точкой перегиба.
< Билет 10 >