Перевод целых чисел из десятичной системы счисления в систему счисления с другим основанием

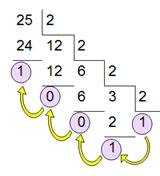Рис. 16. Перевод числа из десятичной СС в двоичную.

Для осуществления такого перевода необходимо делить число с остатком на основание системы счисления до тех пор, пока частное больше основания системы счисления.

Пример перевода десятичного числа 25₍₁₀₎ в двоичный вид показан на рисунке 16.

Результат перевода записывается в обратном порядке, т.е. начиная с последнего результата деления.

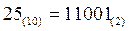
Шестнадцатеричная система счисления

Система счисления с основанием 16 интересна тем, что она включает в себя больше разрядов, чем десятичная, и соответственно десяти арабских цифр недостаточно для алфавита этой системы счисления, поэтому в качестве недостающих цифр в ней используются буквы латинского алфавита.

Для обозначения того, что запись является шестнадцатеричным числом, принято использовать также символ #.

Таблица 7.

Основание СС (k)	Цифры, составляющие алфавит СС	Пример записи
	0, 1	&101011111
	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f 10 11 12 13 14 15	#15f

Для шестнадцатеричной системы счисления действуют те же правила перевода, что и для всякой позиционной системы счисления.

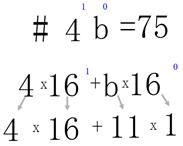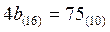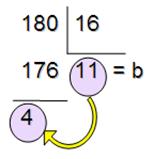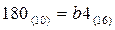Рис. 17а. Перевод из СС с основанием 10 в СС с основанием 16.	Рис. 17b. Перевод из СС с основанием 16 в СС с основанием 10.

Вавилонская (шестидесятеричная) система счисления

Исторический интерес представляет так называемая «вавилонская», или шестидесятеричная система счисления, весьма сложная, существовавшая в Древнем Вавилоне, за две тысячи лет до н.э.

Это первая известная нам система счисления, основанная на позиционном принципе. Система вавилонян сыграла большую роль в развитии математики и астрономии, ее следы сохранились до наших дней. Так, мы до сих пор делим час на 60 минут, а минуту на 60 секунд. Точно так же, следуя примеру вавилонян, окружность мы делим на 360 частей (градусов).

Задачи

1. Числа в двоичной системе счисления имеют вид 11₍₂₎ и 101₍₂₎ . Чему равно их произведение в десятичном виде? Варианты: 60, 15, 1111, 8.

2. Чему равна разность 25 - &1101. Варианты: &1100, 13.

3. В десятичной - 8;

- в двоичной - [ ];

- в восьмеричной - [ ];

- в шестнадцатеричной - [ ].

4. Количество чисел, которое можно закодировать нулями и единицами в 10 позициях, равно: 128, 256, 1024, 2048?

5. Укажите истинное высказывание:

- #a < &1100;

- #a > &1100;

- #a = &1100.

6. Дано равенство 23_(k)+33_(k)=122_(k). Чему равно k? Варианты: 2, 3, 4, 10.

7. Какое число предшествует шестнадцатеричному числу #6afa? Варианты: #6afb, #6a10, #6af9, #5afa.

8. Шестнадцатеричное число #4d в десятичной системе счисления это: 43, 77, 177, 176?

9. Прочитайте стихотворение. Переведите встречающиеся в нем числительные из двоичной системы счисления в десятичную.

Необыкновенная девчонка
А. Н. Стариков

Ей было тысяча сто лет,
Она в 101-ый класс ходила,
В портфеле по сто книг носила –
Все это правда, а не бред.

Когда, пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.

Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали.

И десять темно-синих глаз
Рассматривали мир привычно,…
Но станет все совсем обычным,
Когда поймете наш рассказ.

10. За праздничным столом собрались 4 поколения одной семьи: дед, отец, сын и внук. Их возраст в различных системах счисления записывается так 88 лет, 66 лет, 44 года и 11 лет. Сколько им лет в десятичной системе счисления, если через год их возраст в тех системах счисления можно будет записать как 100?