Алгоритм построения сетевой модели

Общие сведения

Сетевая модель (сетевой график, сеть) – это математическая модель, отражающая комплекс работ и событий, отображающих процесс достижения определенной цели и связанных с реализацией некоторого проекта, их технологической и логической последовательностью и связями. Сетевая модель (СМ) может быть представлена в виде графика или таблицы.

Анализ сетевой модели – это выявление взаимосвязи этапов реализации проекта и определение наиболее оптимального порядка выполнения этих этапов с целью сокращения сроков выполнения.

Основные понятия СМ: событие, работа и путь. На рисунке 7.1 представлена СМ, состоящая из 11 событий (кружки на рисунке) и 16 работ (стрелки), продолжительность выполнения которых указана над стрелками.

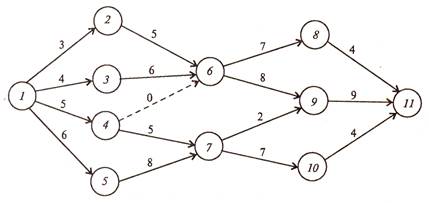
Рисунок 7.1 – Сетевая модель

Работа характеризует материальное действие, требующее использования ресурсов, или логическое действие, требующее лишь взаимосвязи событий. Работа обозначается парой упорядоченных чисел (i, j), где i – номер события, из которого выходит стрелка, обозначающая работу, j – номер события, в которое она входит. Работа не может начаться раньше, чем совершится событие, которое ей предшествует. Каждая работа имеет определенную продолжительность t(i, j). Например, запись t(2, 6) = 5 означает, что работа (2, 6) имеет продолжительность 5 единиц. К работам относятся также процессы, не требующие ни ресурсов, ни времени выполнения. Они заключаются в установлении логической взаимосвязи работ и показывают, что одна из них непосредственно зависит от другой; такие работы называются фиктивными, на графике изображаются пунктирными стрелками (рисунок 7.1, работа (4, 6)).

Событие – это результат выполнения одной или нескольких работ. Оно не имеет протяженности во времени, так как совершается в тот момент, когда оканчивается последняя входящая в него работа. События имеют порядковый номер i (i = 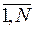). В СМ имеется начальное событие (1), не имеющее предшествующих работ и событий, из которого работы только выходят, и конечное (N), в которое работы только входят, не имеющее последующих работ и событий.

Путь – это цепочка следующих друг за другом работ, соединяющих начальную и конечную вершины. На рисунке 7.1 путями являются L₁ = (1, 2, 6, 9, 11), L₂ = (1, 4, 7, 9, 11), L₃ = (1, 4, 6, 8, 11) и др. Продолжительность пути – это сумма продолжительностей составляющих его работ. Путь, имеющий максимальную длину, называют критическим (L_кр), его продолжительность – t_кр. Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ.

Сетевые модели имеют ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов. Но перед расчетом СМ следует убедиться, что она удовлетворяет следующим основным требованиям:

1. События правильно пронумерованы, то есть для каждой работы (i, j) i < j. При невыполнении этого требования необходимо использовать алгоритм перенумерации событий, который заключается в следующем:

- нумерация событий начинается с исходного события, которому присваивается номер 1;

- из исходного события вычеркивают все исходящие из него работы, на оставшейся сети находят событие, в которое не входит ни одна работа, ему присваивают номер 2;

- затем вычеркивают работы, выходящие из события номер 2, вновь находят событие, в которое не входит ни одна работа, ему присваивают номер 3, так продолжается до завершающего события, номер которого должен быть равен количеству событий в сетевом графике;

- если при очередном вычеркивании работ одновременно несколько событий не имеют входящих в них работ, то их нумеруют очередными номерами в произвольном порядке.

2. Отсутствуют тупиковые события (кроме завершающего), за которыми не следует хотя бы одна работа.

3. Отсутствуют события (за исключением исходного), которым не предшествует хотя бы одна работа.

4. Отсутствуют циклы, то есть замкнутые пути, соединяющие событие с ним же самим.

Для событий рассчитывают три характеристики: ранний и поздний срок совершения события, а также его резерв.

Ранний срок совершения события – это величина наиболее длительного отрезка пути от исходного до рассматриваемого события, причем t_p(1) = 0, а t_p(N) = t_кр(L):

t_p(j) = 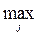{t_p(i) + t(i, j)}, j = 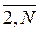. (7.1)

Поздний срок совершения события характеризует самый поздний допустимый срок, к которому должно совершиться событие, не вызывая при этом срыва срока совершения конечного события:

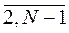t_п(i) = {t_п(j) + t(i, j)}, i = . (7.2)

Этот показатель определяется «обратным ходом», начиная с завершающего события, с учетом соотношения t_п(N) = t_p(N).

Все события, за исключением событий, принадлежащих критическому пути, имеют резерв R(i), который показывает, на какой предельно допустимый срок можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения всего комплекса работ:

R(i) = t_п(i) – t_p(i). (7.3)

Для всех работ (i, j) на основе ранних и поздних сроков совершения всех событий можно определить показатели (таблица 7.1).

Таблица 7.1

Показатели сетевой модели

Показатели работы	Формула
Ранний срок начала	tрн(i, j) = tр(i)
Ранний срок окончания	tро(i, j) = tр(i) + t(i, j)
Поздний срок начала	tпо(i, j) = tп(j)
Поздний срок окончания	tпн(i, j) = tп(j) – t(i, j)
Полный резерв времени	Rп(i, j) = tп(j) – tp(i) – t(i, j)
Частный резерв времени первого вида	Rl(i, j) = tп(j) – tп(i) – t(i, j) или Rl(i, j) = Rп(i, j) – R(i)
Частный резерв времени второго вида (свободный)	Rc(i, j) = tp(j) – tp(i) – t(i, j) или Rc(i, j) = Rп(i, j) – R(j)
Независимый резерв	Rн(i, j) = max {0; tp(j) – tп(i) – t(i, j)} = max{0; Rп(i, j) – R(i) – R(j)}

Полный резерв времени показывает, на сколько можно увеличить время выполнения конкретной работы при условии, что срок выполнения всего комплекса работ не изменится.

Частный резерв времени первого вида – часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события.

Частный резерв времени второго вида (свободный резерв) – часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события.

Независимый резерв времени соответствует случаю, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки. Использование этого резерва не влияет на величину резервов времени других работ.

Графическая интерпретация характеристик СМ представлена на рисунке 7.2.

Путь характеризуется двумя показателями: продолжительностью и резервом. Продолжительность пути – это сумма продолжительностей составляющих его работ. Резерв – это разность между длинами критического и рассматриваемого путей. Работы, лежащие на критическом пути, сам критический путь имеют нулевой резерв времени. Резерв времени пути показывает, на сколько может увеличиться продолжительность работ данного пути, без изменения продолжительности общего срока выполнения всех работ.

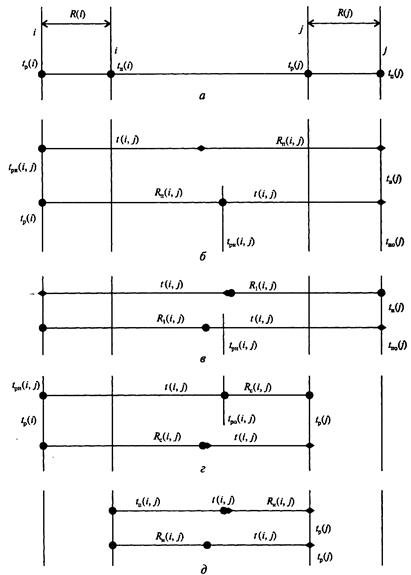
Рисунок 7.2 – Характеристики сетевой модели

Для оптимизации сетевой модели, выражающейся в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения, необходимо оценить степень трудности своевременного выполнения всех работ, а также «цепочек» пути. Более точной оценкой по сравнению с полным резервом является коэффициент напряженности:

K_н(i, j) = 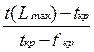= 1 – 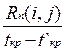. (7.4)

где t(L_max) – продолжительность максимального пути, проходящего через работу (i, j);

t'_кр – продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем.

Коэффициент напряженности изменяется от 0 до 1. Чем он ближе к 1, тем сложнее выполнить данную работу в установленный срок. Самыми напряженными являются работы критического пути, для которых он равен 1. На основе коэффициента напряженности все работы СМ делятся на три группы:

- напряженные (K_н(i, j) > 0,8);

- подкритические (0,6 < K_н(i, j) ≤ 0,8);

- резервные (K_н(i, j) ≤ 0,6).

В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ, что возможно при переводе всех работ в первую группу. При расчете этих показателей целесообразно пользоваться графиком СМ.

Перечисленные выше характеристики СМ могут быть получены на основе приведенных аналитических формул, а процесс вычислений отображен непосредственно на графике или представлен матрицей размерности nхn, или таблицей.

Алгоритм построения сетевой модели

1. Весь процесс разбивается на работы.

2. Составляется перечень работ и событий.

3. Продумывается логическая связь между работами и событиями и последовательность их выполнения.

4. Работы закрепляются за конкретными исполнителями.

5. Оценивается длительность работ.

6. Составляется сетевой график («сшивается» график).

7. Рассчитываются параметры событий и работ, определяются резервы времени и критический путь.

8. Проводится анализ и оптимизация графика, в результате которого может быть перестроен сетевой график.

Пример 7.1. Провести анализ сетевой модели, представленной на рисунке 7.3. Перечень работ и их продолжительность укажем во второй и третьей графах таблицы 7.2, последовательно записывая во второй графе работы, начинающиеся с номера 1, затем с номера 2 и т. д.

В первой графе поставим количество работ К_пр, непосредственно предшествующих событию, с которого начинается рассматриваемая работа. Для работ, начинающихся с номера 1, предшествующих работ нет. Для k-й работы просматриваются все верхние строки второй графы таблицы и отыскиваются строки, оканчивающиеся на этот номер. Количество найденных работ записывается в строки, начинающиеся с номера k. Например, для работы (5, 8) в первой графе поставим цифру 3, так как во второй графе на номер 5 оканчиваются три работы: (2, 5), (3, 5) и (4, 5).

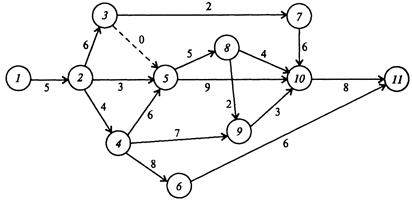
Рисунок 7.3 – Сетевая модель

Заполнение таблицы начинается с расчета раннего срока начала работ. Для работ, имеющих число ноль в первой графе, в 4-ю графу заносятся нули, а их значение в 5-й графе получается в результате суммирования чисел 3-й и 4-й граф. В рассматриваемом примере таких работ только одна – (1, 2), поэтому в 4-й графе в соответствующей ей строке проставим 0, а в 5-й графе 0 + 5 = 5.

Для заполнения следующих строк 4-й графы, то есть строк, начинающихся с номера 2, просматриваются заполненные строки 5-й графы, содержащие работы, которые оканчиваются на этот номер, максимальное значение переносится в 4-ю графу «обрабатываемых» строк. В данном случае такая работа лишь одна (1, 2), о чем можно судить по 1-й графе. Число 6 из 5-й графы переносим в 4-ю графу для всех работ, начинающихся с номера 2, то есть в три последующие строки с номерами (2, 3), (2, 4), (2, 5). Далее для каждой из этих работ путем суммирования значений 3-й и 4-й граф сформируем значение 5-й графы:

t_ро(2, 3) = 6+5 =11, t_ро(2, 4) = 4+5 =9, t_ро(2, 5) = 3+5 =8.

Этот процесс повторяется до тех пор, пока не будет заполнена последняя строка таблицы 7.2.

Шестая и седьмая графы заполняются «обратным ходом», то есть снизу вверх. Для этого просматриваются строки, оканчивающиеся на номер последнего события, и из 5-й графы выбирается максимальная величина, которая записывается в 7-ю графу по всем строкам, оканчивающимся на номер последнего события (см. формулу t_п(N) = t_p(N)). В нашем случае t(N) = 33. Затем для этих строк находится содержимое 6-й графы как разность значений 7-й и 3-й граф. Имеем: t_ро(10, 11) = 33 – 8 = 25. Далее просматриваются строки, оканчивающиеся на номер события, которое непосредственно предшествует завершающему событию (10). Для определения значений 7-й графы этих строк (работы (5, 10), (7, 10), (8, 10), (9, 10)) просматриваются все строки 6-й графы, лежащие ниже и начинающиеся с номера 10.

Таблица 7.2

Расчет основных показателей сетевой модели

Кпр	(i, j)	t(i, j)	tрн(i, j)=tр(i)	tро(i, j)	tпн(i, j)	tпо(i, j)=tп(j)	Rп	Kн
				5=4+3	6=7–3
	(1, 2)
	(2, 3)							0,8
	(2, 4)
	(2, 5)							0,65
	(3, 5)							0,8
	(3, 7)							0,7
	(4, 5)
	(4, 6)							0,58
	(4, 9)							0,54
	(5, 8)
	(5, 10)							0,95
	(6, 11)							0,58
	(7, 10)							0,7
	(8, 9)
	(8, 10)							0,93
	(9, 10)
	(10, 11)

В 6-й графе среди них выбирается минимальная величина, которая переносится в 7-ю графу по обрабатываемым строкам. В нашем случае она одна – (10, 11), поэтому заносим во все строки указанных работ число 25. Процесс повторяется до тех пор, пока не будут заполнены все строки 6-й и 7-й граф.

Содержимое 8-й графы равно разности значений 6-й и 4-й граф или 7-й и 5-й граф (см. формулы в таблице 7.1).

Учитывая, что нулевой резерв времени имеют только события и работы, принадлежащие критическому пути, получаем, что критическим является путь L_кр = (1, 2, 4, 5, 8, 9, 10, 11), t_кр = 33 дня.

Рассчитаем коэффициент напряженности. Для работ критического пути (1, 2), (2, 4), (4, 5), (5, 8), (8, 9), (9, 10), (10, 11) К_н = 1.

Для других работ:

K_н = (2, 3) = 1 – 4/ (33 – (5+8)) = 1 – 0,2 = 0,8;

K_н = (4, 9) = 1 – 6/ (33 – (5+4+3+8)) = 1 – 0,46 = 0,54;

K_н = (5, 10) = 1 – 1/ (33 – (6+3+6+9)) = 1 – 0,05 = 0,95 и т. д.

В соответствии с полученными значениями K_н можно утверждать, что оптимизация сетевой модели возможна за счет резервов работ (4, 6), (4, 9) и (6, 11).