Перевод чисел из одной системы счисления в другую

Представление чисел в развернутой форме одновременно является способом перевода чисел в десятичную систему из любой другой позиционной системы счисления. Достаточно подсчитать результат по правилам десятичной арифметики.

Например, надо получить десятичные эквиваленты чисел: 101,01₂; 673,2₈; 15AC₁₆.

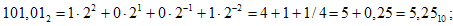
Перевод десятичного числа в другую систему счисления может выполняться разными способами. При этом надо учитывать, что алгоритмы перевода целых чисел и правильных дробей будут отличаться. Для смешанного числа целая и дробная части переводятся отдельно по соответствующим алгоритмам. В итоговой записи искомого они объединяются и разделяются запятой.

Так называемый метод поэтапного деления заключается в последовательном целочисленном делении исходного числа и получаемых неполных частных на основание той системы счисления, в которую осуществляется перевод. Остатки от деления составляют искомое число.

Алгоритм перевода целого десятичного числа Nв позиционную систему с основанием p:

1. Разделить нацело число N на p.

2. Полученный остаток от деления дает цифру, стоящую в нулевом разряде p-ичной записи числа N.

3. Полученное частное снова разделить нацело на p и снова запомнить полученный остаток - это цифра первого разряда, и т.д.

4. Такое последовательное деление продолжается до тех пор, пока частное не станет равным 0.

5. Цифрами искомого числа являются остатки от деления, выписанные слева направо начиная с последнего полученного остатка.

Для оформления записи перевода предлагается один из возможных способов: слева от черты записываются неполные частные от целочисленного деления на основание, а справа - остатки от деления.

Например, надо перевести десятичное число 26 в двоичную, троичную и шестнадцатеричную системы счисления.

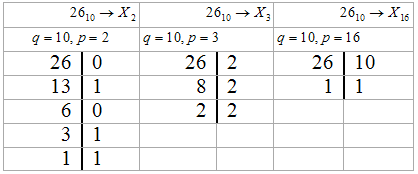
Результат: 26₁₀=11010₂, 26₁₀=222₃, 26=1A₁₆.

Алгоритм перевода правильной десятичной дроби Nв позиционную систему с основанием p:

1. Умножить данное число на новое основание p.

2. Целая часть полученного произведения является цифрой старшего разряда искомой дроби.

3. Дробная часть полученного произведения вновь умножается на p, и целая часть результата считается следующей цифрой искомой дроби.

4. Операции продолжать до тех пор, пока дробная часть не окажется равной нулю либо не будет достигнута требуемая точность.

Например, надо перевести десятичную дробь 0,375 в двоичную, троичную и шестнадцатеричную систему счисления. Перевод выполнить с точностью до третьего знака.

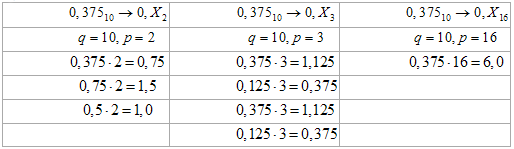
Результат: 0,375₁₀=0,011₂; 0,375₁₀=0,101₂; 0,375₁₀=0,6₁₆.

Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a₀*pⁿ + a₁*p^n-1 + ... + a_n-1*p¹ + a_n*p⁰, где a₀ ... a_n - это цифры данного числа в системе счисления с основанием p.

Например, переведем число 4A3F в десятичную систему. По определению, 4A3F= 4*16³+A*16²+3*16+F. Заменив A на 10, а F на 15, получим 4*16³+10*16²+3*16+15= 19007.

Пожалуй, проще всего осуществляется перевод чисел из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2ⁿ, нужно

· данное двоичное число разбить справа налево на группы по n-цифр в каждой;

· если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов;

· рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2ⁿ.

Двоично-шестнадцатеричная таблица

2-ная
16-ная
2-ная
16-ная			A	B	C	D	E	F

Двоично-восьмеричная таблица

2-ная
8-ная

Например, надо перевести в восьмеричную и шестнадцатеричную системы счисления число 1011000010,0011001₂.

Для этого разобьем исходное число на группы по 3 цифры, начиная от десятичной запятой, и заменим триады восьмеричными цифрами:

001 011 000 010 , 001 100 100	- 2-ичное число;
1 3 0 2 , 1 4 4	- 8-ричное число.

Разобьем число на группы по 4 цифры, начиная от десятичной запятой, и заменим тетрады шестнадцатеричными цифрами:

0010 1100 0010 , 0011 0010	- 2-ичное число;
2 С 2 , 3 2	- 16-ричное число.

Результат: 1011000010,0011001₂=1302,144₈=2C2,32₁₆