Перевод правильных дробей из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления
Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Пример.
Перевести 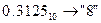 с.с.
с.с.
| 3125 ´ 8 | |
| 5000 ´ 8 | |
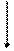
Результат 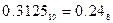 .
.
Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Пример.
Перевести 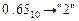 с.с. Точность 6 знаков.
с.с. Точность 6 знаков.
| 65´ 2 | ||
| 3 ´ 2 | ||
| 6 ´ 2 | ||
| 2 ´ 2 | ||
| 4 ´ 2 | ||
| 8 ´ 2 | ||
| 6 ´ 2 | ||
| . . . |
Результат 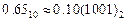 .
.
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Пример. Перевести 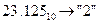 с.с.
с.с.
1) Переведем целую часть: 2) Переведем дробную часть:
 | ||||
 |
125  2 2 | |
25 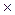 2 2 | |
5 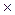 2 2 | |

Таким образом 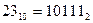 ;
; 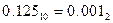 . Результат:
. Результат: 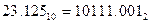 .
.
Необходимо отметить, что целые числа остаются целыми, а правильные дроби – дробями в любой системе счисления.
Для перевода восьмеричного или шестнадцатеричного числа в двоичную формудостаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.
Пример. а) 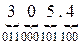 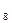 = = 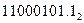 ; ; |
б) 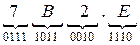
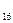 =
= 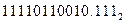 .
.
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системепоступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
Пример.
а) Перевести 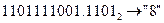 с.с.
с.с.
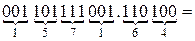
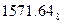
б) Перевести 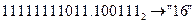 с.с.
с.с.
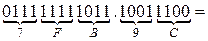
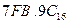
Перевод из восьмеричной в шестнадцатеричную систему и обратноосуществляется через двоичную систему с помощью триад и тетрад.
Пример. Перевести 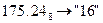 с.с.
с.с.
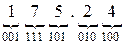
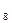
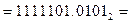
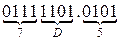
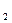
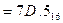
Результат: 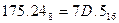 .
.
Двоичная арифметика.
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения.
| Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
| 0+0=0 0+1=1 1+0=1 1+1=10 | 0–0=0 1–0=1 1–1=0 10–1=1 | 0 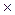 0=0 0 0=0 0 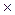 1=0 1 1=0 1 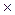 0=0 1 0=0 1 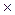 1=1 1=1 |
Пример.Выполнить сложение двоичных чисел: а) X=1101, Y=101;
X= 1101 Y=+ 101 X+Y= 10010 Результат 1101+101=10010. |
При сложениидвоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.
б) X=1101, Y=101, Z=111;
X= 1101 Y= + 101 Z= + 111 X+Y+Z=11001 Результат 1101+101+111=11001. |
При вычитаниидвоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.
Пример. Заданы двоичные числа X=10010 и Y=101. Вычислить X–Y.

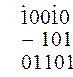
Результат 10010 – 101=1101.
Умножениедвоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.
Пример. 1001 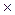 101=?
101=?
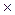 101 1001 101 1001 |
Результат 1001 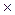 101=101101.
101=101101.
Делениедвоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.
Пример.
1100.011: 10.01=?
| 110001.1 | |
| – 1001 | 101.1 |
| – 1001 | |
| – 1001 | |
Результат 1100.011:10.01=101.1.
Упражнения 1.
1. Перевести следующие числа в десятичную систему счисления:
а) 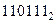 ; б)
; б) 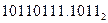 ; в)
; в) 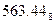 ; г)
; г) 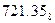 ; д)
; д) 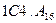 ; е)
; е) 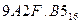 .
.
2. Перевести следующие числа из 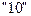 с.с в
с.с в 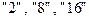 с.с.:
с.с.:
а) 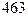 ; б)
; б) 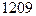 ; в)
; в) 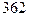 ; г)
; г) 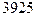 ; д)
; д) 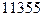 .
.
3. Перевести следующие числа из 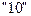 с.с в
с.с в 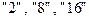 с.с. (точность 5 знаков после точки):
с.с. (точность 5 знаков после точки):
а) 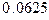 ; б)
; б) 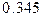 ; в)
; в) 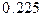 ; г)
; г) 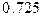 ;
;
д) 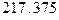 ; е)
; е) 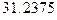 ; ж)
; ж) 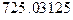 ; з)
; з) 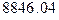 .
.
4. Перевести следующие числа в двоичную систему счисления:
а) 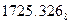 ; б)
; б) 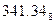 ; в)
; в) 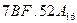 ; г)
; г) 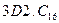 .
.
5. Перевести следующие числа из одной системы счисления в другую:
а) 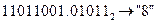 с.с.;
с.с.;
б) 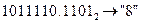 с.с.;
с.с.;
в) 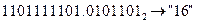 с.с.; г)
с.с.; г) 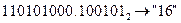 с.с..
с.с..
6. Перевести следующие числа из одной системы счисления в другую:
а) 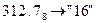 с.с.; б)
с.с.; б) 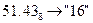 с.с.;
с.с.;
в) 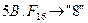 с.с.; г)
с.с.; г) 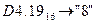 с.с..
с.с..
7. Заданы двоичные числа X и Y. Вычислить X+Y и X–Y , если:
а) X= 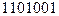 , Y=
, Y= 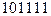 ;
;
б) X= 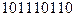 , Y=
, Y= 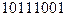 ;
;
в) X= 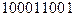 , Y=
, Y= 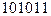 .
.
8. Заданы двоичные числа X и Y. Вычислить X*Y и X/Y , если:
а) X= 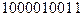 , Y=
, Y= 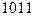 ;
;
б) X= 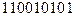 , Y=
, Y= 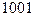 ;
;
в) X= 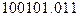 , Y=
, Y= 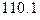 ;
;
г) X= 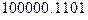 , Y=
, Y= 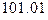 .
.
