Вычислительная сложность метода, основанного на LU-разложении матрицы системы. Сравнение LU-метода и метода Гаусса

Вспомним метод решения СЛАУ 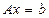, основанный на LU-разложении матрицы системы, подробно рассмотренный в лекции 7. Исходная система представляется в эквивалентном виде: 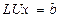. После обозначения произведения матрицы 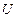на вектор неизвестных 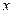через вектор новых неизвестных 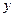( 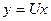), решение исходной системы 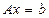сводится к последовательному решению двух треугольных систем:

1. 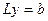; решением этой СЛАУ, матрица 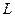которой является нижней треугольной с единицами на главной диагонали, является вектор ;

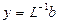2. 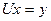. С учетом полученного на предыдущем шаге 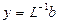, рассматриваемая система в матричном виде представляется следующим образом: 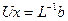. Полученная СЛАУ – это система с верхней треугольной матрицей 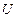. Ее решение в матричном виде: .

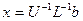Таким образом, при решении СЛАУ LU-методом сначала происходит преобразование матрицы СЛАУ (т.е. ее треугольное разложение 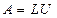), и лишь затем происходит преобразование вектора правой части (при решении первой треугольной системы 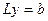получаем новый вектор правой части 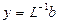для СЛАУ 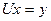, решение которой является искомый вектор ).

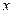Вспомним теперь матричное представление метода Гаусса без перестановок, полученное в лекции 8. Исходная СЛАУ 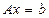постепенно преобразуется к верхнему треугольному виду путем умножения на соответствующие матрицы исключения (см.лекц.8) на каждом шаге метода Гаусса:

1 шаг метода Гаусса (исключения в первом столбце матрицы СЛАУ): ;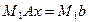

2 шаг (исключения во втором столбце матрицы СЛАУ): ;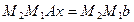

И т.д.

Последний 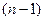-ый шаг: .

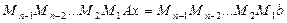Таким образом, в методе Гаусса преобразование матрицы СЛАУ и вектора правой части происходит одновременно. Получаемая в итоге матрица СЛАУ – это верхняя треуольная матрица 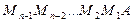. Обозначим ее 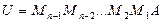. Обозначим через 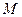произведение нижних треугольных с единицами на главной диагонали матриц исключения: 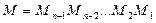. Эта матрица невырожденная, а потому из равенства 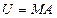следует, что 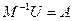, причем 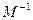- нижняя треугольная матрица с единицами на главной диагонали. Если теперь обозначить эту матрицу через 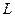, то получим известное нам треугольное разложение матрицы: 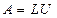, где 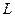- нижняя треугольная с единицами на главной диагонали, а 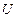- верхняя треугольная матрица, которое в соответствии с теоремой об LU-разложении определяется однозначно. СЛАУ, получаемая на последнем шаге метода Гаусса 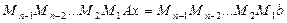запишется в виде:

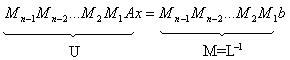
т.е. ,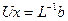

а ,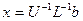

что полностью отвечает матричному виду решения СЛАУ, полученному методом, основанном на LU-разложении матрицы СЛАУ.

Таким образом, метод Гаусса без выбора главного элемента и метод решения СЛАУ, основанный на LU-разложении матрицы системы отличаются друг от друга только порядком проведения одних и тех же операций: в методе Гаусса преобразование матрицы и вектора правой части СЛАУ осуществляется параллельно (одновременно), а в методе, основанном на LU-разложении сначала преобразовывается матрица, а затем вектор правой части (последовательные преобразования), хотя сами преобразования матрицы и вктора правой части носят одинаковый характер в обоих методах. Таким образом, количество операций, необходимых для решения СЛАУ LU-методом, такое же, как и количество операций в методе Гаусса без выбора главного элемента - 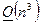. При этом само треугольное разложение матрицы СЛАУ 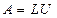требует 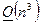операций и является наиболее трудоемким в ходе решения СЛАУ, а решение двух треугольных систем требует, как уже было показано выше, потребует 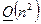операций.

Необходимо заметить, что большинство распространенных точных методов решения СЛАУ можно рассматривать как варианты метода Гаусса, вычислительная сложность которых определяется как 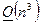, отличающиеся между собой лишь некоторыми деталями.

Как правило, метод LU-разложения используется тогда, когда нужно решить несколько систем с одной и той же матрицей. В этом случае наиболее трудоемкий в вычислительном смысле процесс LU-разложения матрицы проводится 1 раз (это 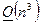операций). А решение двух треугольных систем многократно (это 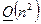операций).

Вопросы