Схема подпрограммы вычисления псевдопроекции
На рис. рис. 6 приведена схема подпрограммы вычисления псевдопроекции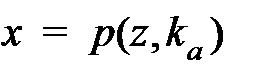 
из целевой точки 
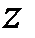на пересечение многогранника 
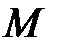с ячейкой сеточной области, имеющей порядковый номер 
, где вычисляется по формуле . Псевдопроекция вычисляется путем организации фейеровского процесса .
Рис. 6. Схема подпрограммы π вычисления псевдопроекции.
На шаге 1 выполняется инициализация переменных, необходимых для организации итерационного процесса. В качестве начального значения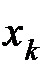 
берется точка 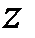; с помощью подпрограммы zero (см. рис. 4) вычисляется нулевая вершина 
ячейки с номером ; по формуле определяется вариативная часть 
расширенного столбца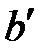 
системыограничений , получаемой при пересечении многогранника 
с ячейкой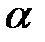 
. В цикле 2 вычисляется normsq – вектор квадратов норм строк расширенной матрицы 
: 
.
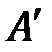На шаге 3 организуется итерационный процесс вычисления псевдопроекции. Для обеспечения высокой масштабируемости процедуры вычисления псевдопроекции используется метод разбиения вектор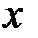а 
на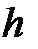 
подвекторов размерности 
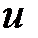, предложенный в работе [7]. Мы здесь предполагаем, что 
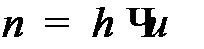. На каждом v-том подвекторе делается 
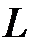независимых итераций вида
Указанная формула получается из формулы путем ограничения действия фейеровского отображения 
на соответствующий подвектор. Подпрограмма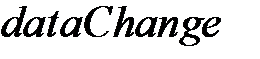 
вносит изменения в исходные данные с периодом в 
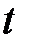секунд ( 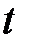– положительное число, которое может принимать значения меньше единицы).
Итерационный процесс заканчивается, когда расстояние между двумя последними приближениям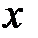и 
и 
будет меньше 
. На четвертом шаге подпрограмма 
(см. рис. 7) проверяет принадлежность найденной точки псевдопроекции 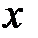ячейке с номером . Если 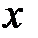не принадлежит ячейке с номером , то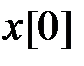 
присваивается значение 
.
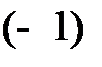Рис. 7. Схема подпрограммы in,
проверяющей принадлежность точки x ячейке с номером k𝛼.
Переменная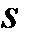 
в подпрограмме 
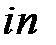на рис. 7 задает длину ребра ячейки. Ее значение определяется на шаге 11 подпрограммы 
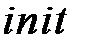(см. рис. 5.). Константа 
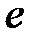задает малое положительное число, позволяющее корректно обрабатывать приближенные значения.
Модельный пример
Модельный пример имеет следующий вид.
Целевая функция 
.
Выбор начальной точки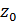 
влияет на результат (на точку псевдопроекции). Положим 
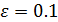при начальной точке 
мы получаем результат 
, совпадающий с точным решением. Но, для 
получаем результат 
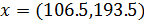. Указанная точка лежит на границе многогранника, но не является удовлетворительным приближением к точному решению.
Вывод: необходимо вычислять псевдопроекции для начальных точек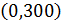 
, 
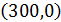и брать в качестве результата псевдопроекцию, в которой достигается максимум целевой функции.
Полученные результаты
Была написана программа на языке программирования С++ с использованием библиотеки OpenMP, реализующая сеточный алгоритм решения задачи линейного программирования (Приложение 2). Программа вычисляет решение задачи с заданной точностью. Из плюсов можно отметить возможность изменения исходных данных в процессе работы программы. Кроме того, алгоритм допускает эффективное распараллеливание на многопроцессорных системах с массовым параллелизмом. Из минусов можно отметить медленную сходимость и чувствительность к настройке параметров алгоритма.
Список литературы
1). Бердникова Е.А. Параллельный алгоритм решения задачи линейного программирования на основе оператора проектирования на линейное многообразие // Высокопроизводительные вычисления и их приложения: Труды Всероссийск. науч. конф. (30 октября - 2 ноября 2000 г., г. Черноголовка). М.: Изд-во МГУ. 2000. C. 71-72.
2). Бердникова Е.А., Ерёмин И.И., Попов Л.Д. Распределенные фейеровские процессы для систем линейных неравенств и задач линейного программирования // Автоматика и телемеханика. No. 2. 2004. С. 16-32.
3). Васин В.В., Еремин И.И. Операторы и итерационные процессы фейеровского типа. Теория и приложения. Екатеринбург: УрО РАН, 2005. 210 с.
4). Воеводин Вл.В., Капитонова А.П. Методы описания и классификации архитектур вычислительных систем. –М: Изд-во МГУ, 1994. 103 с.
5). Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. СПб.: БХВ-Петербург, 2002. 600 с.
6). Гаранжа В.А., Голиков А.И., Евтушенко Ю.Г., Нгуен М.Х. Параллельная реализация метода Ньютона для решения больших задач линейного программирования // Журнал вычислительной математики и математической физики. 2009. Т. 49. № 8. С. 1369-1384.
7). Ершова А.В., Соколинская И.М. О сходимости масштабируемого алгоритма построения псевдопроекции на выпуклое замкнутое множество // Вестник ЮУрГУ. Серия "Математическое моделирование и программирование". 2011. No. 37(254), вып. 10. C. 12-21.
8). Горелик A.Л., Гуревич И. Б., Скрипкин В. А. Современное состояние проблемы распознавания: Некоторые аспекты. М.: Радио и связь, 1985. 161 с.
Данциг Дж. Линейное программирование, его применение и обобщения. М.: Прогресс, 1966. 600 с.
9). Джексон П. Введение в экспертные системы. М: Издательский дом "Вильямс", 2001. 624 с.
10). Еремин И.И. Фейеровские методы для задач выпуклой и линейной оптимизации. Челябинск: Изд-во ЮУрГУ, 2009. 200 с.
Приложение 1
Основные обозначения для сеточного алгоритма
| Обозначение | Значение |
 | Матрица коэффициентов системы неравенств в задаче ЛП |
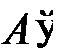 | Расширенная матрица (матрица пересечения многогранника с ячейкой 𝛼); имеет размер  ; получается из A путем приписывания снизу коэффициентов неравенств системы |
 | столбец свободных членов (правых частей) неравенств |
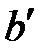| | расширенный столбец (столбец правых частей пересечения многогранника с ячейкой 𝛼); имеет размер 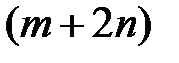 получается из b путем приписывания снизу вектора правых частей неравенств системы |
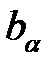 | вариативная часть расширенного столбца 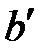системы ограничений , получаемой при пересечении многогранника с ячейкой . |
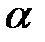| c | вектор коэффициентов целевой функции |
| C | максимум значений целевой функции |
| dataChange(t) | подпрограмма изменения исходных данных с периодом в t секунд (t может принимать значения меньше 1) |
| σ | значение целевой функции в точке xk |
| ε | точность приближения при вычислении псевдопроекции (используется следующий критерий завершения фейеровского процесса:  ) |
| g | нулевая вершина кубической сеточной области |
| G | начальные координаты нулевой вершины g кубической сеточной области |
| γ | целочисленные координаты центральной ячейки |
| init | подпрограмма инициализации переменных |
| factor | множитель  в формуле фейеровского отображения |
| k | порядковый номер ячейки |
| kγ | порядковый номер центральной ячейки |
| k𝛼 | порядковый номер ячейки 𝛼, на которой достигается максимум целевой функции; k𝛼 = MinInt соответствует случаю, когда получено пустое множество псевдопроекций |
| K | количество ячеек в сеточной области по одному измерению |
| L | число независимых фейеровских итераций на подвекторах |
| m | число неравенств в системе ограничений |
| MinFloat | минимальное вещественное число, представляемое в машинной форме |
| MinInt | минимальное целое число, представляемое в машинной форме |
| n | размерность пространства решений |
| normsq | вектор квадратов норм строк матрицы : |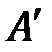
| p | количество итераций при построении псевдопроекции, выполняемое между обновлениями входных данных |
| P | количество MPI-процессов |
| π(z, k) | подпрограмма вычисления псевдопроекции точки z на пересечение многогранника с ячейкой, имеющей порядковый номер k; возвращает точку псевдопроекции xk или вектор (-1,…), если точка псевдопроекции не принадлежит многограннику |
| q | нулевая вершина центральной ячейки сеточной области |
| q' | нулевая вершина новой центральной ячейки сеточной области |
| r | длина ребра сеточной области |
| R | начальное значение r, обеспечивающее покрытие многогранника сеточной областью |
| rank() | системная функция, возвращающая количество MPI-процессов |
| s | шаг сетки:  |
| T | масштабирующий коэффициент для вычисления координат целевой точки z |
| w | мультипликативный коэффициент для увеличения размера сеточной области |
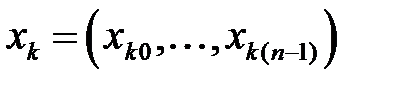 | псевдопроекция на пересечение многогранника с k-той ячейкой; если  , то пересечение многогранника с k-той ячейкой пусто |
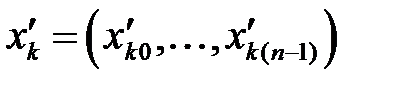 | предыдущая точка в фейеровском процессе |
| y | нулевая вершина ячейки 𝛼 |
| z | целевая точка |
| zero(k) | вектор-функция, вычисляющая нулевую вершину ячейки с порядковым номером k |
Приложение 2
Код программы
#include "include.h"
using namespace std;
int main(int argc, char *argv[]) {
LoadData(); // Загрузка исходных данных из файла input.txt
Init(); // Инициализация переменных
Pi(/*axis*/ 0 ,/*index*/ 0); // Вычисление точки псевдопроекции _x из _z на пересечение с ячейкой с индексом index на оси с номером axis
cout << "x="; for (int j = 0; j<_n; j++) cout << _x[j] << "\t"; cout << endl; fflush(stdout);
printf("\nPress ENTER"); fflush(stdout); getchar();
return 0;
};
static void Init() {// Инициализация переменных
_mc = _m + _n * 2; // Количество неравенств в расширенной системе
assert(_MAX_MC >= _mc);
#ifndef _NO_MPI
MPI_Init(&argc, &argv); // старт MPI
MPI_Comm_rank(MPI_COMM_WORLD, &_rank); // присвоить _rank номер процесса MPI
MPI_Comm_size(MPI_COMM_WORLD, &_size); // присвоить _size количество процессов MPI
#else
_rank = 0;
#endif
// Добавляем кубик в А
for (int i = 0; i<_n; i++)
_A[i + _m][i] = -1;
for (int i = 0; i<_n; i++)
_A[i + _m + _n][i] = 1;
_r = _R; // радиус сеточной области
_s = _r / ((_K-1)/2); // длина ребра ячейки
for (int i = 0; i < _n; i++) // координаты целевой точки
_z[i] = _c[i] * _T;
};
static void LoadData() {// Загрузка исходных данных из файла input.txt
FILE *stream;
fpos_t pos;
errno_t errNo = fopen_s(&stream, _INPUT, "r");
if (errNo != 0) {
cout << "File '" << _INPUT << "' not found!" << endl;
#ifndef _NO_MPI
MPI_Finalize();
#endif
printf("\nPress ENTER"); fflush(stdout); getchar();
abort();
};
SkipComments(stream, &pos);
fscanf_s(stream, "%d", &_n); // считываем размерность пространства решений
assert(_n <= _MAX_N);
assert(_n>0);
SkipComments(stream, &pos);
fscanf_s(stream, "%d", &_m);// считываем общее кол-во неравенств (включая -x_j<=0)
assert(_m <= _MAX_M);
assert(_m>0);
SkipComments(stream, &pos);
for (int i = 0; i<_m; i++) // Считываем матрицу А (включая -x_j<=0)
for (int j = 0; j<_n; j++)
fscanf_s(stream, "%lf", &_A[i][j]);
SkipComments(stream, &pos);
for (int i = 0; i<_m; i++) // Считываем столбец b (включая -x_j<=0)
fscanf_s(stream, "%lf", &_b[i]);
SkipComments(stream, &pos);
for (int j = 0; j<_n; j++) // Считываем вектор целевой функции c
fscanf_s(stream, "%lf", &_c[j]);
SkipComments(stream, &pos);
for (int j = 0; j<_n; j++) // Считываем координаты центральной точки звездообразной области
fscanf_s(stream, "%lf", &_g[j]);
SkipComments(stream, &pos);
fscanf_s(stream, "%lf", &_R); // Cчитываем начальное значение радиуса сеточной области, обеспечивающее покрытие многогранника
SkipComments(stream, &pos);
fscanf_s(stream, "%d", &_K); // Cчитываем количество ячеек в сеточной области по одному измерению
assert(_K>0);
assert(_K % 2 == 1);
SkipComments(stream, &pos);
fscanf_s(stream, "%d", &_L); // Cчитываем число независимых фейеровских итераций в подпрограмме вычисления псевдопроекции
SkipComments(stream, &pos);
fscanf_s(stream, "%lf", &_T); // Cчитываем масштабирующий коэффициент для вычисления координат целевой точки _z
fclose(stream);
};
static void SkipComments(FILE *stream, fpos_t *pos) {
/* Пропускает пустые строки и комментарии (строки, начинающиеся с '%') */
fscanf_s(stream, "\n");
fgetpos(stream, pos);
while (getc(stream) == '%') {
while (getc(stream) != 10);
fscanf_s(stream, "\n");
fgetpos(stream, pos);
};
fsetpos(stream, pos);
};
static void Pi(int axis, int index) { // Вычисление точки _x псевдопроекции из _z на пересечение с ячейкой с индексом index на оси с номером axis
#define b_alpha(i) _b[i+_m] // вариативная часть расширенного столбца b'
Point x_stroke; // предыдущая точка в фейеровском процессе
double S[_MAX_N]; // сумма из формулы фейеровского отображения
double _Scal_ai_x[_MAX_MC]; // Вектор A' Scal _x
double factor; // множитель в формуле фейеровского отображения
double dist; // Расстояние между соседними итерациями
//#pragma omp parallel num_threads(4)
//#pragma omp parallel for simd
for (int j = 0; j < _n; j++)
_x[j] = _z[j];
Zero(axis, index);
for (int i = 0; i < _n; i++)
b_alpha(i) = -_y[i];
for (int i = 0; i < _n; i++)
b_alpha(i + _n) = _y[i] + _s;
CalcNormsq();
// Фейеровский процесс
do {
//#pragma simd
for (int l = 0; l < _L; l++) {
for (int j = 0; j < _n; j++) {
x_stroke[j] = _x[j];
S[j] = 0;
};
for (int i = 0; i<_mc; i++) {
_Scal_ai_x[i] = 0;
for (int j = 0; j<_n; j++) // Вычисление вектора A' Scal _x
_Scal_ai_x[i] += _A[i][j] * _x[j];
factor= __max(_Scal_ai_x[i] - _b[i], 0) / _normsq[i];
for (int j = 0; j < _n; j++)
S[j] += factor*_A[i][j];
};
for (int j = 0; j < _n; j++)
_x[j] = x_stroke[j] - (_lambda / _m)*S[j];
};
DataChange(); // Подпрограмма изменения исходных данных
dist = Dist(_x, x_stroke);
}while (dist>_EPS_F);
};
static void CalcNormsq() { // Вычисление столбца квадратов норм a_i
for (int i = 0; i<_mc; i++) {
double s = 0;
for (int j = 0; j<_n; j++)
s += _A[i][j] * _A[i][j];
_normsq[i] = s;
};
};
static void Zero(int axis, int index) { // Вычисление нулевой вершины y[*] ячейки с индексом index на оси с номером axis
assert(axis >= 0 && axis<_n);
assert(abs(index) < (_K - 1) / 2);
for (int j = 0; j < _n; j++)
_y[j] = _g[j];
_y[axis] = _g[axis] + index*_s;
};
static void DataChange() {};
static double Dist(Point x1, Point x2) { // Расстояние между точками
double x, dist;
dist = 0;
for (int j = 0; j<_n; j++) {
x = x1[j] - x2[j];
dist += x*x;
};
dist = sqrt(dist);
return dist;
};
[1]) С помощью символа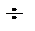 
здесь обозначается целочисленное деление.