Методические указания по организации самостоятельной работы студентов

Такой прием не является эффективным. Поэтому на практике чаще всего используют специальные алгоритмы умножения чисел в дополнительных кодах. Алгоритмы корректного умножения операндов в ( ) можно разделить на две группы:

- алгоритмы первой группы это алгоритмы с обработкой знаковых разрядов отдельно от числовых;

- алгоритмы второй группы это алгоритмы с обработкой знаковых разрядов вместе с числовыми. Т.е., на сумматоре дополнительных кодов в процессе перемножения машинных изображений операндов получают одновременно знаковую и числовую части произведения.

Теорема: произведение дополнительных кодов сомножителей равно дополнительному коду результата только в случае положительных сомножителей.

Если хотя бы один сомножитель отрицателен, то произведение чисел на сумматоре дополнительных кодов получается прибавлением поправки ( 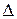) к произведению дополнительных кодов сомножителей.

Рассмотрим арифметическое обоснование алгоритмов первой группы при различных вариантах комбинаций знаков операндов. С этой целью у операндов отбрасывается знаковая цифра и выполняется умножение полученных псевдомодулей по одному из известных алгоритмов. Результат такого умножения назовем псевдопроизведением ( ).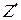

Обозначим вес знакового разряда сомножителей ( ).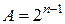

Тогда, в соответствии с рассмотренным ранее правилом формирования дополнительного кода, отрицательные сомножители будут представлены в ( ) следующим образом:

.

.

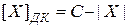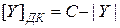При удалении знакового разряда получаем псевдомодули:

.

.

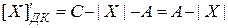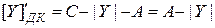Всего возможны четыре варианта сочетания знаков сомножителей:

Случай №1.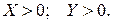

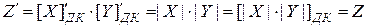
В этом случае сразу получено истинное значение положительного произведения в ( ), которое не требует корректирования.

Случай №2.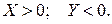

.

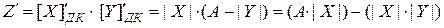Результат значительно отличается от модуля кода истинного произведения:

.

.

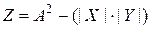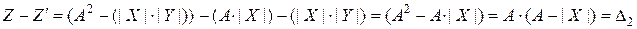Сомножитель 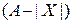представляет собой ( 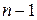) - разрядный псевдомодуль числа ( 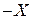), представленного в ( ).

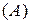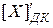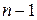Сомножитель эквивалентен сдвигу на ( ) разряд влево.

Сравнение ( 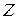) и ( 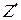) показывает, что результат умножения должен быть скорректирован посредством сложения ( 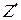) с поправкой ( ).

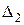Случай №3.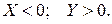

.

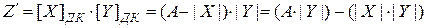
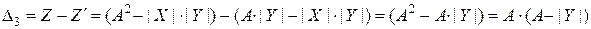Случай №4.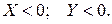

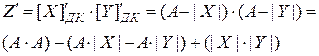
Тогда истинное произведение ( 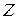) равно:

.

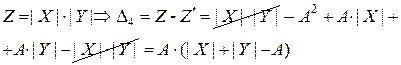На практике используют упрощенную поправку 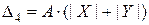, поскольку нескорректированный операнд ( 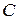) проявит себя в виде ( 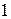) в знаковом разряде. Это не имеет значения, поскольку знак ( 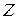) был сформирован отдельно на начальном этапе. Подход к формированию алгоритма умножения состоит в следующем:

1. Получим псевдомодули операндов, отбросив старшие (знаковые) цифры: ( 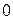) - в положительном числе, ( 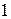) - в отрицательном.

2. Считая разрядную сетку наращиваемой, видим, что операнд в старших разрядах содержит незначащие цифры, тождественно равные знаковой.

3. В таком случае истинные операнды можем считать «удлиненными псевдомодулями», у которых самые левые цифры играют роль знаковых разрядов.

4. Выполняя их умножение по правилам, рассмотренным выше, получаем уже не модуль ( 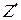), а само псевдопроизведение с некоторыми псевдознаковыми цифрами в двух самых старших разрядах. Указанные цифры относятся к знаковым по расположению, но не имеют смысла таковых.

5. Возникает задача найти истинное значение знаковой цифры числа ( ).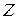

Рассмотрим арифметическое обоснование алгоритмов второй группы при различных вариантах комбинаций знаков операндов, т.е. умножение чисел в ( ) с обработкой знаковых разрядов вместе с числовыми в зависимости от сочетания знаков сомножителей. При этом используем предпосылки, приведенные в предыдущем доказательстве. Считаем, что вес знакового разряда равен ( 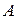). Тогда вес разряда, следующего за знаковым: .

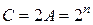Случай №1.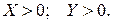

Перемножая машинные представления сомножителей в ( ), получим:

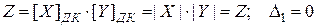
Случай №2.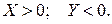

Учитывая, что разрядность произведения (и псевдопроизведения) составит ( 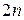) - бит, вес разряда, следующего за знаковым разрядом произведения:

.

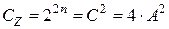Тогда:

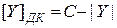
Перемножая сомножителей, получим:

.

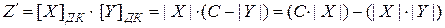Истинное значение произведения получается:

.

.

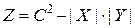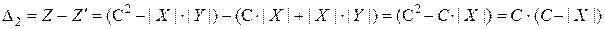Случай №3.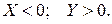

Аналогично предыдущему можно показать, что данному варианту требуется коррекция:

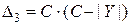
Случай №4.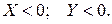

.

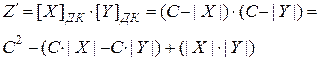
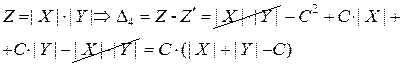На практике используют упрощенную поправку:

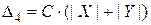
При умножении в ( ) по любому из вариантов данной группы в процессе прибавления ( 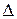) к ( 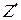) важно соблюдать соответствие весов разрядов псевдопроизведения и корректирующей поправки (с учетом наличия псевдознака). Старший разряд корректирующей поправки сформирует знаковую цифру. Из рассмотренных ранее вариантов умножения в соответствии с алгоритмами обеих групп, следует, что для коррекции результата умножения ( ) операндов необходимо в каждом случае по комбинации знаков определять величину коррекции, а затем выполнять 1-2 шага суммирования.

Однако этого можно избежать, если коррекцию совмещать с процессом суммирования частичных произведений. Рассмотренные алгоритмы являются базовыми и реализуют непосредственный способ введения поправок. Более широкое применение на практике получили алгоритмы с косвенным способом введения поправок.

Случай №1.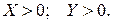

По примеру первой и второй групп результат является истинным произведением и корректировка не требуется. Т.е. сформированы истинные модуль и знак.

Случай №2.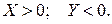

При умножении младшими разрядами вперед получится известный для этого случая модуль псевдопроизведения. Если при умножении на знаковую цифру множителя не прибавлять последнее ( 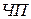) к их сумме, а вычесть его, тем самым, ( 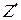) будет уменьшено на ( ).

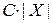Кроме того, если для представления последнего ( 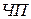) воспользоваться ( ), то при его прибавлении не только будет откорректирована числовая часть произведения, но и сформируется правильный его знак.

При этом, последний сдвиг ( 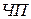) должен быть арифметическим с учетом отрицательного знака ЧП.

Случай №3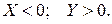

Если сдвиг суммы ( 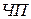) вправо на ( 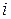) разрядов выполнять по правилам сдвига модифицированного ( ), а затем выполнять суммирование ( 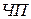) по правилам суммирования модифицированных ( ) (с потерей переноса из знакового разряда), то будет получено правильное произведение исходных чисел в ( ), т.е. ( ).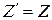

Т.о., коррекция не требуется.

Случай №4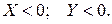

Коррекция результата выполняется объединением двух предыдущих вариантов, т.е. при умножении на знаковый разряд множителя выполняют вычитание, а суммирование и сдвиг частичных произведений производят с использованием ( ).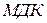

Таким образом при положительном множителе умножение в ( ) можно выполнять по алгоритмам умножения в ( 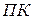), если только суммировать ( 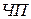) и сдвиг выполнять по правилам сложения и сдвига модифицированного ( ) (перенос из ( 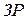) будет игнорироваться).

Существует еще один способ умножения знаковых чисел в ( ).

Он заключается в том, что отрицательный множитель необходимо преобразовать в положительный.

Это выполняется умножением на ( 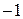) множимого и множителя.

В итоге, в соответствии с выше приведенной теоремой, умножение выполняется по обычным правилам, а результат не нуждается в корректировке.

Общий алгоритм умножения целых двоичных знаковых чисел, представленных в ( ), заключается в следующем:

1. Исходное значение суммы ( 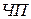) принимается равным ( 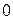), ( ) 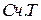присваивается значение равное числу разрядов множителя.

2. Анализируется младшая разрядная цифра множителя. Если она равна ( 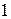), то к сумме ( 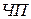) прибавляется множимое; если ( 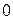) - прибавление не производится. Множимое при этом совмещается с суммой ( 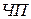) по старшим разрядам и представлено в исходном коде.

3. Производится арифметический сдвиг суммы ( 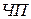) вправо на ( 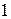) разряд с учетом флагов переноса ( 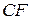) и переполнения ( 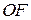). Содержимое ( 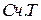) уменьшается на ( ).

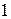4. пп.2-3 последовательно выполняются для всех цифровых разрядов множителя.

5. Если множитель - положительное число, то полученный результат является истинным произведением ( 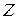). Если множитель - отрицательное число, то к полученному результату ( 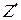) прибавляется множимое с обратным знаком (дополнение), совмещенное по старшим разрядам. Полученная сумма представляет собой истинное произведение ( 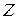). . 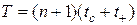где ( 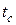) - время, затрачиваемое на выполнение операции сдвига на один разряд; ( 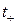) - время, затрачиваемое на выполнение операции сложения.

Так как данные в памяти компьютера хранятся в ( ), операцию деления целесообразно выполнять в ( ). За основу можно принять базовый алгоритм деления ( без восстановления остатка), т.к. он предполагает использование отрицательного делителя, дополнительного кода для вычитания и учет знаков остатка и делителя на каждом шаге деления. Делимое участвует в операции только на первом шаге, а далее используются остатки, которые могут быть как положительными, так и отрицательными. Поэтому не имеет смысла рассматривать алгоритмы деления в ( ), где знаки операндов обрабатываются отдельно от их числовых частей. Таким образом, при делении чисел в ( ) трудности, связанные с коррекцией результата (как при умножении в дополнительном коде), практически отсутствуют.

Пусть:

.

.

.

.

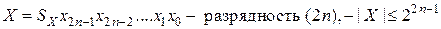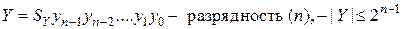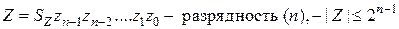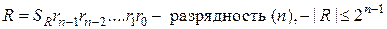Для проверки на корректность операции деления используется условие:

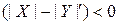. Таким образом, при пробном вычитании делитель должен быть сдвинут на ( 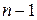) разряд влево.

Однако чтобы обеспечить регулярность процесса деления, делитель сдвигается влево на ( 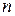) разрядов, а перед пробным вычитанием делимое сдвигается на один разряд влево.

В каждом цикле сдвинутый остаток складывается с делителем, которому приписывается знак, противоположный знаку частичного остатка.

Алгоритм деления знаковых чисел отличается от алгоритма деления беззнаковых чисел способом формирования разрядных цифр частного.

Очередная цифра определяется на основе анализа знаков частичного остатка и делителя. Если знак полученного остатка совпадает со знаком делителя, то цифра частного равна ( 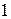), если нет - ( ).

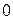При этом частное формируется в прямом или обратном коде (в зависимости от соотношения знаков делимого и делителя).

На этапе пробного вычитания автоматически формируется старшая цифра частного, которая представляет его знак.

Если знак полученного частичного остатка совпадает со знаком делителя, участвующего в операции пробного вычитания, деление является корректным. В противном случае имеет место переполнение разрядной сетки компьютерной системы.

Алгоритм деления целых двоичных знаковых чисел заключается в следующем:

1. Частному присваивается значение ( 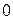), ( ) 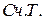- ( )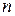. Исходное значение частичного остатка равно ( 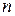) старшим разрядам делимого.

2. Частичный остаток удваивается сдвигом влево на ( 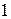) разряд, с занесением в младший разряд очередной цифры делимого.

3. Если частичный остаток и делитель разного знака, то они складываются, если же одного знака, то из частичного остатка вычитается делитель.

4. Частное сдвигается влево на ( 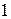) разряд. В освобождающийся младший разряд заносится очередная цифра частного: ( 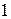) - если знак делителя и остатка совпадают, ( 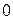) - в противном случае ( 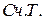) уменьшается на ( ).

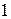5. Пункты 2-4 повторяются до тех пор, пока ( 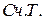) не станет равным ( ).

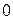6. Частное и остаток сформированы в обратном коде. Если знак окончательного остатка не совпадает со знаком делимого, то выполняется его восстановление. Для получения ( ) результата выполняется его коррекция в зависимости от соотношения знаков делимого и делителя.

При делении в дополнительном коде возможные комбинации знаков операндов образуют следующий перечень.

Случай №1. 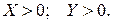Деление в этом случае ничем не отличается от деления положительных операндов в прямом коде. Коррекция не требуется.

Случай №2. 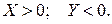Этот случай легко сводится к обычному делению в прямом коде, если считать, что в наличии имеется .

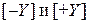Однако для формирования правильного знака частного и обратного кода отрицательного результата необходимо псевдознаковую цифру и цифры частного получать равными цифрам знаковых разрядов соответствующих остатков.

Переполнение разрядной сетки здесь фиксируется по ( 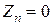). В конце деления для образования дополнительного кода и округления частного следует прибавить единицу к младшему разряду: ( ).

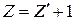Случай №3. 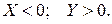Из отрицательного делимого должен вычитаться положительный делитель, в отличие от деления без восстановления остатка в прямом коде, когда на первом шаге ( 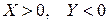). Поэтому псевдознаковая цифра частного ( 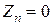), полученная по знаку нулевого остатка в соответствии с алгоритмом деления без восстановления остатка, здесь указывает на переполнение разрядной сетки. Если же переполнения разрядной сетки нет, эта цифра является правильной знаковой цифрой частного (то есть, 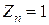). Знаки всех других остатков в этом случае определяют инверсные значения цифр частного. В результате будет записан обратный код отрицательного частного. Для округления и получения дополнительного кода результата необходимо добавить единицу в младший разряд, если полученный остаток не равен нулю: ( ).

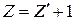Случай №4. 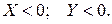На первом шаге алгоритма для формирования правильного знака частного ( 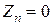), необходимо из отрицательного делимого вычитать отрицательный делитель ( 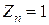соответствует переполнению разрядной сетки).

Далее же этот случай сводится к третьему. Здесь все цифры частного, включая псевдознаковую, равны знакам остатков. В случае, когда полученный остаток равен нулю, к частному следует прибавить единицу ( 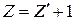). При использовании методов с восстановлением остатка и без восстановления остатка сдвиг влево может вызвать передачу значащей цифры из старшего разряда остатка в знаковый, и остаток будет искажен.

Поэтому надо оперировать двумя знаковыми разрядами.

Правильный знак при этом находится в дополнительном знаковом разряде, а единица в основном относится к разряду переполнения (в случае правильных дробей - к разряду целых). Знак остатка от деления должен совпадать со знаком делимого.

Контрольные вопросы

1. Объясните прицип работы логического сдвига.

2. Объясните принцип работы арифметического сдвига.

3. Объясните принцип работы модифицированного сдвига.

4. Объясните принцип работы циклического сдвига.

5. Сформулируйте алгоритм умножения младшими разрядами вперед, со сдвигом суммы ( 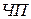) вправо двоичных знаковых чисел.

6. Сформулируйте алгоритм деления целых двоичных знаковых чисел методом без восстановлением остатка