Задания 3.2 для самостоятельной проработки

Составить программу вычисления суммы ряда с заданной точностью e. Анализируя код программы, выявить возможные причины возникновения исключений и ввести их обработку, обеспечивающую вывод типа исключения и пояснение к причине его возникновения.

1.Вычислить с точностью e

- приближенное значения функции ln(1+X)/X по формуле
,
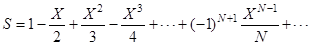используя смешанный способ вычисления члена ряда,

- точное значение функции ln(1+X)/X,

- абсолютную и относительную ошибки приближенного значения.

2.Вычислить с точностью e

- приближенное значения функции 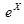по формуле
,
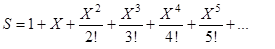используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,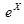

- абсолютную и относительную ошибки приближенного значения.

3.Вычислить с точностью e

- приближенное значения функции sinX по формуле
,
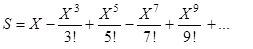используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции sinX,

- абсолютную и относительную ошибки приближенного значения.

4.Вычислить с точностью e

- приближенное значения функции 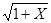по формуле
,
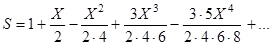используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,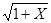

- абсолютную и относительную ошибки приближенного значения.

5.Вычислить с точностью e

- приближенное значения функции arcsinX по формуле
,
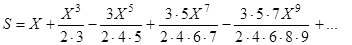используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции arcsinX,

- абсолютную и относительную ошибки приближенного значения.

6.Вычислить с точностью e

- приближенное значения функции arctgX по формуле
,
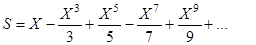используя смешанный способ вычисления члена ряда,

- точное значение функции arctgX,

- абсолютную и относительную ошибки приближенного значения.

7.Вычислить с точностью e

- приближенное значения функции 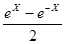по формуле
,
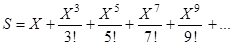используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,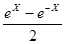

- абсолютную и относительную ошибки приближенного значения.

8.Вычислить с точностью e

- приближенное значения функции 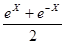по формуле
,
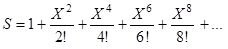используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,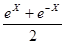

- абсолютную и относительную ошибки приближенного значения.

9.Вычислить с точностью e

- приближенное значения функции ln(1-X) по формуле
,
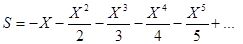используя смешанный способ вычисления члена ряда,

- точное значение функции ln(1-X),

- абсолютную и относительную ошибки приближенного значения.

10.Вычислить с точностью e

- приближенное значения функции 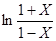по формуле
,
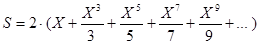используя смешанный способ вычисления члена ряда,

- точное значение функции ,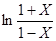

- абсолютную и относительную ошибки приближенного значения.

11.Вычислить с точностью e

- приближенное значения функции 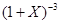по формуле
,
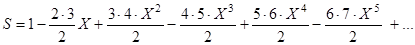используя смешанный способ вычисления члена ряда,

- точное значение функции ,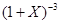

- абсолютную и относительную ошибки приближенного значения.

12.Вычислить с точностью e

- приближенное значения функции 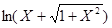по формуле
,
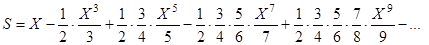используя смешанный способ вычисления члена ряда,

- точное значение функции ,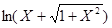

- абсолютную и относительную ошибки приближенного значения.

13.Вычислить с точностью e

- приближенное значения функции 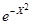по формуле
,
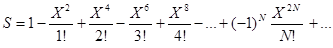используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,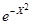

- абсолютную и относительную ошибки приближенного значения.

14.Вычислить с точностью e

- приближенное значения функции 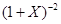по формуле
,
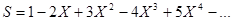используя смешанный способ вычисления члена ряда,

- точное значение функции ,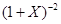

- абсолютную и относительную ошибки приближенного значения.

15.Вычислить с точностью e

- приближенное значения функции 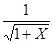по формуле
,
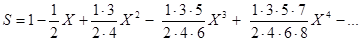используя рекуррентную формулу для вычисления члена ряда,

- точное значение функции ,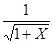

- абсолютную и относительную ошибки приближенного значения.

16.Вычислить с точностью e

- приближенное значения π по формуле
,
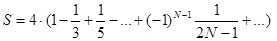используя смешанный способ вычисления члена ряда,

- точное значение π с помощью стандартной функции Pi,

- абсолютную и относительную ошибки приближенного значения.

17.Вычислить с точностью e

- приближенное значения 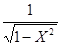по формуле
,
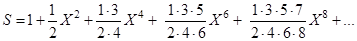используя рекуррентную формулу для вычисления члена ряда,

- точное значение 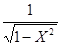функции,

- абсолютную и относительную ошибки приближенного значения.

18.Вычислить с точностью e сумму бесконечного ряда

,

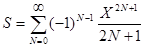- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

19.Вычислить с точностью e сумму бесконечного ряда

,

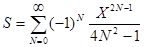- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

20.Вычислить с точностью e сумму бесконечного ряда

,

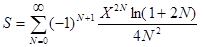- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

21.Вычислить с точностью e сумму бесконечного ряда

,

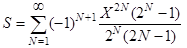- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

22.Вычислить с точностью e сумму бесконечного ряда

,

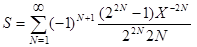- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

23.Вычислить с точностью e сумму бесконечного ряда

,

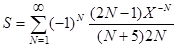- используя смешанный способ вычисления члена ряда,

- используя общую формулу для вычисления члена ряда.

24.Вычислить с точностью e сумму бесконечного ряда

,

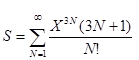- используя смешанный способ вычисления члена ряда,

- используя рекуррентную формулу для вычисления члена ряда.

25.Вычислить с точностью e сумму бесконечного ряда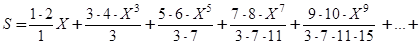

,

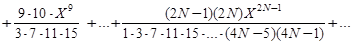- используя смешанный способ вычисления члена ряда,

- используя рекуррентную формулу для вычисления члена ряда.

26.Вычислить с точностью e сумму бесконечного ряда ,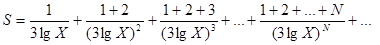

используя смешанный способ вычисления члена ряда.

27. Вычислить с точностью e сумму бесконечного ряда
,

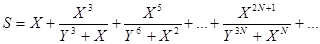- используя рекуррентную формулу для вычисления члена ряда,

- используя смешанный способ вычисления члена ряда.