Задания 4.2 для самостоятельной проработки
Составить программу для вычисления экстремума функции на заданном интервале с заданной точностью. 1) Найти аналитическое выражение для первой производной заданной в таблице функции. Одним из известных методов уточнения корня уравнения найти значение аргумента на заданном интервале, при котором первая производная обращается в ноль. Вычислить значение функции в полученной точке. С помощью второй производной определить вид экстремума (максимум или минимум) 2) Найти с помощью итерационного алгоритма экстремум той же функции и значение аргумента, при котором он достигается.
Обеспечить ввод в программе значения точности, значений, определяющих интервал поиска экстремума, начальный шаг изменения аргумента. Для обоих вариантов поиска экстремума вывести значение аргумента, при котором достигается экстремум функции, и значение функции в полученной точке.
| Номер варианта | Функция | Интервал поиска экстремума |
| X2 +1/X2 | [0,2; 2] | |
| X3 - X2 – 6X | [-2;0] | |
| cos(2x)/2 – sin(x) +2 | [π/3;2π/3] | |
X+2 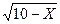 | [0;10] | |
| 3X4 -8X3 +6 X2 +2 | [0,1;2] | |
| cos(2x)-2cos(x) | [-π/6;π/3] | |
| 5x -4X | [0;2] | |
| X3 - X2 – 6X | [0; 3] | |
| X4 -8X2 -9 | [-1;1] | |
| (4x +4-x )/ln(4) | [-1;2] | |
| 2X2 +7|X-4| +5 | [-1;2] | |
X2 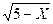 | [1;5] | |
| X2 +|X-4| | [-3;3] | |
| 1/( X2 + X +2) | [-2;2] | |
| 2X3 +15X2 +36X -30 | [-4;-2,4] | |
| X4 -6X3 +8 | [1;6] | |
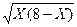 | [0,6] | |
| X3 -5X2 +3X | [1,5;5] | |
| 2X3 -3X2 | [-2;0,5] | |
| log2 ( X2 -2 X +5) | [0,2;2] | |
| 6X - X2 -6 | [0;6] | |
| log3 ( 2 X +3- X2) | [0;2] | |
| X4 -8X2 -9 | [-4;-0,5] | |
| 3X4 -8X3 +6 X2 +2 | [-2;0,1] | |
| cos(2x)/2 – sin(x) +2 | [-π/3;9π/10] | |
| 2X3 +15X2 +36X -30 | [-2,4;0] | |
| X3 -5X2 +3X | [-1;1] | |
| 2X3 -3X2 | [0,5;3] | |
| X4 -8X2 -9 | [0,2;3,5] | |
| log2 (3- 4X - 4X2) | [-1,2;0] | |
0,5x 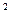 -2x -2x | [0;2] | |
| 8x -6*4x -3*2x | [0;3] | |
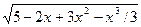 | [0;2,5] | |
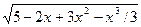 | [2,5;4] |
Обработка матриц
Матрицыпредставляют собой один из наиболее удобных математических объектов, обработка которых ведет к необходимости программирования вложенных циклов. При программной реализации обработки матриц будем использовать двумерные массивы(элементы которых имеют два индекса), считая, что элементы Хij матрицы Х, i=1, 2,...,m, j=1, 2,…,n размещаются в ячейках соответствующего массива с такими же индексами. Это позволит сделать текст программы удобным для понимания процесса обработки и уменьшить, в некоторых случаях, объём вычислений. Соответственно первый индекс массива будем называть номером строки, а второй – номером столбца.
Имея в виду соответствие элементов матрицы элементам массива, им дают, как правило, одинаковые имена; иногда в пояснениях к программе вместо термина «массив» будем использовать термин «матрица», как бы отождествлять объекты предметной области с объектами программы для лучшего понимания процессов обработки.
При постановке задач на обработку матриц с целью обеспечения применимости программ для обработки матриц, например, матрицы Х, размеры которых не должны превосходить заданных значений, например, m£12 и n£14, будем использовать сокращенное обозначение, например, Х(m,n), m£12, n£14. Указанные в таком обозначении максимальные значения индексов матрицы будут использоваться в объявлении типа соответствующего двумерного массива, а сами эти максимальные значения индексов желательно объявить в виде именованных констант. Если также учесть, что двумерный массив можно рассматривать и объявлять как одномерный массив с базовым типом массив, то объявление типа массива для хранения матриц с размерами, не превышающими 12х14 будет следующим.
const
mMax=12; nMax=14;
type
//Объявление типа строки двумерного массива типа tM
tV=array[1..mMax] of Real;
//Объявление типа двумерного массива
tM=array[1..nMax] of tV;
(при объявлении типа двумерного массива необходимо задавать тип обоих индексов и тип самих элементов матрицы).
Такое двухэтапное объявление типа двумерного массива удобно тем, что строка массива будет совместима по присваиванию с одномерным массивом того же типа tV.
Задание в разделе констант максимальных значений для количества строк и столбцов улучшает стиль программирования, так как в случае необходимости изменения количества строк или столбцов программисту не придется внимательно изучать весь текст программы, а достаточно будет изменить значения соответствующих констант.
Переменная-двумерный массив объявляется в разделе объявления переменных
var
X:tM;
Менее предпочтительными, но допустимыми будут объявления типа
tM=array[1..mMax, 1..nMax] of Real;
или
tM=array[1..12, 1..14] of Real;
и объявление массива одной строкой
var
X:array[1.. mMax, 1..nMax] of Real;
или
X:array[1..12, 1..14] of Real;
Последние варианты оказывается менее предпочтительны, так как при использовании в подпрограммах типизированных параметров, представляющих матрицы и векторы, без предварительного объявления используемых типов обойтись невозможно.
При работе с матрицами надо помнить, что первый индекс соответствует номеру строки, а второй индекс – номеру столбца.
Ввод-вывод матриц можно осуществить только с использованием вложенного цикла. Обычно принято вводить матрицу в виде матрицы, т.е. по строкам как это принято записывать на бумаге. В этом случае во внутреннем цикле должен обеспечиваться ввод (вывод) одной строки матрицы. Внешний цикл будет задавать ввод (вывод) всех строк матрицы и переход в начало новой строки после ввода (вывода) очередной строки.
Фрагмент программы, обеспечивающей ввод и вывод матрицы Х(m,n), m£12, n£14, ранее описанной, имеет следующий вид:
WriteLn('Введите количество строк и столбцов матрицы');
ReadLn(M,N);
WriteLn('Введите элементы матрицы по строкам');
for I:=1 to M do //Цикл ввода всех строк матрицы
begin
for J:=1 to N do //Цикл ввода очередной строки матрицы
Read(X[I,J]);
ReadLn; //Переход в начало новой строки файла ввода
end;
WriteLn('Введенная матрица');
for I:=1 to M do //Цикл вывода всех строк матрицы
begin
for J:=1 to N do //Цикл вывода очередной строки матрицы
Write(X[I,J]:6:1, ' ');
WriteLn; //Переход в начало новой строки файла вывода
end;
Порядок расположения циклов при вводе/выводе имеет существенное значение. Если поменять местами заголовки циклов, то вводимые значения будут присваиваться элементам столбца, а не элементам строки. При выводе матрицы в этом случае будет выведена фактически транспонированная матрица
Также надо соблюдать аккуратность при использовании приемов программирования. Например, при вычислении сумм и произведений надо следить за тем, в каком месте программы присваиваются начальные значения соответствующим переменным.
Следующий фрагмент программы позволяет вычислить сумму и произведение всех элементов матрицы:
S:=0; Pr:=1;
for I:=1 to M do
for J:=1 to N do
begin
S:=S+A[I,J];
Pr:=Pr*A[I,J];
end;
WriteLn('s=',S:8:2, ' pr=',Pr:8:2);
При изменении места расположения операторов присваивания S:=0; Pr:=1; смысл вычислений меняется:
for I:=1 to M do
begin
S:=0; Pr:=1;
for J:=1 to N do
begin
S:=S+A[I,J];
Pr:=Pr*A[I,J];
end;
WriteLn('s=',S:8:2, ' pr=',Pr:8:2);
end;
Приведенный фрагмент программы позволит вычислить сумму и произведение элементов каждой строки матрицы, а не всех элементов матрицы.
При вычислении максимального и минимального элементов матрицы также надо правильно устанавливать начальные значения вычисляемых переменных, а также правильно задавать пределы изменения параметров циклов:
Amax:=A[1,1]; Imax:=1; Jmax:=1;
Amin:=A[1,1]; Imin:=1; Jmin:=1;
for I:=1 to M do
for J:=1 to N do
if A[I,J]>Amax then
begin
Amax:=A[I,J];
Imax:=I;
Jmax:=J;
end
else if A[I,J]<Amin then
begin
Amin:=A[I,J];
Imin:=I;
Jmin:=J;
end;
WriteLn('amax=',Amax:8:2, ' imax=',Imax:2
,' jmax=',Jmax:2, ' amin=',Amin:8:2
,' imin=',Imin:2, ' jmin=',Jmin:2,);
В приведенном фрагменте программы нельзя опускать операторы присваивания начальных значений индексам минимального и максимального элементов (Imax:=1; Jmax:=1;Imin:=1; Jmin:=1;). В случае отсутствия указанных операторов индексы искомых элементов будут не определены в том случае, если первый элемент A[1,1] является максимальным (минимальным).
При поиске минимального (максимального) элемента матрицы нельзя устанавливать начальное значение параметра цикла, равное двум, как это можно сделать при обработке одномерного массива. Следующий фрагмент программы будет приводить к неверному результату, так как будут исключены из рассмотрения все элементы первой строки, за исключением первого, значение которого выбирается в качестве начального значения для максимума и минимума.
max:=A[1,1]; Imax:=1; Jmax:=1;
min:=A[1,1]; Imin:=1; Jmin:=1;
for I:=2 to M do
for J:=1 to N do
.....................
Рассмотрим примеры обработки матриц.
