Вероятностно-статистические аспекты метода Монте-Карло и имитационного моделирования
Как уже отмечалось выше, при решении задач методом МК или ИМ следует иметь в виду, что получаемые результаты являются фактически исходами вычислительного эксперимента. Следовательно, эти результаты должны интерпретироваться с точки зрения математической статистики. В соответствии с законом больших чисел, свойства устойчивости результаты приобретают после многократного повторения такого эксперимента. Вопрос о достаточности числа вычислительных опытов может ставиться только для конкретной системы и при известных начальных условиях. Рассмотрим пример определения площади круга из главы 1 данной работы. Выберем число наблюдений (в ИМ это число чаще называют числом прогонов модели)
N=10. Меняя продолжительность прогона от 100 до 10000 точек, вычислим средние выборочные и дисперсии для каждого из этих случаев. Для наглядности приведем программу вычислений площади круга еще раз. Результаты сведем в таблицу.
| Точное значение площади круга |
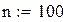 |
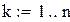 |
| Длина прогона |
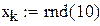 |
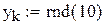 |
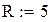 |
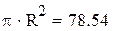 |
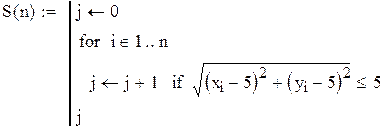 |
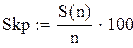 |
 |
| Результат единичного опыта |
| Номер опыта | Оценка площади круга при фиксированном числе n | ||||||
| n=100 | n=200 | n=500 | n=1000 | n=2000 | n=5000 | n=10000 | |
| 77.5 81.5 74.5 77.5 79.5 78.5 76.5 | 77.8 74.2 79.2 80.4 78.6 81.4 76.2 78.6 79.2 | 77.4 78.3 75.6 78.9 78.8 78.0 77.9 76.5 79.5 78.1 | 77.15 78.95 79.85 79.0 77.6 78.5 79.1 79.75 77.6 78.5 | 78.84 78.92 78.56 77.98 78.54 78.26 79.24 78.28 79.44 78.78 | 78.66 77.97 78.9 78.62 79.19 78.0 77.82 78.66 78.32 78.58 | ||
| Среднее | 75.8 | 77.35 | 78.06 | 77.9 | 78.6 | 78.68 | 78.46 |
| Дисперсия | 15.76 | 5.15 | 4.76 | 1.21 | 0.75 | 0.18 | 0.17 |
По данным расчетов, приведенных в таблице можно сделать следующие выводы.
1. С ростом числа генерируемых точек (продолжительности прогона модели) оценки площади круга приближаются к точному значению.
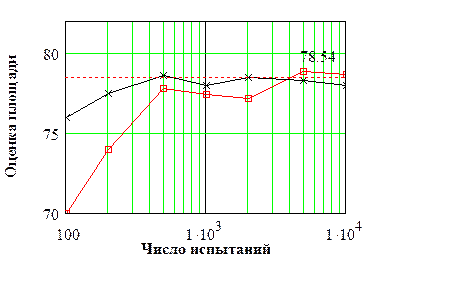
На графике показаны оценки площади круга для прогонов 1 и 6 в зависимости от продолжительности прогона. Видно, что сначала оценки испытывают сильные колебания, а затем стабилизируются вблизи точного значения. Наблюдаемое явление типично для любой имитационной модели.
2. Прогоны модели, отличающиеся друг от друга только последовательностями случайных чисел, дают различные оценки при одном и том же значении n.
3. Отметим, что влияние переходных условий уменьшается при усреднении результатов прогонов (это хорошо видно из строки таблицы для средних выборочных).
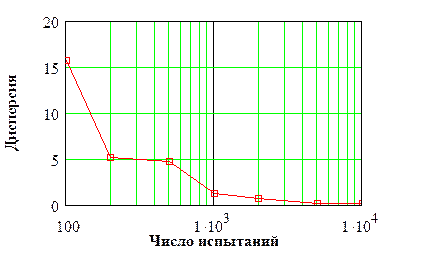
4. Дисперсия рассматриваемой случайной величины существенно уменьшается при увеличении продолжительности прогона с 100 до 200, а затем ее уменьшение незначительно. Этот факт так же характерен для имитационных моделей, что позволяет подобрать оптимальное для рассматриваемей задачи значение n, по критерию точность− затраты машинного времени.
5. Наряду с точечными оценками, рассмотрим доверительные интервалы, показывающие величины отклонений от точных значений. Пусть 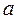 представляет собой точное значение, а
представляет собой точное значение, а 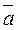 и
и 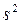 − среднее и дисперсию в
− среднее и дисперсию в 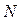 наблюдениях, тогда при доверительной вероятности
наблюдениях, тогда при доверительной вероятности 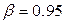 вычислим доверительный интервал как
вычислим доверительный интервал как 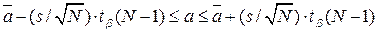 , где
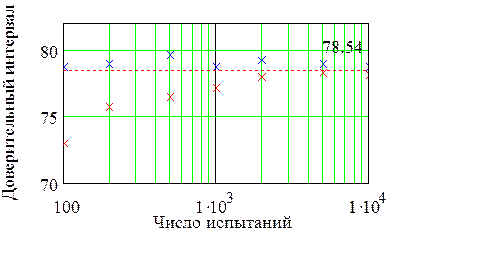
, где 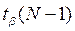 обозначает квантиль распределения Стьюдента с
обозначает квантиль распределения Стьюдента с 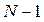 степенями свободы. Результаты, приведенные на графике, показывают, что все доверительные интервалы содержат точное значение площади и становятся меньше с ростом продолжительности прогона. Этот факт характерен для имитационных моделей и должен учитываться в дополнение к известному выводу математической статистики − уменьшение доверительного интервала с ростом числа наблюдений.
степенями свободы. Результаты, приведенные на графике, показывают, что все доверительные интервалы содержат точное значение площади и становятся меньше с ростом продолжительности прогона. Этот факт характерен для имитационных моделей и должен учитываться в дополнение к известному выводу математической статистики − уменьшение доверительного интервала с ростом числа наблюдений.
Другим широко используемым способом понижения дисперсии является так называемый антитетический метод. В основе метода лежит очевидный факт, что если 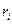 случайное число, равномерно распределенное на интервале (0,1), то и
случайное число, равномерно распределенное на интервале (0,1), то и 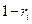 обладает теми же свойствами. В соответствии с методом проводится два прогона модели с указанными случайными числами и находится их среднее арифметическое. Далее поступают указанным выше способом.
обладает теми же свойствами. В соответствии с методом проводится два прогона модели с указанными случайными числами и находится их среднее арифметическое. Далее поступают указанным выше способом.
Приведенное здесь обсуждение показывает, что имитационное моделирование не сводится к разработке модели и составлению машинной программы, а представляет собой статистический эксперимент и его результаты необходимо рассматривать именно с этой точки зрения.
Задание по разделу: студент выбирает определенный интеграл (любой берущийся в элементарных функциях), находит его точное значение и проводит статистический анализ результатов по схеме приведенной выше. Результаты представляются в виде таблицы и графиков.
4. Моделирование Марковских процессов.
4.1 Марковская цепь с дискретным временем.
Рассмотрим, для простоты, Марковскую цепь с тремя состояниями (k=3). (Подробное изложение теории Марковских цепей см. [4,5]). Переходы между состояниями происходят мгновенно в фиксированные моменты времени. Вероятности переходов из любого состояния Si в любое другое Sj считаются заданными и равны pij. Моделирование системы требует симуляции стохастических воздействий на систему (случайных чисел и случайных событий ). Получение СЧ описано в главе 3, а случайные события, образующие полную группу, с заданными вероятностями можно моделировать следующим образом. Пусть событие А имеет вероятность р(А), а противоположное событие 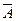 − (1-р(А)) . Разыграем одну реализацию случайной величины имеющей равномерное распределение на интервале
− (1-р(А)) . Разыграем одну реализацию случайной величины имеющей равномерное распределение на интервале 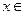 (0,1). Если
(0,1). Если 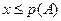 , то полагают, что произошло событие А, если
, то полагают, что произошло событие А, если 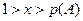 , то произошло противоположное событие. Приведем пример с большим числом событий. Пусть события А,В,С образуют полную группу и попарно несовместны, и р(А)=0.3, В – р(В)=0.5 и С– р(С)=0.2. Тогда, если полученное случайное число х меньше 0.3, то полагают, что произошло событие А , если х меньше 0.8, но больше 0.3 – событие В и при х больше 0.8 – событие С. При многократном повторении элементарных опытов по определения вероятности событий по приведенной схеме частота появления каждого события будет стремиться к его вероятности.
, то произошло противоположное событие. Приведем пример с большим числом событий. Пусть события А,В,С образуют полную группу и попарно несовместны, и р(А)=0.3, В – р(В)=0.5 и С– р(С)=0.2. Тогда, если полученное случайное число х меньше 0.3, то полагают, что произошло событие А , если х меньше 0.8, но больше 0.3 – событие В и при х больше 0.8 – событие С. При многократном повторении элементарных опытов по определения вероятности событий по приведенной схеме частота появления каждого события будет стремиться к его вероятности.
Поставим конкретную задачу. Для Марковской цепи с тремя состояниями задана матрица вероятностей переходов за один шаг Р.
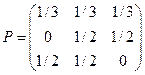
1. Составить размеченный граф состояний этой Марковской цепи, определить, является ли цепь регулярной.
2. Найти стационарное распределение вероятностей состояний.
3. Выполнить моделирование системы и сравнить полученные результаты с результатами, полученными ранее в пункте 2.
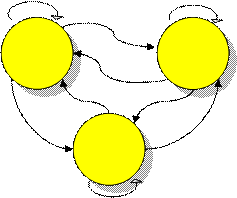
Решение. 1. Составим граф состояний.
 1/3 0
1/3 0
|
|
1/2
1/3 0
1/2 1/2
|
1/2
По графу видно, что все состояния системы существенны, поэтому цепь регулярна и обладает финальными вероятностями состояний.
2. По формулам, [5] 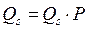 найдем стационарное распределение вероятностей. Запишем систему алгебраических уравнений соответствующую данному матричному
найдем стационарное распределение вероятностей. Запишем систему алгебраических уравнений соответствующую данному матричному
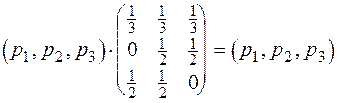
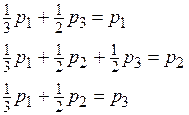 Þ
Þ 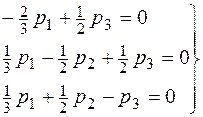 .
.
Система имеет бесчисленное множество решений, причем одно из уравнений является следствием двух других. Чтобы найти единственное решение, отбросим лишнее уравнение и добавим условие нормировки 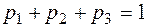 .
.
Решим систему уравнений:
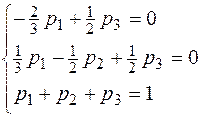 Þ
Þ 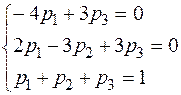 ,
,
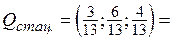 (0,231; 0,461; 0,308).
(0,231; 0,461; 0,308).
3. Моделирование процесса, протекающего в данной системе.
Примем, что в начальный момент времени система находится в состоянии S0 и Q(0) = (1, 0, 0). Пусть число шагов моделирования или продолжительность прогона равна ns. Введем матрицу В − индикатор состояния, (например, столбец 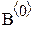 показывает, что система после последнего шага находится в состоянии S0) и вектор so для суммирования числа попаданий в каждое из состояний. Так как в начальный момент времени система находилась в состоянии
показывает, что система после последнего шага находится в состоянии S0) и вектор so для суммирования числа попаданий в каждое из состояний. Так как в начальный момент времени система находилась в состоянии 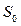 , то
, то 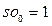 , а
, а 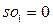 и
и 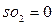 .
. 
Основные обозначения, используемые в приведенной ниже программе.
jm− счетчик числа шагов, x − случайные числа, равномерно распределенные на интервале (0,1). Значение индекса k определяет номер состояния, из которого выходит система, а номер состояния, в которое осуществляется переход, получим из соотношений переходных вероятностей. Вектор sо, элементы которого есть числа попаданий системы в данное состояние. Элементы этого вектора будут возрастать на 1, как только система попадает в это состояние. Формальными параметрами программы являются число шагов N и вектор s.
Краткое описание работы программы.
Счетчику jm присваивается начальное значение 0, выбирается столбец 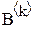 соответствующий начальному состоянию и строится цикл while до достижения значения N счетчика jm. Внутри цикла определяется значение индекса k или номера состояния, из которого будет проходить переход, затем, в соответствии со значениями переходных вероятностей, находится состояние i , в которое перейдет система. В рассматриваемом примере, вероятности переходов из состояния
соответствующий начальному состоянию и строится цикл while до достижения значения N счетчика jm. Внутри цикла определяется значение индекса k или номера состояния, из которого будет проходить переход, затем, в соответствии со значениями переходных вероятностей, находится состояние i , в которое перейдет система. В рассматриваемом примере, вероятности переходов из состояния 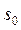 в
в 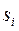 равны
равны 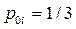 . Тогда, если следующее случайное число х меньше или равно 1/3, то произойдет событие
. Тогда, если следующее случайное число х меньше или равно 1/3, то произойдет событие 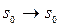 , если
, если 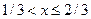 , то
, то 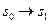 и при
и при 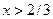
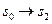 , и число
, и число 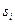 возрастет на единицу. Индикатор состояний приводится в положение соответствующее совершенному переходу. К счетчику шагов прибавляется единица. Далее расчет продолжается аналогично. Результатом моделирования будут компоненты вектора s − числа попаданий в каждое из состояний.
возрастет на единицу. Индикатор состояний приводится в положение соответствующее совершенному переходу. К счетчику шагов прибавляется единица. Далее расчет продолжается аналогично. Результатом моделирования будут компоненты вектора s − числа попаданий в каждое из состояний.
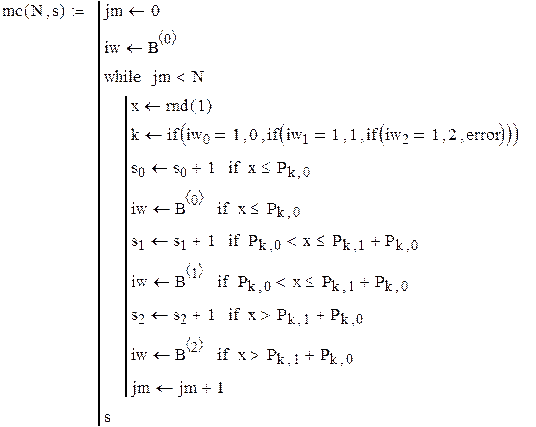
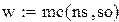 |
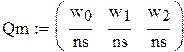 |
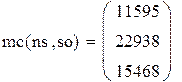
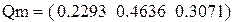 |
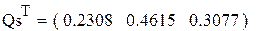 |
Сравнивая результаты моделирования при различных прогонах с различными числами шагов и точные значения стационарных вероятностей состояний, делаем вывод о хорошей сходимости результатов моделирования к точным значениям при N > 10000 шагов.
