Пример изображения графика функции sin
Программа содержит массив из 1000 структур POINT. В цикле от 0 до 999 член x структуры растет от 0 до cxClient. В каждом цикле член структуры определяет значение синуса и масштабируется до размеров клиентской области окна. Вся кривая целиком отображается с использованием одного вызова функции Polyline (рис. П 6.3).
Текст программы может быть следующим:
#include <windows.h>
#include <math.h>
#define NUM 1000
#define TWOPI (2 * 3.14159)
LRESULT CALLBACK WndProc (HWND, UINT, WPARAM, LPARAM) ;
int WINAPI WinMain (HINSTANCE hInstance, HINSTANCE hPrevInstance,
PSTR szCmdLine, int iCmdShow)
{
static char szAppName[] = "Sin" ;
HWND hwnd ;
MSG msg ;
WNDCLASSEX wndclass ;
wndclass.cbSize = sizeof (wndclass) ;
wndclass.style = CS_HREDRAW | CS_VREDRAW ;
wndclass.lpfnWndProc = WndProc ;
wndclass.cbClsExtra = 0 ;
wndclass.cbWndExtra = 0 ;
wndclass.hInstance = hInstance ;
wndclass.hIcon = LoadIcon (NULL, IDI_APPLICATION) ;
wndclass.hCursor = LoadCursor (NULL, IDC_ARROW) ;
wndclass.hbrBackground=(HBRUSH) GetStockObject(WHITE_BRUSH);
wndclass.lpszMenuName = NULL ;
wndclass.lpszClassName = szAppName ;
wndclass.hIconSm = LoadIcon (NULL, IDI_APPLICATION) ;
RegisterClassEx (&wndclass) ;
hwnd = CreateWindow (szAppName, "Second Example",
WS_OVERLAPPEDWINDOW,
CW_USEDEFAULT, CW_USEDEFAULT,
CW_USEDEFAULT, CW_USEDEFAULT,
NULL, NULL, hInstance, NULL) ;
ShowWindow (hwnd, iCmdShow) ;
UpdateWindow (hwnd) ;
while (GetMessage (&msg, NULL, 0, 0)) {
TranslateMessage (&msg) ;
DispatchMessage (&msg) ;
}
return msg.wParam ;
}
LRESULT CALLBACK WndProc (HWND hwnd, UINT iMsg,
WPARAM wParam, LPARAM lParam)
{
static int cxClient, cyClient ;
HDC hdc ;
int i ;
PAINTSTRUCT ps ;
POINT pt [NUM] ;
switch (iMsg) {
case WM_SIZE:
cxClient = LOWORD (lParam) ;
cyClient = HIWORD (lParam) ;
return 0 ;
case WM_PAINT:
hdc = BeginPaint (hwnd, &ps) ;
MoveToEx (hdc, 0, cyClient / 2, NULL) ;
LineTo (hdc, cxClient, cyClient / 2) ;
for (i = 0 ; i < NUM ; i++) {
pt[i].x = i * cxClient / NUM ;
pt[i].y = (int) (cyClient / 2 * (1 - sin (TWOPI * i / NUM))) ;
}
Polyline (hdc, pt, NUM) ;
return 0 ;
case WM_DESTROY:
PostQuitMessage (0) ;
return 0 ;
}
return DefWindowProc (hwnd, iMsg, wParam, lParam) ;
}
Результат работы программы:
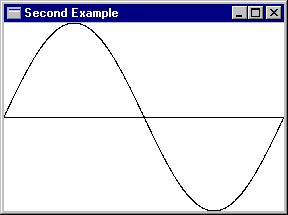
Рис. П 6.3
Рисование замкнутых фигур
Рассмотрим функции для рисования замкнутых фигур:
Rectangle – прямоугольник; Ellipse – эллипс; RoundRect – прямоугольник со скругленными углами; Chord – дуга кривой эллипса, концы которой соединены хордой; Pie – кусок, вырезанный из эллипса; Polygon – многоугольник; PolyPolygon – множество многоугольников.
Контур фигуры рисуется текущим пером, а фигура закрашивается текущей кистью. По умолчанию это стандартная кисть WHITE_BRUSH.
Простейшей является функция рисования прямоугольника:
Rectangle (hdc, x1, y1, x2, y2);
(x1, y1) – координаты левого верхнего угла, (x2, y2) – правого нижнего угла.
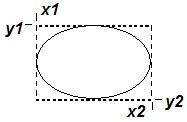 Для рисования эллипса используется функция, имеющая те же параметры:
Для рисования эллипса используется функция, имеющая те же параметры:
Ellipse (hdc, x1, y1, x2, y2);
Фигура, отображаемая функцией Ellipse (вместе с ограничивающим прямоугольником).
Функция для рисования прямоугольника со скругленными углами:
RoundRect (hdc, x1, y1, x2, y2, xEllipse, yEllipse);
имеет два дополнительных параметра: для рисования скругленных углов используется маленький эллипс, шириной xEllipse, высотой yEllipse. Фигура, отображаемая этой функцией, приведена на рисунке. Скругленные углы были нарисованы с использованием размеров эллипса, вычисленных по формулам
xEllipse = (x2–x1)/4; yEllipse = (y2–y1)/4;
Это простое приближение, но результаты скорее всего будут выглядеть не совсем правильно, потому что округлость углов более заметна при больших размерах прямоугольника.
Функции Chord (сегмент эллипса) и Pie (сектор эллипса) имеют одинаковые параметры:
Chord (hdc, x1, y1, x2, y2, xStart, yStart, xEnd, yEnd);
Pie (hdc, x1, y1, x2, y2, xStart, yStart, xEnd, yEnd);
При рисовании используется воображаемая линия для соединения точки (xStart, yStart – начало дуги) с центром эллипса. В точке, где эта линия пересекается с ограничивающим прямоугольником, начинается рисование дуги эллипса в направлении против часовой стрелки; аналогично используется воображаемая линия для соединения точки (xEnd, yEnd – конец дуги) с центром эллипса. В точке, где эта линия пересекается с ограничивающим прямоугольником, завершается рисование дуги.
В функции Chord соединяются конечные точки дуги, а в функции Pie соединяются начальная и конечная точки дуги с центром эллипса.
Фигуры, отображаемые функциями Chord и Pie, приведены на рис. П 6.3.
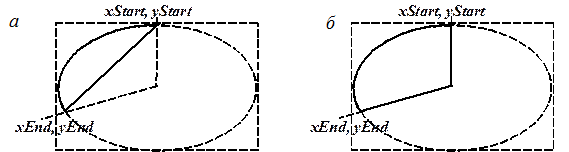
Рис. П 6.3. Фигуры, нарисованные с использованием:
а – функции Chord; б – функции Pie
