Анализ эффективности быстрой сортировки
В среднем число операций порядка N×log2N, остальные сортировки в среднем N2 операций.
Преимущество быстрой сортировки проявляется при больших N. Она сортирует массив с элементами в обратном порядке практически с такой же скоростью, как уже отсортированный массив.
Принцип быстрой сортировки
Причина неэффективности метода сортировки обменом (метод «пузырька») в том, что меняются местами два соседних элемента, если для них нарушена упорядоченность. Менять местами надо максимально удаленные элементы.
Алгоритм одного шага быстрой сортировки
| 1) Положить i=1, j=N 2) Выбрать в массиве случайным образом элемент x. 3) Повторять Просматривая массив слева направо, найти элемент Ai>x. Просматривая массив справа налево, найти элемент Aj<x. Если i<=j, то поменять местами Ai и Aj, увеличить i+1, уменьшить j-1 | Пример одного шага быстрой сортировки 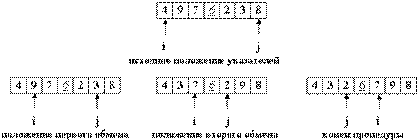 |
Для сортировки массива надо то же самое проделать с обеими частями (слева и справа от x), затем с частями этих частей и т.д. до тех пор, пока каждая часть не будет содержать только один элемент. Получили рекурсивный алгоритм.
procedure QSort(L,R:integer);//L, R – индексы самого левого и самого правого элементов подмассива
var i,j,x,w:integer;
begin
i:=L; j:=R;
x:=A[(L+R) div 2]; //x - средний элемент
repeat
while A[i]<x do i:=i+1; //Просмотр слева направо
while A[j]<x do j:=j-1; //Просмотр справа налево
if i<=j then
begin //Перестановка A[i] и A[j]
w:=A[i];
A[i]:=A[j];
A[j]:=w;
i:=i+1; j:=j-1
end
until i>j;
if L<j then QSort(L,j); //Рекурсивный вызов для левой половины массива
if i < R then QSort(i,R) //Рекурсивный вызов для правой половины массива
End;
begin… Sort(1,N); . . .
End.
Задача о Ханойских башнях
Имеется башня из n дисков различного диаметра, нанизанных на один из трех стержней. Требуется построить аналогичную башню на другом стержне с использованием третьего при выполнении двух условий:
- перемещать можно только один диск;
- на диске меньшего диаметра нельзя помещать диск большего диаметра.
Трудолюбивые буддийские монахи день и ночь переносят диски со стержня на стержень. Легенда утверждает, что когда монахи закончат свою работу, наступит конец света. Для решения задачи с 64 дисками потребуется (264 – 1) перемещений. Поэтому конец света по легенде произойдет по истечении более 5 миллиардов веков, если считать, что один диск перемещается за одну секунду. Задачу и легенду для неё придумал в 1883 г. французский математик Э. Люка.
| program Towers; {Перемещение с А на С, В - промежуточный} var N : integer; {число дисков} procedure Move(n:byte; A, C, B : char); begin if n=1 then writeln(A,’->’, C) else begin Move(n-1, A, B, C); writeln(A,’->’, C); Move(n-1, B, C, A) end end; begin write(’Число дисков=’); readln(N); Move(N, ’A’, ’C’, ’B’) end. | 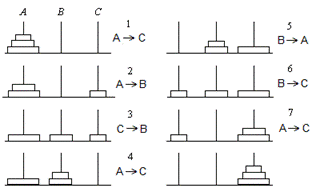 |
Указатели
Указательные типы
| Указателем называется переменная указательного типа, в которой хранится адрес некоторого объекта (например, переменной). Говорят, что указатель указывает или ссылается на другую переменную. | 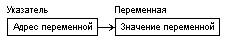 |
Указатель занимает в памяти 4 байта.
Нулевой указатель – это указатель, который не ссылается ни на какой объект.
Для его обозначения служит константа Nil.
В языке Pascal различают два вида указателей:
1) бестиповые указатели, которые могут содержать адреса переменных любого типа. Они объявляются через стандартный указательный тип pointer, например: var p:pointer;
2) типизированные указатели, которые могут указывать на переменные только определенного типа; этот тип называется базовым типом для этих указателей. Далее будем рассматривать только типизированные указатели.
