Поперечные размеры и расстояния

Если измеряемые размеры составляют несколько миллиметров, то исследуемое распределение интенсивностей проецируют на круглый экран со шкалами модуля 5. Если же характерные размеры составляю доли миллиметра, то используют микропроектор.

Исследуемое распределение, например, дифракционную картину или измеряемый объект размещают в объектной плоскости линзы модуля 3. Увеличенное изображение наблюдают на экране фотоприемника и измеряют размер Н изображения. Размер объекта

(2)

где - коэффициент увеличения микропроектора.

Для измерения расстояния между удаленными объектами нужно получить их изображения в объектной плоскости микропроектора, определить согласно (2) расстояние между изображениями, затем вычислить . Изображение можно получить с помощью объектива (модуль 6) или собирающей линзы из набора объектов.

Распределение интенсивности

Изучаемое распределение интенсивности или изображение объекта размещают и нужным образом ориентируют в окне фотоприёмника. Для перемещения изображения используют юстировочные винты двухкоординатных держателей оптических элементов. Для изменения ориентации изображения используют возможность поворота обоймы двухкоординатного держателя на произвольный угол.

Для измерения распределения интенсивности изображение смещают, поворачивая барабан модуля 3 на угол, соответствующий выбранному интервалу измерений, и снимают отсчеты напряжения после каждого смещения. Одновременно снимают отсчет координаты соответствующей точки объекта по шкалам микропроектора.

Значения интенсивности в условных единицах (милливольтах) показываются цифровым вольтметром. Для нахождения интенсивности в абсолютных единицах необходима калибровка фоторегистратора. В большинстве экспериментов важны лишь относительные значения интенсивности. Тогда калибровка не требуется, и используются условные значения интенсивности в милливольтах.

Внимание!

Мощность излучения лазера плавно нарастает в течение 10-15 минут после включения. После прогрева остаются колебания мощности с периодом 1÷10 секунд и с размахом порядка 10% средней мощности. Воспроизвдимость результатов повышается, если брать отсчеты, соответствующие максимумам показаний фотоприемника.

2. В лазерах с неполяризованным излучением наблюдаются еще и хаотические изменения поляризации. Это приводит к сильным колебаниям интенсивности в опытах с поляризованным светом- (темы 28 и 30), что затрудняет интерпретацию результатов. Однако если брать соответствующие максимумам показаний фотоприемника результаты получаются вполне удовлетворительными.

3. Если источник излучения - лампа накаливания, то поляризаторы и светофильтры при визуальном наблюдении ведут себя как положено, а при фотометрических измерениях практически не работают. Дело в том, что основная часть мощности излучения лампы приходится на инфракрасный диапазон. В этом же диапазоне (до 2мкм) наиболее чувствителен фотоприёмник, а поляризаторы и светофильтры построены для излучения видимого диапазона. Из набора фильтров модуля 28 только зелёный светофильтр заметно задерживает инфракрасное излучение, остальные его пропускают. Для фотометрических опытов с белым светом нужно предварительно разложить его в спектр или отсечь инфракрасную составляющую. В ЛКО-IА это не предусмотрено, и опыты с фотометрией проводятся с использованием лазера.

Приложение 6.

Функция Бесселя.

Функции Бесселя в математике, это семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:

где 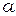- произвольное действительное число, называемое порядком.

Наиболее часто используемые функции Бесселя - функции целых порядков.

Хотя 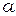и (- 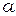) порождают одинаковые уравнения, обычно договариваются о том, чтобы им соответствовали разные функции (это делается, например, для того, чтобы функция Бесселя была гладкой по ).

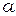Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.

Уравнение Бесселя возникает во время нахождения решений Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например:

• электромагнитные волны в цилиндрическом волноводе;
• теплопроводности в цилиндрических объектах;
• формы колебания тонкой круглой мембраны
• распределение интенсивности света, дифрагированного на круглом отверстии.
• скорость частиц в цилиндре, заполненном жидкостью и вращающемся вокруг своей оси.

Функции Бесселя применяются и в решении других задач, например, при обработке сигналов.

Функциями Бесселя первого рода, обозначаемыми , являются решения, конечные в точке x = 0 при целых или неотрицательных 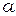. Выбор конкретной функции и её нормализации определяются её свойствами. Можно определить эти функции с помощью разложения в ряд Тейлора около нуля (или в более общий степенной ряд при нецелых ):

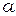Здесь - это гамма-функция Эйлера, обобщение факториалф на нецелые значения. График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально , хотя на самом деле нули функции расположены не периодично.

Ниже приведены графики для 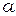= 0,1,2:

Позиция № 251

в плане издания

учебной литературы

МГУ на 2010 г.

Учебное издание

Юрий Дмитриевич Воробьёв

Волновая оптика Дифракция

Учебное пособие

Печатается в авторской редакции

9,3 уч.-изд. л. Формат 60 ´ 84 1/16

Тираж 30 экз. Заказ №

Отпечатано в типографии РПК МГУ им. адм. Г. И. Невельского

690059, Владивосток, ул. Верхнепортовая, 50а