Решения нелинейных уравнений.
Многие уравнения, например трансцендентные, не имеют аналитических решений. Однако они могут решаться численными методами с заданной погрешностью. Для простейших уравнений вида F(x)=0 решение находится с помощью функции root(Выражение, Имя переменной). Эта функция возвращает значение переменной с указанным уровнем, при котором выражение дает 0.Функция реализует вычисления итерационным методом, причем можно задать начальное значение переменной. Это особенно полезно, если возможно несколько решений.
Пример: Вычисление корней кубического полинома. Кубическое уравнение обязательно имеет хотя бы один кубический корень x1. Он определяется с помощью функции root.
Порядок выполнения:
1. Ввод коэффициентов полинома.
2. Ввод полинома.
3. Вычисление действительного корня с помощью функции root.
4. Вычисление двух других корней.
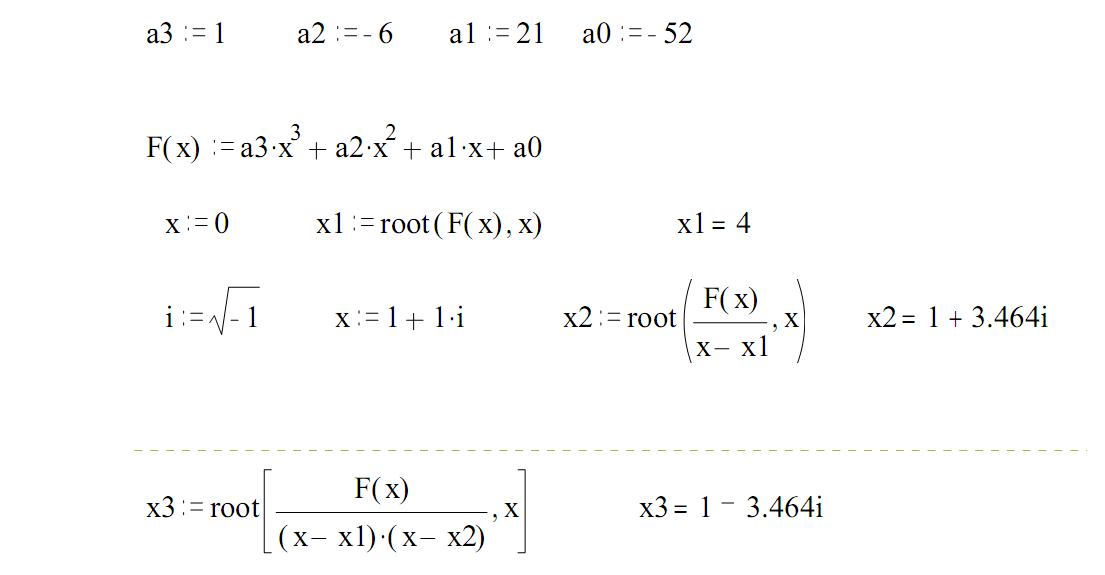 Задание к работе:
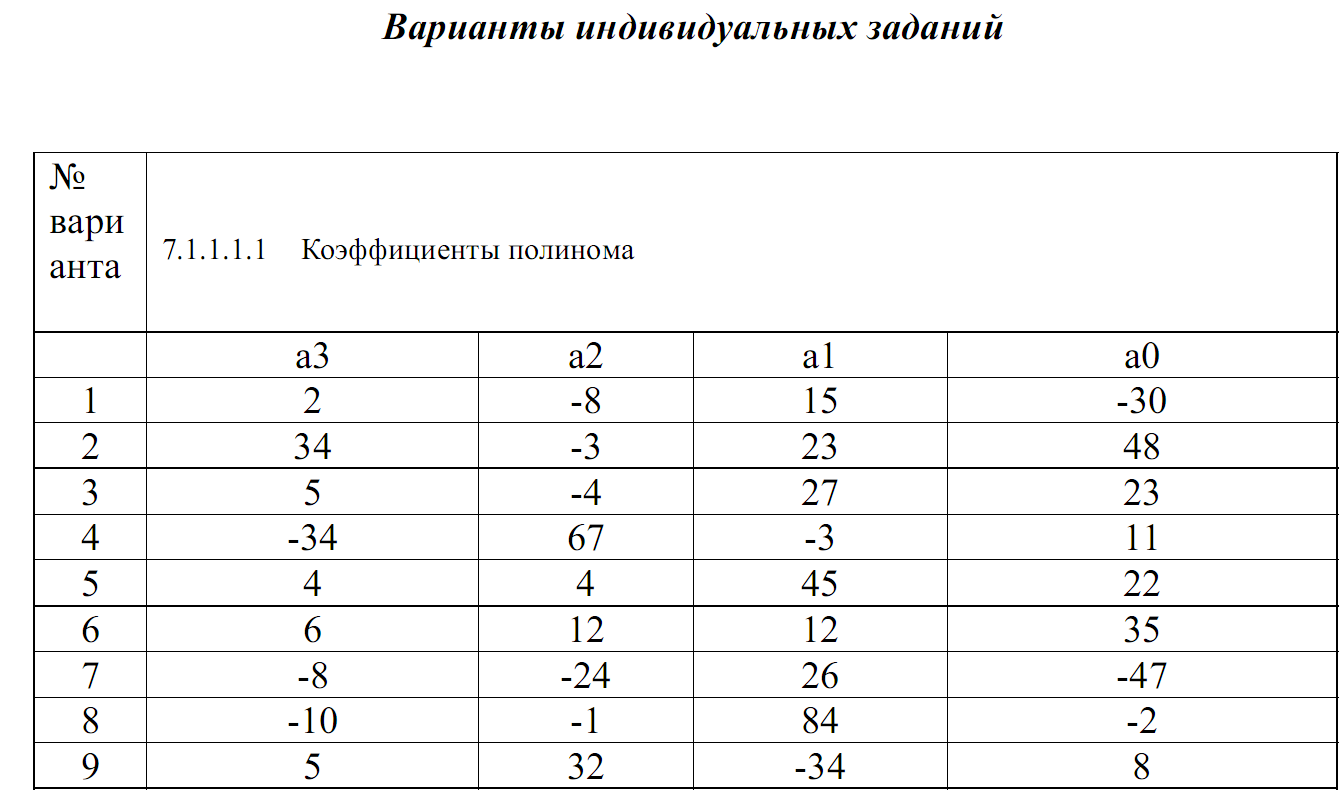
Задание к работе:
Вычислить корни кубического полинома и построить график.
F(x)=a3*x3+a2*x2+a1*x+a0
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |

Литература:
1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича.
2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб. : БХВ-Петербург, 2006. -336 с. : ил.
3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000.
4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с.
5. Ушаков А. Н. , Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| Разраб. |
| Провер. |
| Скачкова Л.П. |
| Реценз. |
| Н. Контр. |
| Утверд. |
| Лит. |
| Листов |
| КФ ГОУ ОГУ |
«Решение уравнений и систем»
Цель работы: С помощью средств MathCAD научиться находить графическое, аналитическое, численное решения уравнений. Исследовать на разрешимость системы уравнений.
Рекомендуемая литература:[1–5, 10].
Задание:
1. Найти все корни уравнения n-й степени: графически, численно и аналитически.
2. Сделать проверку полученного решения.
3. Найти численное и графическое решение трансцендентного уравнения.
4. Сделать проверку полученного решения.
5. Исследовать систему уравнений на разрешимость. Построить график.
6. Решить систему уравнений.
7. Сделать проверку полученного решения.
Пример выполнения задания:
Задание:
| Уравнение n-й степени | Трансцендентное уравнение |
| 6x3-25x2-11x+60=0 | e2x+cos(3x) |
| Матрица системы | Вектор правой части |
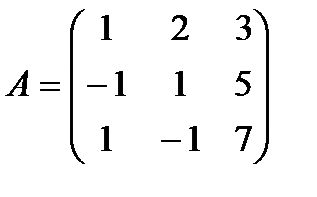 | 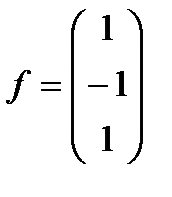 |
1. Найдем решение кубического уравнения. Для этого запишем его коэффициенты в следующем виде:

Определим полином

Найдем решение уравнения y(x)=0 графически. Для этого построим график, как это было описано в лабораторной работе № 2, но не указывая границы по оси Y (эти границы MathCAD проставляет сам). В результате получаем:
 |
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Получим корни уравнения y(x)=0 аналитически. Для этого в MathCAD предназначена функция solve на панели инструментов «Символы». Имеем:

Можно убедиться, что наша оценка корней по графику была верной.
Для нахождения корней уравнений n-й степени имеется специальная функция polyroots, в качестве параметра которой задается вектор коэффициентов:

В MathCAD имеется функция root, которая позволяет находить корень из заданного интервала для любых уравнений. В частности, для уравнений n-й степени имеется два способа использования этой функции.
Примечание. В данной функции реализован метод Ньютона для нахождения корней уравнения, поэтому необходимо задавать начальное значение x, с которого и начинается поиск корня.
Первый способ. Задаем начальное значение x:

Вызываем функцию:

где y(x) – заданная левая часть уравнения y(x)=0; x – приближенное значение аргумента; (–2) – левый край интервала, которому принадлежит искомый корень; (–1) – правый край интервала.
Для просмотра полученного значения достаточно набрать «X11=», получим:

Оставшиеся два корня ищутся аналогично:

В результате получим:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |

Второй способ. Задаем начальное значение x := -1
и вызываем функцию:

Здесь интервалы не указываем, и функция ищет ближайший к заданному значению корень:

Для нахождения второго корня задаем значение x := 1
и исключаем из функции уже найденный корень:

Получили значение:

Третий корень ищем по аналогии:

2. Выполним проверку полученного решения:


Мы видим, что корень из интервала [1; 2] более точно найден функцией solve.
3. Трансцендентные уравнения можно решать графически, разбив уравнения на два более простых. Например, наше уравнение, заданное в виде

разобьем на два:

Построим графики этих уравнений:
 |
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |



4. Выполним проверку полученного решения:

Можно увидеть, что корни находятся с достаточно хорошей точностью, но с удалением от точки 0 точность начинает ухудшаться.
5. Зададим систему уравнений матрицейА и вектором правых частей f:

Проведем исследование данной системы на разрешимость, для этого вычислим определитель матрицыА:

Определитель матрицы не равен нулю, следовательно, наша система разрешима и имеет единственное решение.
Получим данное решение графически. Для этого построим каждую плоскость отдельно. В MathCAD плоскости задаются так:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |

Графическое представление этих плоскостей имеет вид:

| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
6. Решим систему уравнений матричным методом. Для этого найдем обратную матрицу:  .
.
Теперь можно найти решение системы:  .
.
Вектор неизвестных имеет вид:

7. Сделаем проверку:

Литература:
1. Информатика: Базовый курс. Учебник под редакцией С.В.Симановича.
2. Половко А.М., Ганичев И.В. MathCad для студента. – Спб. : БХВ-Петербург, 2006. -336 с. : ил.
3. Ю.Ю.Тарасевич Численные методы на MathCad. – Астраханский гос. Пед. Ун-т: Астрахань,2000.
4. Могилёв, А. В., и др. Информатика: Учеб. Пособие Под. Ред. Хеннера Е. К. М.: Изд. Центр “Академия”,2000. -816с.
5. Ушаков А. Н. , Ушакова Н. Ю. Секреты для инженерных и научных расчетов. – Оренбург: ОГУ, 2001. - №--с.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
