Дифракционные задачи с сетевой симметрией

ДИСЦИПЛИНА

«ЭЛЕКТРОННЫЕ УСТРОЙСТВА ОТБРАЖЕНИЯ ИНФОРМАЦИИ»

ЛАБОРАТОРНАЯ РАБОТА №2.

Пространственные процессы при дифракции Френеля и Фраунгофера.

Цель работы

Цель работы: на примере различных входных отверстий рассмотреть распределение интенсивности в пространстве и получить дифракции Френеля и Фраунгофера.

Предварительное задание.

1. Зона Фраунгофера и зона Френеля. Что это?

2. Дифракция Френеля. Спираль Корню. Что она показывает?

3. Дифракция Фраунгофера. Дифракция на круглом отверстии. Что представляет из себя дифракционная картина?

4. Дифракция Фраунгофера. Дифракция на щелевом отверстии. Что представляет из себя дифракционная картина?

Методические указания к выполнению работы.

Дифракция света

Принцип Гюйгенса-Френеля

Дифракцией света принято называть отклонение от прямолинейного распространения света вблизи препятствий, например, при прохождении света через отверстие. Строгое решение дифракционных задач может быть, в принципе, найдено, исходя из волнового уравнения и граничных условий. Однако, в такой строгой постановке решение, ввиду сложности, удается получить только в нескольких простейших случаях. В оптике, как правило, используются приближенные методы, опирающиеся на принцип Гюйгенса-Френеля. Получаемые при этом решения вполне пригодны для практических приложений.

Принцип Гюйгенса-Френеля следует рассматривать как рецепт приближенного решения дифракционных задач. В основе его лежит допущение о том, что каждый элемент поверхности волнового фронта можно рассматривать как источник вторичных волн, распространяющихся во всех направлениях (рис. 1.). Эти волны когерентны, так как они возбуждены одной и той же первичной волной. Результирующее поле в точке наблюдения P может быть найдено как результат интерференции вторичных волн. В качестве поверхности вторичных источников может быть выбрана не только поверхность волнового фронта, но и любая другая замкнутая поверхность. При этом фазы и амплитуды вторичных волн определяются значениями фазы и амплитуды первичной волны.

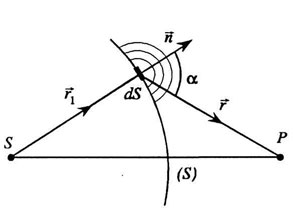Рис.1. Принцип Гюйгенса–Френеля.

При решении дифракционных задач, когда речь идет о распространении световых волн вблизи препятствий, принцип Гюйгенса-Френеля следует дополнить постулатом Френеля о граничных условиях.

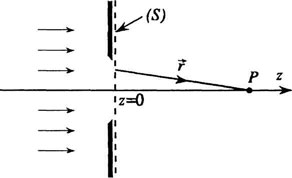Рис.2. Граничные условия.

Пусть на экран с отверстием падает плоская волна (рис.2). Постулат Френеля сводится к требованию заселения вторичными источниками только той части поверхности волнового фронта, которая не затенена экраном. При этом там, где поверхность S затенена экраном, амплитуда вторичных волн равна нулю. На открытых частях экрана поле первичной волны предполагается невозмущенным.

Постулат Френеля, как и принцип Гюйгенса–Френеля, носит приближенный характер. Его применение сильно упрощает дифракционную задачу и приводит к достаточно хорошим для практики результатам при условии, что размеры препятствий, на которых дифрагирует свет, а также расстояние между препятствием и точкой наблюдения велики по сравнению с длиной волны.

На основе принципа Гюйгенса-Френеля удается получить простое наглядное решение некоторых дифракционных задач (задачи с осевой симметрией, дифракция на одномерных препятствиях).

Дифракционные задачи с сетевой симметрией

Пусть плоская волна с амплитудой А₀ нормально падает на экран с круглым отверстием радиуса R (рис.3). Требуется найти поле в некоторой точке P на оси системы, находящейся на расстоянии z = b от экрана. Осевая симметрия резко упрощает решение задачи.

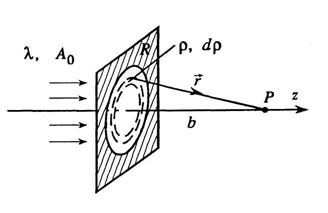Рис.3. Дифракция на круглом отверстии.

При качественном рассмотрении задачи удобно использовать метод векторных диаграмм. Элементарное колебание можно изобразить на векторной диаграмме с помощью вектора длины, ориентированного под углом по отношению к горизонтальной линии.

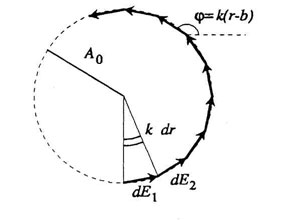Рис.4. Векторная диаграмма.

Считая dr достаточно малым, но конечным приращением длины радиуса-вектора, можно изобразить на векторной диаграмме колебания в точке наблюдения, создаваемые вторичными источниками, заселяющими различные элементарные кольца в плоскости экрана. В результате получим ломанную цепочку векторов. Если перейти к пределу dr→0 , то вместо ломанной линии получим окружность. Соответствующие различным значениям r окружности в плоскости экрана принято называть границами зон Френеля, а кольца, заключенные между соседними границами – зонами Френеля. Рис.5 поясняет принцип построения зон Френеля.