Способ анализа граничных значений
Как правило, большая часть ошибок происходит на границах области ввода, а не в центре. Анализ граничных значений заключается в получении тестовых вариантов, которые анализируют граничные значения [3], [14], [69]. Данный способ тестирования дополняет способ разбиения по эквивалентности.
Основные отличия анализа граничных значений от разбиения по эквивалентности:
1) тестовые варианты создаются для проверки только ребер классов эквивалентности;
2) при создании тестовых вариантов учитывают не только условия ввода, но и область вывода.
Сформулируем правила анализа граничных значений.
1. Если условие ввода задает диапазон п...т, тотестовые варианты должны быть построены:
q для значений п и т;
q для значений чуть левее п ичуть правее т на числовой оси.
Например, если задан входной диапазон -1,0...+1,0, то создаются тесты для значений - 1,0, +1,0, - 1,001, +1,001.
2. Если условие ввода задает дискретное множество значений, то создаются тестовые варианты:
q для проверки минимального и максимального из значений;
q для значений чуть меньше минимума и чуть больше максимума.
Так, если входной файл может содержать от 1 до 255 записей, то создаются тесты для О, 1, 255, 256 записей.
3. Правила 1 и 2 применяются к условиям области вывода.
Рассмотрим пример, когда в программе требуется выводить таблицу значений. Количество строк и столбцов в таблице меняется. Задается тестовый вариант для минимального вывода (по объему таблицы), а также тестовый вариант для максимального вывода (по объему таблицы).
4. Если внутренние структуры данных программы имеют предписанные границы, то разрабатываются тестовые варианты, проверяющие эти структуры на их границах.
5. Если входные или выходные данные программы являются упорядоченными множествами (например, последовательным файлом, линейным списком, таблицей), то надо тестировать обработку первого и последнего элементов этих множеств.
Большинство разработчиков используют этот способ интуитивно. При применении описанных правил тестирование границ будет более полным, в связи с чем возрастет вероятность обнаружения ошибок.
Рассмотрим применение способов разбиения по эквивалентности и анализа граничных значений на конкретном примере. Положим, что нужно протестировать программу бинарного поиска. Нам известна спецификация этой программы. Поиск выполняется в массиве элементов М, возвращается индекс I элемента массива, значение которого соответствует ключу поиска Key.
Предусловия:
1) массив должен быть упорядочен;
2) массив должен иметь не менее одного элемента;
3) нижняя граница массива (индекс) должна быть меньше или равна его верхней границе.
Постусловия:
1) если элемент найден, то флаг Result=True, значение I — номер элемента;
2) если элемент не найден, то флаг Result=False, значение I не определено.
Для формирования классов эквивалентности (и их ребер) надо произвести разбиение области ИД — построить дерево разбиений. Листья дерева разбиений дадут нам искомые классы эквивалентности. Определим стратегию разбиения. На первом уровне будем анализировать выполнимость предусловий, на втором уровне — выполнимость постусловий. На третьем уровне можно анализировать специальные требования, полученные из практики разработчика. В нашем примере мы знаем, что входной массив должен быть упорядочен. Обработка упорядоченных наборов из четного и нечетного количества элементов может выполняться по-разному. Кроме того, принято выделять специальный случай одноэлементного массива. Следовательно, на уровне специальных требований возможны следующие эквивалентные разбиения:
1) массив из одного элемента;
2) массив из четного количества элементов;
3) массив из нечетного количества элементов, большего единицы.
Наконец на последнем, 4-м уровне критерием разбиения может быть анализ ребер классов эквивалентности. Очевидно, возможны следующие варианты:
1) работа с первым элементом массива;
2) работа с последним элементом массива;
3) работа с промежуточным (ни с первым, ни с последним) элементом массива.
Структура дерева разбиений приведена на рис. 7.3.
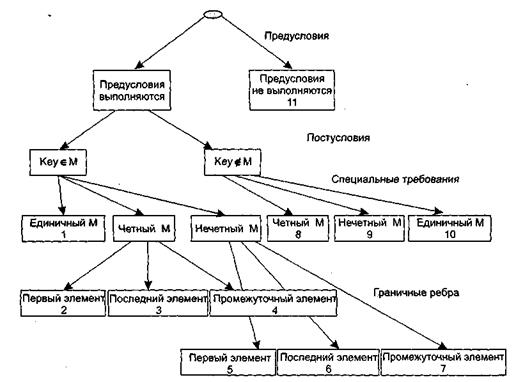
Рис. 7.3.Дерево разбиений области исходных данных бинарного поиска
Это дерево имеет 11 листьев. Каждый лист задает отдельный тестовый вариант. Покажем тестовые варианты, основанные на проведенных разбиениях.
Тестовый вариант 1 (единичный массив, элемент найден) ТВ1:
ИД: М=15; Кеу=15.
ОЖ.РЕЗ.: Resutt=True; I=1.
Тестовый вариант 2 (четный массив, найден 1-й элемент) ТВ2:
ИД: М=15, 20, 25,30,35,40; Кеу=15.
ОЖ.РЕЗ.: Result=True; I=1.
Тестовый вариант 3 (четный массив, найден последний элемент) ТВЗ:
ИД: М=15, 20, 25, 30, 35, 40; Кеу=40.
ОЖ.РЕЗ:. Result=True; I=6.
Тестовый вариант 4 (четный массив, найден промежуточный элемент) ТВ4:
ИД: М=15,20,25,30,35,40; Кеу=25.
ОЖ.РЕЗ.: Result-True; I=3.
Тестовый вариант 5 (нечетный массив, найден 1-й элемент) ТВ5:
ИД: М=15, 20, 25, 30, 35,40, 45; Кеу=15.
ОЖ.РЕЗ.: Result=True; I=1.
Тестовый вариант 6 (нечетный массив, найден последний элемент) ТВ6:
ИД: М=15, 20, 25, 30,35, 40,45; Кеу=45.
ОЖ.РЕЗ.: Result=True; I=7.
Тестовый вариант 7 (нечетный массив, найден промежуточный элемент) ТВ7:
ИД: М=15, 20, 25, 30,35, 40, 45; Кеу=30.
ОЖ.РЕЗ.: Result=True; I=4.
Тестовый вариант 8 (четный массив, не найден элемент) ТВ8:
ИД: М=15, 20, 25, 30, 35,40; Кеу=23.
ОЖ.РЕЗ.: Result=False; I=?
Тестовый вариант 9 (нечетный массив, не найден элемент) ТВ9;
ИД: М=15, 20, 25, 30, 35, 40, 45; Кеу=24.
ОЖ.РЕЗ:. Result=False; I=?
Тестовый вариант 10 (единичный массив, не найден элемент) ТВ10:
ИД: М=15; Кеу=0.
ОЖ.РЕЗ.: Result=False; I=?
Тестовый вариант 11 (нарушены предусловия) ТВ11:
ИД: М=15, 10, 5, 25, 20, 40, 35; Кеу=35.
ОЖ.РЕЗ.: Аварийное донесение: Массив не упорядочен.
