Арифметический цикл с рекуррентной зависимостью
Решение задач с циклическими вычислительными процессами
Циклы с параметром. Оператор FOR
Вычисление конечных сумм и произведений
Задача 1. Вычислить сумму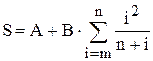 
. Значения величин A, B, m и n ввести с клавиатуры.
Алгоритм решения этой задачи очевиден, и наглядно описывается с приведенной на рис. 4.1 блок-схемой.
Код программы:
Sub pr1()
Dim A As Double, B As Double, S As Double
Dim n As Integer, m As Integer, i As Integer
A = InputBox(“A=“)
B = InputBox(“B=“)
m = InputBox(“m=“)
n = InputBox(“n=“)
For i = m To n
S = S + i ^ 2 / (n + i)
Next i
S = A + B * S
MsgBox(“S= “ & S)
EndSub
 |
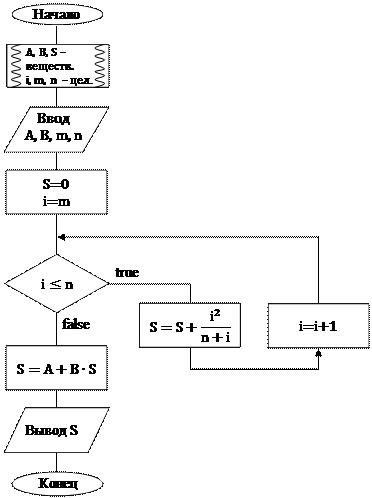Рис. 4.1. Блок-схема алгоритма решения задачи 1
Задача 2. Найти сумму S всех целых чисел, кратных 3 на отрезке [M, N].
Эта задача похожа на предыдущую. Отличие состоит в том, что, просматривая все числа из интервала [M, N], мы должны проверить, делится ли число i без остатка на 3 прежде, чем его суммировать к S. Для проверки деления используется операция mod – деление с остатком целых чисел, в результате выполнения которой получаем остаток от деления в виде целого числа. Таким образом, условие деления числа i на 3 без остатка будет иметь вид: i mod 3 = 0.
Алгоритм решения этой задачи отличен от предыдущего наличием условия в теле арифметического цикла, и описан с помощью приведенной ниже блок-схемы (рис. 4.2).
 |
Рис. 4.2. Блок-схема алгоритма решения задачи 2
Код программы:
Sub pr2()
Dim M As Double, N As Double, S As Double
Dim i As Integer
M = InputBox(“M=“)
N = InputBox(“N=“)
For i = M To N
If i Mod 3 = 0 Then S = S + i
Next i
MsgBox(“S= “ & S)
End Sub
Задача 3. Для заданного значения N найти 
.
Для вычисления Y, необходимо сделать следующие преобразование исходной формулы:
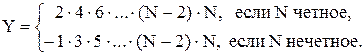(1)
Блок-схема алгоритма представлена на рис. 3.
 |
Рис. 3. Блок-схема алгоритма решения задачи 3
Код программы:
Sub pr3()
Dim Y As Double, i As Integer, N As Integer
N = InputBox(“Введите N“)
Y = 1
For i = 0 To (N – 1) \ 2
If N Mod 2 = 1 Then
Y = Y * (2 * i + 1)
Else
Y = Y * 2 * (i + 1)
End If
Next i
If N Mod 2 = 1 Then Y = - Y
MsgBox(“Y= “ & Y)
End Sub
Вложенный арифметический цикл
Под вложенным арифметическим циклом понимают такую алгоритмическую структуру, при которой в тело одного цикла с параметром включен другой цикл со своим параметром. Другими словами составная инструкция вида
FOR I = …
FOR J = …
FOR K = …
является признаком вложенного арифметического цикла.
Задача 4.Вычислить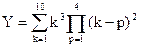 
.
Блок-схема алгоритма решения задачи представлена на рис. 4.
Код программы:
Sub pr4()
Dim Y As Double, Pr As Double, k As Integer, p As Integer
k = InputBox(“Введите k=“)
p = InputBox(“Введите p=“)
For k = 1 To 10
Pr = 1
For p = 1 To 4
Pr = Pr * (k – p) ^ 2
Next p
Y = Y + k ^ 3 * Pr
Next k
MsgBox(“Y= “ &Y)
End Sub
 |
Рис. 4. Блок-схема алгоритма решения задачи 4
Итерационные циклы
Итерационные циклы чаще всего используются для вычисления бесконечных сумм, бесконечных произведений и пределов функций и рядов.
Задача 5.Вычислить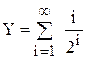 
. Вычисления остановить при выполнении условия 
.
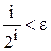Для решения этой задачи удобно использовать оператор цикла с предусловием Do While.
Блок-схема алгоритма решения задачи представлена на рис. 4.
Код программы – процедура pr5.
 |
Рис. 5 Блок-схема алгоритма решения задачи 5
Sub pr5()
Dim Y As Double, E As Double, i As Integer
E = InputBox(“Введите погрешность вычислений”)
i = 1 : Y = 0
Do While i/2^i >= E
Y = Y + i /2^2
i = i + 1
Loop
MsgBox(“Y=” & Y)
End Sub
Рекуррентные формулы
Арифметический цикл с рекуррентной зависимостью
Многие циклические вычислительные процессы используют рекуррентные зависимости при решении различных математических задач. В общем виде формулу для рекуррентных вычислений можно представить так:
(2)
В этой рекуррентной формуле для вычисления i -го члена последовательности 
, где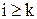 
, используются k предыдущих членов последовательности 
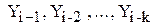. Для вычислений по формуле (2) нужно задать k первых членов последовательности - 
.
В ряде случаев рекуррентную формулу легко вывести. Например, для суммы ряда, описанной формулой S =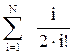 
, рекуррентная формула выводится из отношения текущего члена ряда к предыдущему.
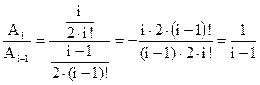(1)
Из (1) и находится рекуррентная формула:
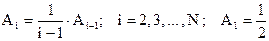(2)
Использование рекуррентных формул, как правило, сокращает текст программы и время выполнения на компьютере. Однако, в большинстве случаев, рекуррентную формулу нужно написать программисту, что в ряде случаев вызывает определенные трудности. Один из таких случаев рассмотрен в решении задачи 6.
Задача 6. Вычислить значение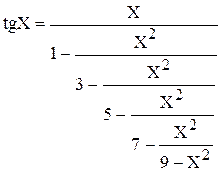 
.
Знаменатель формулы для вычисления tgX представляет собой цепную дробь. Для вычисления такого знаменателя в цикле удобно использовать рекуррентную зависимость с памятью в один член последовательности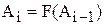 
. Для вывода рекуррентной формулы следует использовать табл. 1.
Таблица 1
| Номер i | Член последовательности | Величина |
 | ||
 |  | |
 |  | |
 |  | |
 |  | |
 |  |
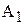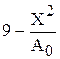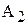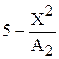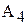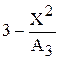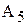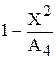Из табл. 1 легко заметить, что рекуррентная формула принимает вид:
(3)
Блок-схема алгоритма решения задачи представлена на рис. 6.
Код программы представлен процедурой pr6.
Код программы:
Sub pr6()
Dim X As Double, A As Double; i As Integer
X=InputBox(“Введите X”)
A = 1
For i = 1 TO 5
A =11 - 2*i- X*X/A
Next i
MsgBox(“tg X = ” & Format(A, “fixed”))
End Sub
Рис. 6 Блок-схема алгоритма решения задачи 6
Задача 7.Пользуясь рекуррентной формулой, для заданного N вычислить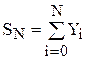 
, если известны 
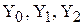, а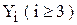 
вычисляется по формуле
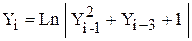(4)
Таблица имён
| Математ.величина | Обозначениев программе | Содержательный смысл | Типпеременной |
| i | i | Номер текущего члена последовательности | integer |
| N | N | Номер последнего члена последовательности | integer |
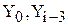 | Y3 | Член последовательности с номером i-3 | double |
 | Y2 | Член последовательности с номером i-2 | double |
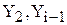 | Y1 | Член последовательности с номером i-1 | double |
| | Y | Член последовательности с номером i | double |
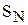 | S | Искомая сумма | double |
Первым шагом в работе алгоритма является ввод данных Y0, Y1, Y2, N. При вводе трех первых значений последовательности нужно использовать рабочие ячейки Y3, Y2 и Y1, соответственно. На втором шаге требуется проанализировать значение N. Если N < 3, то рекуррентная формула для подсчета S суммы первых N членов не потребуется. Для определения S при условии N < 3, в алгоритме предусмотрен переключатель (оператор Select Case), имеющий три ветви: N = 0, N = 1, в противном случае (куда попадает и случай N = 2). Для каждой ветви подсчитывается соответствующая сумма S. Третий шаг выполняется только в том случае, если N > 2. На этом шаге для I от 3 до N по рекуррентной формуле вычисляются YI и подсчитывается их сумма S. Найденное значение S на последнем четвертом шаге выводится на экран.
Блок-схема алгоритма решения задачи представлена на рис. 7.
Код программы представлен процедурой pr7.
Sub pr7()
Dim Y3 As Double, Y2 As Double, Y1 As Double, Y As Double
Dim S As Double
Dim N As Integer, i As Integer
Y3=InputBox(“Введите Y0”)
Y2=InputBox(“Введите Y1”)
Y1=InputBox(“Введите Y2”)
N=InputBox(“Введите N”)
Select Case N
Case 0
S=Y3
Case 1
S=Y3+Y2
Case Else
S=Y3+Y2+Y1
End Select
If N>2 Then
For i=3 To N
Y=Log(Abs(Y1*Y1+Y3+1)
S=S+Y
Y3=Y2
Y2=Y1
Y1=Y
Next i
End If
MsgBox(“S = ” & Format(S, “fixed”))
End Sub
 |
Рис. 7. Блок-схема алгоритма решения задачи 7