Определения и условные обозначения
Ниже даются определения доверительного интервала и других статистических понятий, которые играют главную роль в определении объема выборки.
Параметр (parameter) — это описание определенной характеристики изучаемой совокупности. Параметр указывает на истинное значение, которое было бы получено, если бы проводилась перепись, а не выборка.
Статистика (statistic) — описание характеристики выборки. Статистика выборки используется для оценки параметров генеральной совокупности.
Окончательная коррекция совокупности (finite population correction, fpc) — это коррекция, применяемая для перерасчета дисперсии параметра генеральной совокупности, например среднего или доли, если объем выборки составляет 10% или больше от объема популяции.
Степень точности (precision level) — это желательная величина оценочного интервала при оценке параметра совокупности с использованием выборочной статистики. Это максимально допустимое различие между статистикой выборки и параметром генеральной совокупности.
Доверительный интервал (confidence interval) — это диапазон, в который попадет истинное значение параметра совокупности при данном уровне достоверности.
Уровень достоверности (confidence level) — это вероятность того, что параметр совокупности попадет в доверительный интервал.
Символы, применяемые в системе статистических обозначений для описания характеристик генеральной совокупности и выборки, представлены в табл. 12.1.
| Таблица 12.1. Условные обозначения для переменных генеральной совокупности и выборки | ||
| Переменная | Совокупность | Выборка |
| Среднее Доля Дисперсия Среднеквадратичное (стандартное) отклонение Объем Стандартная ошибка среднего Стандартная ошибка доли Нормированная величина (z) Коэффициент вариации (С) | µ π σ2 σ Ν σх- σp Χ-μ σ σ μ | 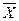 P s2 s n P s2 s n 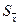 Sp Χ- Sp Χ- 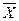 S S X1 S S X1 |
ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ
Выборочное распределение(sampling distribution) — это распределение значений выборочных статистик, рассчитанных для каждой возможной выборки, которая формируется из изучаемой совокупности при определенном плане выборочного наблюдения [3]. Предположим, что простую случайную выборку, включающую 5 больниц, нужно сформировать из генеральной совокупности 20 больниц. Можно получить (20 х 19 х 18 х 17 х 16)/(1 х 2 х 3 х 4 х 5), или 15504 различных выборок каждая размером в 5 элементов. Распределение относительных частот средних значений этих 15504 различных выборок определяет выборочное распределение среднего.
