Задания для самостоятельного выполнения
Методические указания к выполнению лабораторной работы
Программирование алгоритмов циклической структуры.
Оператор цикла с предусловием
Цель работы: освоить методику программирование циклических алгоритмов в АВС Pascal.
Программное обеспечение: система программирования АВС Pascal.
Теоретические сведения
Оператор цикла с предусловием используется в случае, когда число повторений цикла заранее не известно. При этом цикл управляется условием, записанным в начале цикла, и поэтому действия в цикле при некотором условии могут ни разу не выполниться. Структура этого оператора имеет вид
WHILE <условие> DO <оператор>;
где <условие> – это любое логическое выражение для параметра цикла, истинность которого проверяется в начале каждой итерации (условие выполнения тела цикла), <оператором> может быть произвольный оператор языка, в том числе и составной.
Правило выполнения оператора цикла с предусловием. Если <условие> истинно, то выполняется <оператор>, стоящий за ключевым словом DO, если <условие> ложно, то происходит выход из цикла и выполняется следующий оператор программы. После выполнения <оператора> вновь вычисляется и анализируется <условие>, и вновь, в случае его истинности, выполняется <оператор> в цикле. Эти действия повторяются до тех пор, пока <условие> не станет ложным. Поскольку параметр цикла используется для управления циклом, необходимо изменять этот параметр внутри составного оператора цикла.
Пример. Вычислить Y = 1+1/2+1/3+...+1/N. Фрагмент программы с применением оператора WHILE может быть составлен в следующем виде:
Y:=0; I:=1;
WHILE I<= N DO
begin
Y:=Y+1/I;
I:=I+1
end;
Примеры
Пример 1. Программа, которая производит суммирование 10 произвольно введенных целых чисел.
Program Exp_3;
Const Limit=10;
VarI, A, Sum: Integer;
Begin
I:=0; { Счетчик чисел }
Sum:=0; { Сумма чисел }
While( I< Limit ) Do { Условие выполнения цикла}
Begin
I:= I + 1;
Write ( ‘ Введите ‘, I, ‘ – ое целое число : ‘);
Readln ( A ); { Ввод очередного числа с клавиатуры }
Sum:= Sum + А;
End;
Writeln ( ‘ Сумма введенных чисел равна ‘ , Sum);
End.
В данном примере в разделе описания констант описана константа Limit=10, задающая ограничение на количество вводимых чисел. В разделе описания переменных описаны переменные I, A, Sum целочисленного типа.
В начале выполнения программы обнуляются значения счетчика введенных чисел I и их суммы.
Затем выполняются цикл ввода десяти чисел и их суммирование. Вначале оператор условия While проверяет условие I<Limit. Если условие истинно, то выполняется составной оператор в теле цикла:
Begin
I:= I +1;
Write ( ‘Введите ‘, I, ‘ – ое целое число : ‘);
Readln ( A );
Sum:= Sum + А;
End;
в котором вводится значение очередного числа, и на это значение увеличивается значение суммы. После этого управление в программе вновь передается оператору цикла While, опять проверяется условие I<Limit. Если условие истинно, то выполняется составной оператор и т.д., пока значение переменной I будет меньше 10.
Как только значение I станет равно 10 и условие I<Limit не будет соблюдено, выполнение цикла завершится, а управление в программе будет передано оператору, находящийся за словом End, т.е. первый оператор за границей While. Это вызов процедуры Writeln, которая выведет сообщение ‘Сумма введенных чисел равна ‘, и напечатает значение переменной Sum.
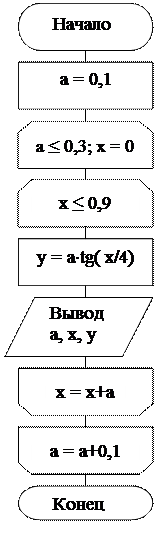 |
Пример2. Для трех значений а = 0.1, 0.2, 0.3 протабулировать функцию y = a.tg(x/4) при изменении аргумента x на интервале [0.5,0.9] с шагом, равным a. Для алгоритма решения данной задачи (рисунок 1) программа может быть следующей:
Program tab;
var a, x, y: real; {а≤0,3;х=0}
Begin
writeln('-------------------------');
writeln(' a | x | y |');
writeln('-------------------------');
a:= 0.1;
while a<=0.31 do
begin
writeln(a:5:2);
x :=0.5;
while x<=0.9 do
begin
y :=a*sin(x/4) / cos(x/4);
writeln(x:12:2,' | ', y:10:2);
x :=x+a;
end;
writeln('-------------------------');
a:=a+0.1
end;
End.
Задания для самостоятельного выполнения
Задание 1. Построить алгоритм, написать и отладить программу. Использовать операции деления нацело и взятия остатка от деления.
1. Найти сумму цифр целого числа.
2. Найти произведение цифр целого числа.
3. Найти количество нечетных цифр целого числа.
4. Найти первую цифру числа.
5. Поменять порядок цифр числа на обратный. Например, было 12345, стало 54321.
6. Найти количество четных цифр целого положительного числа.
7. Сколько цифр в данном числе больше числа 5?
8. Найти самую большую цифру целого положительного числа.
9. Сколько раз цифра 5 встречается в целом числе.
10. Найти количество нечетных цифр в целом числе.
11. Найти сумму четных цифр целого числа.
12. Найти произведение нечетных цифр целого числа.
13. Найти самую маленькую цифру целого числа.
14. Верно ли, что в данном числе нет цифры 6?
15. Верно ли, что сумма цифр данного числа равна 20?
16. Найти количество цифр данного числа, больших А.
17. Сколько раз последняя цифра встречается в данном числе.
18. Верно ли, что последняя цифра данного числа нечетная?
19. Сколько раз встречается в данном числе цифра 8?
20. Сколько цифр в данном числе меньше цифры 5?
21. Верно ли, что сумма цифр данного числа меньше 30?
22. Сколько цифр в данном числе меньше цифры 6.
23. Сколько раз в данном числе встречается цифра 3.
24. Найти сумму нечетных цифр целого числа.
25. Найти произведение четных цифр целого числа.
26. Составить программу, проверяющую, является ли заданное натуральное число палиндромом, то есть таким, десятичная запись которого читается одинаково слева направо и справа налево, например, числа 2222, 1331, 6006.
Задание 2. Начертите структурную схему алгоритма, напишите и отладьте программу для табуляции следующих функций:
| № варианта | Функция | Условия | |
| 1. | 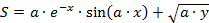 | a = 0.75, -1 ≤ x ≤ 1 с шагом 0.2, 1 ≤ y ≤ 5 с шагом 1.5. | |
| 2. | 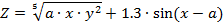 | a = 1.9, 2 ≤ x ≤ 5 с шагом 0.5, -1 ≤ y ≤ 1 с шагом 0.5. | |
| 3. | 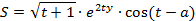 | a = -2.1, 1 ≤ t ≤ 2 с шагом 0.2, 2 ≤ y ≤ 3 с шагом 0.3. | |
| 4. | 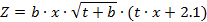 | b = 3.5, 1 ≤ x ≤ 2 с шагом 0.2, 0 ≤ t ≤ 1 с шагом 0.2. | |
| 5. | 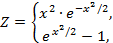 | если 0 ≤ x ≤ 2, если 2 < x ≤ 3.6 | а = 0.5; 0.75, шаг dx = а/2. |
| 6. | 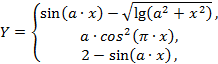 | если 0.1 ≤ x ≤ 0.4, если 0.4 < x ≤ 1.2, если 1.2 < x ≤ 1.6 | а = 1.0; 1.5, шаг dx = а/5. |
| 7. | 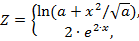 | если 0 ≤ x ≤ 2, если 2 < x ≤ 3.6 | а = 1.0; 1.3; 1.6, шаг dx = а/4. |
| 8. | 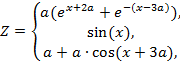 | если 0.1 ≤ x < 0.5, если x = 0.5, если 0.5 < x ≤ 1.5 | а = 2.0; 2.1, шаг dx = а/10. |
| 9. | 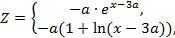 | если 0 < x ≤ 3, если 3 < x ≤ 4 | а = 1.0; 1.5, шаг dx = а/2. |
| 10. | 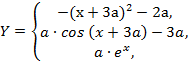 | если -1 ≤ x ≤ 0, если 0 < x < 1, если x = 1 | а = 0.7; 1, шаг dx = (а+0.2)/2. |
| 11. | 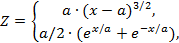 | если 1 ≤ x ≤ 2.5, если 2.5 < x ≤ 4 | а = 0.5; 1.0, шаг dx = а/2. |
| 12. | 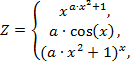 | если 0.5 ≤ x < 1.5, если x = 1.5, если 1.5 < x ≤ 3 | а = 0.1; 0.2; 0.3, шаг dx = 2а. |
| 13. | 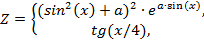 | если 0.1 ≤ x ≤ 0.5, если 0.5 < x ≤ 0.9 | а = 0.1; 0.2; 0.3, шаг dx = а. |
| 14. | 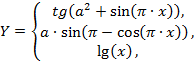 | если 0 ≤ x ≤ 1, если 1 < x ≤ 2, если 2 < x < 3 | а = 0.5; 0.75; 1.0, шаг dx = а/4. |
| 15. | 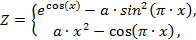 | если 0.5 ≤ x ≤ 1.5, если 1.5 < x ≤ 2 | а = 0.1; 0.7; 1.3, шаг dx = а/4. |
| 16. | 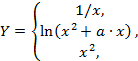 | если 0.1 ≤ x ≤ 0.4, если 0.4 < x ≤ 1.2, если 1.2 < x < 1.6 | а = 1.0; 1.5, шаг dx = а/5. |
17. Дана непустая последовательность различных натуральных чисел, за которой следует нуль (признак конца последовательности). Определить порядковый номер наименьшего из них и его значение.
18. Найти первый отрицательный член последовательности cos(ctg(n)), где n = 1, 2, 3, ..., x. Напечатать его номер и значение. Распечатать всю последовательность.
19. Вычислить наибольший общий делитель (k) натуральных чисел d и f. Оператор FOR не использовать.
20. Задан ряд неотрицательных вещественных чисел. Определить, сколько из них больше своих «соседей»: предыдущего и последующего чисел. Признаком окончания ряда чисел считать появление отрицательного числа.
