Н.С.В. Функция распределения
Случайную величину Х называют непрерывной (непрерывно распределенной) величиной, если существует такая неотрицательная функция p(t), определенная на всей числовой оси, что для всех х функция распределения случайной величины F(x) равна:
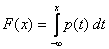 . (6.7)
. (6.7)
При этом функция p(t) называется плотностью распределения вероятностейнепрерывной случайной величины.
Если такой функции p(t) не существует, то Х не является непрерывно распределенной случайной величиной.
Таким образом, зная плотность распределения, по формуле (6.7) можно легко найти функцию распределения F(x). И, наоборот, по известной функции распределения можно восстановить плотность распределения:
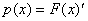 .
.
Значит, наряду с функцией распределения, плотность распределения вероятностей непрерывной случайной величины задает ее закон распределения.
Плотность распределения Н.С.В.
Свойства плотности распределения вероятностей
непрерывной случайной величины:
1. Плотность распределения – неотрицательная функция:
P(t)³0.
Геометрически это означает, что график плотности распределения расположен либо выше оси Ох, либо на этой оси.
2. 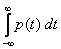 =1.
=1.
Учитывая, что F(+¥)=1, получаем: 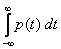 =1. Т.е. площадь между графиком плотности распределения вероятностей и осью абсцисс равна единице.
=1. Т.е. площадь между графиком плотности распределения вероятностей и осью абсцисс равна единице.
Эти два свойства являются характеристическими для плотности распределения вероятностей. Доказывается и обратное утверждение:
Любая неотрицательная функция p(t), для которой 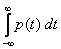 =1, является плотностью распределения вероятностей некоторой непрерывно распределенной случайной величины.
=1, является плотностью распределения вероятностей некоторой непрерывно распределенной случайной величины.
Общий вид графика функции плотности распределения вероятностей непрерывной случайной величины приведен на рис. 6.7.
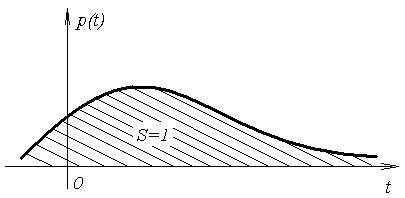 Рис. 6.7
Рис. 6.7
Зная плотность распределения, можно вычислить вероятность попадания значений непрерывной случайной величины в заданный интервал.
Вероятность того, что непрерывная случайная величина примет значения, принадлежащие интервалу (a, b), равна определенному интервалу от плотности распределения, взятому в пределах ота до b:
P(а£Х<b)= 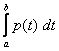 .
.
Действительно, P(а£Х<b)=F(b) – F(a)= 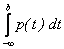 –
– 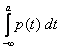 =
= 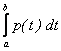 по одному из свойств определенного интеграла.
по одному из свойств определенного интеграла.
Из вышеприведенного утверждения можно сделать вывод, что вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю. Отсюда,
P(a£Х<b)=P(a<Х<b)=P(a<Х£b)=P(a£Х£b)=F(b) – F(a).
Геометрически вероятность попадания значений непрерывной случайной величины в интервал (a, b) может быть рассмотрена как площадь фигуры, ограниченной осью Ох, графиком плотности распределенияp(t) и прямыми х=a и х=b (рис. 6.8).
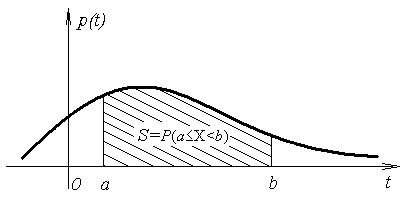
Рис. 6.8
Определения числовых характеристик случайной величины, рассмотренные в параграфе 6.2, можно распространить на случай непрерывной величины.
Математическим ожиданием непрерывной случайной величины называется несобственный интеграл
М[X] = 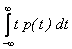 .
.
Если возможные значения случайной величины принадлежат отрезку [a,b], то М[X]= 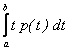 .
.
Используя определение дисперсии (6.4) для случая непрерывной случайной величины, можно получить следующую формулу для вычисления дисперсии
D[X] = 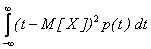 .
.
Если возможные ненулевые значения случайной величины принадлежат отрезку [a, b], то
D[X] = 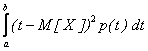 .
.
Более удобные формулы для вычисления дисперсии таковы:
D[X] = 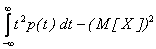 ,
,
если функция p(t) отлична от 0 на всей числовой оси;
D[X] = 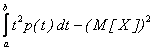 (6.8)
(6.8)
если возможные ненулевые значения случайной величины принадлежат отрезку [a,b].
Среднее квадратическое отклонение непрерывной случайной величины определяется также, как и для случая дискретной случайной величины:
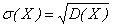 .
.
Пример 6.8 .Плотность вероятности непрерывной случайной величины Х равна
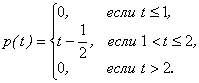
Найти функцию распределения F(X), математическое ожидание, дисперсию и среднее квадратическое отклонение величины Х.
Построим функцию распределения случайной величины Х, используя формулу (6.7).
При х£1, 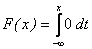 =0.
=0.
Если 1£х£2, 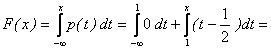 0+
0+ 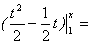
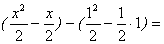
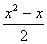 .
.
При х>2,
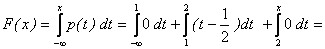 0+
0+ 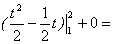
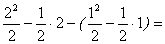 2–1=1.
2–1=1.
Значит, 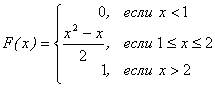 .
.
Математическое ожидание случайной величины Х равно:

Дисперсию величины Х находим по формуле (6.8):
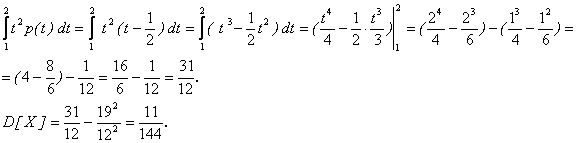
Среднее квадратическое отклонение величины Х равно: