Итерационные циклы с приближенным решением

Количество задач, реализуемых итерационными циклами с точным решением невелико. Значительно больше задач, в которых решение стремится к точному значению функции, но достигнуть его не может, т.е. обуславливающих итерационные циклы с приближенным решением.

Типичные представители этой группы – вычисления тригонометрических функций (реализуемых стандартными подпрограммами), вычисления степенных рядов и т. д. Характерная особенность таких задач – соединение простого итерационного цикла с накоплением. Поэтому типовые методики предмашинной подготовки этих задач изложены в соответствующей – следующей главе. Ниже рассматриваются «чистые» итерационные задачи с приближенным решением. Первая из них – задача (7.3) о вычислении произведений.

Задача вычисления произведений

Постановка задачи

Даны два одномерных массива одинакового размера, численные значения которых увеличиваются по мере увеличения индексов. Рассчитать произведения попарных элементов. Расчёт производить до тех пор, пока частное от деления заданной переменной х на полученное текущее значение не станет меньше некоторой минимальной величины (e).

Формирование математической модели

Исходные данные

|a₁ a₂ . . . a_i . . . a_n| – модель первого исходного массива;

|b₁ b₂ . . . b_i . . . b_n| – модель второго исходного массива;

x = _ _ _ , _ _ _ – переменная (делимое);

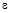= _ , _ _ _ _ – предел (граница) вычислений.

Расчётные зависимости

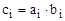– основная зависимость;

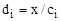– вспомогательная зависимость;

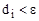– условие прекращения вычислений;

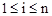– возможный диапазон изменения индекса;

i = i + 1 – закон изменения индекса.

Выбор метода решения

Анализ математической модели задачи показывает, что её решение требует многократного расчёта значений попарных произведений соответствующих элементов массивов. Вычисления необходимо производить до тех пор, пока частное от деления заданной переменной x на текущее значение произведения превышает заданное граничное значение 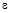( 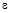= 0,005). Решение можно осуществить двумя вариантами:

· арифметическим циклом с искусственным выходом;

· итерационным циклом.

Первый из них в качестве основного параметра цикла использует индекс i, изменяющийся по стандартному закону i = i + 1. При этом желаемый выход из цикла определяется дополнительным условием ( 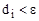), проверяемым в теле цикла.

Второй вариант требует вычислений основной и вспомогательной расчётных зависимостей с использованием дополнительной (i = i + 1), формирующей текущие значения индексов для вызова элементов массива, т. е. определяет выбор метода расчёта с аналитическим изменением аргумента – дополнительной переменной (индекса i).

Таким образом, для первого варианта параметром цикла является переменная i с указанным в математической формулировке законом изменения i = i + 1. При этом возможны два варианта прекращения цикла – естественный, после перебора всех элементов массива 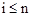(если условие выхода не выполняется) и основной – искусственный .

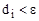Для второго варианта параметром цикла является переменная d_i с законом изменения 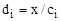. При этом процесс счёта необходимо осуществлять до тех пор, пока выполняется условие 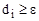, обратное заданному в постановке задачи ( 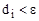) для прекращения вычислений.

Следовательно, в качестве численного метода решения требуется циклический вычислительный процесс с неизвестным числом повторений (итерационный) выполняемый до получения результата со значением, меньшим граничного.