Обратимое сжатие информации

Если при сжатии данных происходит только изменение их структуры, то метод сжатия обратим. Из результирующего кода можно восстановить исходный путем применения обратного метода. Обратимые методы применяют для сжатия любых типов данных. Характерными форматами сжатия без потери информации являются: GIF, TIP, PCX и многие другие для графических данных; AVI для видеоданных; ZIP, ARJ, RAR для любых типов данных.

Существует достаточно много обратимых методов сжатия данных, однако в их основе лежит сравнительно небольшое количество теоретических алгоритмов, представленных в следующей таблице:

Алгоритм	Выходная структура	Сфера применения	Примечание
RLE(Run Length Encoding)	Список (вектор данных)	Графические данные	Эффективность алгоритма не зависит от объема данных
KWE (Keyword Encoding)	Таблица данных (словарь)	Текстовые данные	Эффективность алгоритма не зависит от объема данных
Алгоритм Хаффмана	Иерархическая структура (дерево кодировки)	Любые данные	Эффективность алгоритма не зависит от объема данных

Алгоритм RLE

В основу алгоритма RLE положен принцип выявления повторяющихся последовательностей данных и замены их простой структурой, в которой указывается код данных и коэффициент повтора.

Пример 1.

Для последовательности данных вида:

0; 0; 0; 127; 127; 0; 255; 255; 255; 255 (всего 10 байтов)

при упаковке с использованием алгоритма RLE образуется другая последовательность:

0; 3; 127; 2; 0; 1; 255; 4 (всего 8 байтов).

В данном примере коэффициент сжатия равен 8/10 (80 %).

Программные реализации алгоритмов RLE отличаются простотой, высокой скоростью работы, но в среднем обеспечивают недостаточное сжатие. Наилучшими объектами для данного алгоритма являются графические файлы, в которых большие одноцветные участки изображения кодируются длинными последовательностями одинаковых байтов. Этот метод также может давать заметный выигрыш на некоторых типах файлов баз данных, имеющих таблицы с фиксированной длиной полей. Для текстовых данных методы RLE, как правило, неэффективны.

Алгоритм Хаффмана

После рассмотрения примера возникает вопрос: насколько оправдано использование целого байта для кодирования одного символа алфавита? Таким же вопросом задался американец Хаффман (Huffman), в 1952 году предложивший метод кодирования информации с помощью кодов переменной длины, который носит его имя даже несмотря на то, что с тех пор предложено большое количество усовершенствований этого метода и от него самого осталась лишь приблизительная схема. В основе этого метода лежит вероятностный подход к анализу появления символов используемого алфавита. Хорошо известно, что частота появления тех или иных символов алфавита неодинакова. Рассчитать вероятности появления символов не представляет трудности: для этого надо просто подсчитать количество символов каждого вида в достаточно большом тексте (чем больше текст, тем точнее расчётная вероятность), после чего символам, имеющим более высокие вероятности появления, назначаются более короткие коды, а тем символам, которые редко встречаются —более длинные. Рассмотрим пример.

Пример 2.

Пусть алфавит состоит из шести символов: <A>, <B>, <C>, <D>, <E> и <пробел>, и известно, что вероятность появления символов в тексте сообщений такова:

<пробел>	0,3
<A>	0,2
<B>	0,1
<C>	0,1
<D>	0,05
<E>	0,25

Если использовать стандартное двоичное кодирование символов алфавита, то на каждый символ потребуется [log₂6]+1=3 бита:

<пробел>
<A>
<B>
<C>
<D>
<E>

Для хранения 100-символьного сообщения потребуется тогда V_исх = 300 бит. Сравним, какой выигрыш мы получим, если применить метод Хаффмана для кодирования данных. Код может быть представлен в виде бинарного дерева, листьями которого являются символы алфавита, а узлами — точки принятия решения о выборе следующего символа кода.

Составим дерево кода Хаффмана. Исходный список символов алфавита с вероятностями появления имеет вид:

A	B	C	D	E	пробел
0,2	0,1	0,1	0,05	0,25	0,3

Уберём из исходного списка два элемента, имеющие наименьшие вероятности появления и сформируем ответвление по следующему правилу: в узле появится сумма вероятностей появления символов, а листьями станут сами эти символы:

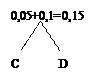	A	B	E	пробел
0,2	0,1	0,25	0,3

Повторим процедуру предыдущего шага и сформируем новый ярус из элементов, имеющих наименьшие значения вероятностей:

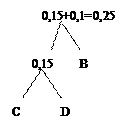	A	E	пробел
0,2	0,25	0,3

На этот раз формируем новое ответвление из элементов A и E:

		пробел
0,3

Объединим два элемента, имеющие наименьшие значения вероятностей:

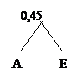Завершаем построение дерева:

Перекодируем символы алфавита в соответствии с построенным деревом:

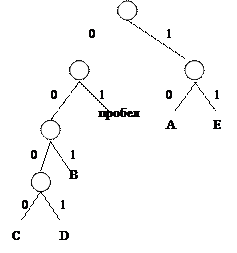Теперь таблица кодов будет выглядеть так:

<пробел>
<A>
<B>
<C>
<D>
<E>

Видно, что те символы, которые встречаются чаще, имеют короткий код, а те символы, которые встречаются редко — длинный (причём, чем реже, тем длиннее). Рассчитаем теперь, сколько бит потребуется для хранения 100-символьного сообщения при таком кодировании, учитывая вероятности появления символов и количество битов для каждого символа:

V_сж = 100*0,3*2+100*0,2*2+100*0,1*3+100*0,1*4+100*0,05*5+100*0,25*2=240

Для оценки эффективности сжатия воспользуемся такой формулой: 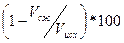%. Для нашего случая эффективность сжатия равна 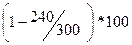%=20%.

Упаковка с потерей информации — используется для упаковки графических изображений. Этот метод основан на особенности человеческого восприятия изображений. Для человеческого глаза яркость более существенна, чем информация о цветовом фоне или насыщенности точки. Поэтому при упаковке можно выбросить данные о цвете каждой второй точки изображения (сохранив только её яркость), а при распаковке брать вместо выброшенного цвет соседней точки. Распакованная картинка будет отличаться от исходной, но отличие будет практически незаметно. За высокое качество упаковки приходиться платить большими затратами времени на распаковку. Алгоритмы, дающие очень хорошее качество упаковки, могут оказаться неприменимыми из-за слишком большого времени, требуемого на распаковку. Например, если время распаковки одного кадра фильма равно одной секунде, то такой фильм придётся смотреть только после предварительной распаковки.

Из всех видов информации, используемых в компьютерах, хуже всего поддаётся упаковке звук. Это связано с тем, что звуковые сигналы обладают малой избыточностью (в закодированных звуковых фрагментах редко попадаются повторяющиеся последовательности байтов). Даже методы упаковки с потерей информации не позволяют упаковать звук более чем в два раза без заметного снижения качества, тогда как графические изображения можно сжимать в десятки раз без потери качества изображения. Поэтому применяется метод компандирования: если повышать громкость звука в 2, 4, 8 и так далее раз, то человеческое ухо будет воспринимать это как линейное увеличение интенсивности звука. Значит, изменение громкости от 1 до 2 столь же заметно, сколько от 100 до 200, таким образом при компандировании значение амплитуды звука заменяется на логарифм этого значения. Полученные числа округляются и записываются в ячейки меньшей длины. Такое кодирование сжимает информацию как раз вдвое.