Глава 1. Элементы аналитической геометрии

Специфика математического аппарата компьютерной графики состоит в его исключительно практической направленности. Математические методы компьютерной графики предназначены для получения зрительно осязаемых результатов. Однако использование прикладных математических методов не освобождает от знания теоретических основ, из которых эти методы были получены. В данной главе рассматриваются элементы теории аналитической геометрии в трехмерном пространстве как поэтапное построение теоретических конструкций, происходящих из необходимости решения некоторых практических задач. Такой, в некотором смысле, неформальный подход позволяет рассматривать аналитическую геометрию не просто как раздел линейной алгебры, а как мощную методологию решения практических геометрических задач, возникающих в трехмерных и двумерных приложениях компьютерной графики.

Система координат

Для того чтобы уметь синтезировать изображения на экране компьютера необходимо предложить способ математического описания объектов в трехмерном пространстве или на плоскости. Окружающий нас мир с точки зрения практических приложений описывают как трехмерное евклидово пространство. Под описанием трехмерного объекта будем понимать знание о положении каждой точки объекта в пространстве в любой момент времени. Положение точек в пространстве удобно описывается с помощью декартовой системы координат.

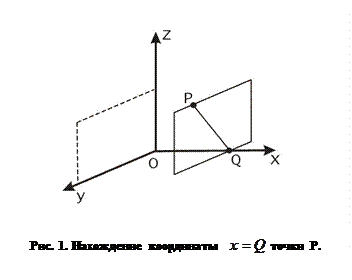Для того чтобы в трехмерном пространстве задать декартову систему координат проведем три не лежащие в одной плоскости направленные прямые, которые называются осями, так, чтобы они пересекались в одной точке – начале координат. Выберем на этих осях единицу измерения. Тогда положение любой точки в пространстве будет описываться через координаты этой точки, которые представляют собой расстояния от начала координат до проекций точки на соответствующие оси координат. Проекцией точки на координатную ось называется точка пересечения плоскости, проходящей через заданную точку и параллельной плоскости, образованной двумя другими осями координат. Например, на рис. 1 проекцией точки на ось является точка , которая принадлежит плоскости, параллельной плоскости .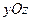

В общем случае оси системы координат могут располагаться под произвольными, хотя и фиксированными углами друг относительно друга. Для практических расчетов гораздо удобнее, когда эти оси расположены взаимно перпендикулярно. Такая система координат называется ортогональной. В ортогональной системе координат проекцией точки 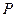на ось является единственная точка на оси такая, что отрезок прямой, проведенной из этой точки к точке 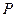, является перпендикулярным к данной оси.

Таким образом, положение в пространстве точки 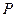описывается ее координатами, что записывается как 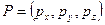. Взаимное расположение осей в ортогональной системе координат в трехмерном пространстве может быть двух видов. Проведем ось слева направо, а ось снизу вверх, как показано на рис. 2.

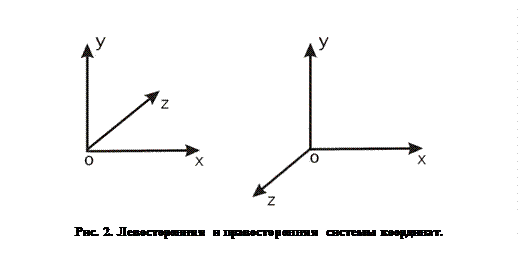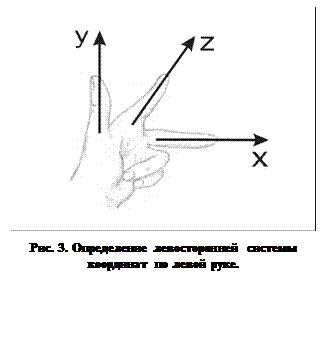
Ось 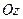при этом может проходить как в направлении от наблюдателя в плоскость листа, так и от плоскости листа к наблюдателю. В первом случае система координат будет называться левой или левосторонней, а во втором случае – правой или правосторонней. Более точное определение правой и левой систем координат можно дать следующее. Если посмотреть из положительной полуоси 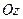в направлении начала координат, то для совмещения положительной полуоси 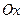с положительной полуосью 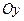необходимо повернуть 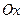относительно начала координат против часовой стрелки – в этом случае имеем правую систему координат; если же поворот производится по часовой стрелке – то система координат левая*.

Существует также легкий способ определения вида системы координат по правой или левой руке, как показано на рис. 3. Для левой руки большой, указательный и средний пальцы формируют левую тройку ортогональных векторов. То же относится и к их циклическим перестановкам.

Декартовы координаты точек позволяют описывать статичное положение точек в пространстве. Однако, для проведения каких-либо преобразований над объектами, которые описываются точками, необходимо иметь дополнительный математический аппарат. В качестве такого математического аппарата применяют радиус-векторы. Радиус-векторы обладают всеми свойствами векторов, но имеют одну особенность: начало радиус-вектора находится всегда в начале системы координат, а конец радиус-вектора лежит в некоторой точке пространства. Это свойство радиус-векторов позволяет поставить во взаимно однозначное соответствие всем точкам пространства соответствующие им радиус-векторы. Формально это соответствие запишем в следующем виде. 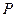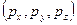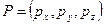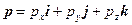Пусть точка имеет координаты , то есть , и – радиус-вектор, конец которого находится в точк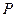е , где 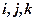– тройка единичных базисных векторов (ортов), или просто ортонормированный базис. Тогда точке 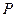взаимно однозначно соответствует радиус-вектор 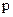, или 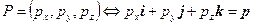. Таким образом, можно легко переходить от координат точек к радиус-векторам и обратно. Далее мы увидим, что представление радиус-вектора в виде линейной комбинации векторов базиса имеет вполне конкретное практическое применение. Отметим, что радиус-вектор иногда определяют как преобразование переноса точки из начала координат в заданную точку пространства с известными координатами. При этом умножение радиус-вектора 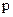на число 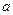соответствует переносу точки из начала координат в направлении вектора 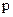на расстояние 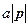, где в прямых скобках 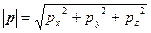– модуль вектора.

Сложение радиус-векторов 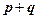можно рассматривать как перенос точки 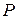по направлению вектора 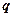на расстояние .

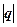Уравнение прямой

Рассмотрим, каким образом можно использовать координаты точек и радиус-векторы для описания прямых в трехмерном пространстве. Уравнение прямой дает информацию, принадлежит ли точка с заданными координатами определенной прямой или нет. Рассмотрим два способа вывода этого уравнения. В первом случае выберем в пространстве две точк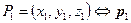и и .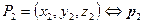

Проведем от точки 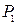к точке 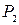обычный вектор равный разности векторов 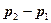. Этому вектору соответствует параллельный ему радиус-вектор 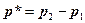, как показано на рис. 4. Тогда радиус-вектор 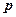, определяющий некоторую точку на прямой, можно получить сложением, например, вектора 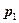и вектора 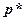, умноженного на некоторое число :

.

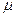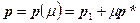Так мы получили уравнение прямой в векторной форме, с помощью, так называемых, базового и направляющего векторов, 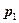и 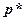, соответственно. Преобразуем это уравнение к виду, в котором используются только координаты двух исходных векторов.

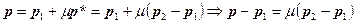(1)

Из этого векторного равенства получаем три равенства для соответствующих координат:

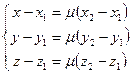
Попарно разделив эти уравнения друг на друга, получаем следующую систему уравнений, определяющую нашу прямую в трехмерном пространстве в форме записи через координаты точек:

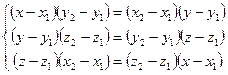(2)

В практических задачах иногда бывает нужно узнать, лежит ли некоторая точка, принадлежащая прямой, внутри отрезка, заданного координатами своих концов, на данной прямой или снаружи. Для решения этой задачи перепишем уравнение (1) в следующем виде:

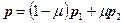(3)

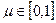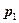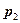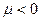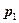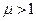При получаем точки прямой, лежащие между и . При – точки лежащие на прямой за , при – точки, лежащие на прямой за 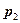. Для проверки этого просто подставьте в уравнение вместо 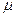значения 0 и 1.

Перейдем теперь к задаче вывода уравнения плоскости. Мы рассмотрим три способа его получения. Для этого прежде напомним определение скалярного произведения.
Для двух радиус-векторов 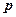и 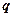скалярным произведением называется число 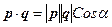, где 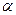– угол между векторам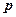и и 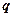. Для векторов запись вида 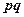или 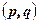также считается скалярным произведением. С практической точки зрения это определение может вызвать некоторое смущение. Действительно, вычислить угол между векторами, которые заданы координатами в трехмерном пространстве, вряд ли может показаться простым делом. Но, во-первых, часто бывает достаточно знать не само значение угла, а значение его косинуса, а во-вторых, скалярное произведение в ортонормированной системе координат можно выразить через координаты векторов:

,

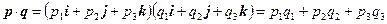так как при раскрытии скобок скалярные произведения перпендикулярных векторов базиса, по определению скалярного произведения, обращаются в ноль.

Уравнение плоскости

Используем свойства скалярного произведения для получения уравнения плоскости. Рассмотрим некоторую плоскость в пространстве и некоторую точку , про которую известно, что она лежит в этой плоскости, как показано на рисунке 5.

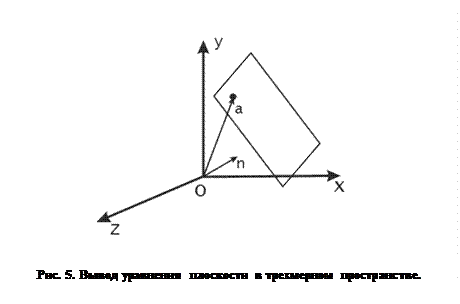Возьмем также некоторый радиус-вектор 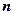, перпендикулярный нашей плоскости. Этот вектор назовем нормалью к плоскости. Пусть теперь требуется определить, принадлежит ли некоторая точка (или радиус-вектор) 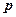плоскости или нет. Для этого заметим, что для любой точки 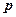, принадлежащей плоскости, вектор 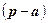и радиус-вектор нормали 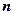– перпендикулярны. А это значит, что их скалярное произведение равно нулю:

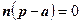(4)

Так, равенство (4) уже представляет собой уравнение плоскости в векторной форме. Раскрыв скобки, можно записать его в более удобном виде: 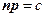, где константа 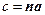. Если 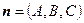, а 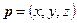, то в координатной записи уравнение плоскости запишется в виде

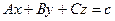(5)

Рассмотрим далее второй способ получения уравнения плоскости, которая задана тремя неколлинеарными векторами, или тремя, не лежащими на одной прямой, точками. Для этого рассмотрим определение операции векторного произведения. Результатом векторного произведения двух векторов 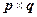является вектор 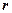, модуль которого равен 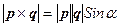, и направлен он перпендикулярно плоскости, в которой лежат векторы 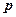и 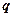, причем векторы 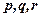– образуют правую тройку векторов (см. определение правой системы координат), здесь 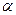– угол между векторам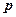и и 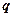. Для векторов единичного базиса, образующих правую тройку, как следует из определения: 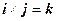, , 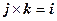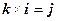. Векторное произведение так же подчиняется дистрибутивному закону, как и скалярное произведение. Однако векторное произведение не коммутативно, а именно, если для векторов 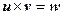, то 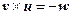, что также прямо следует из его определения. Координаты векторного произведения можно получить, если разложить векторы, участвующие в произведении, по базису, а затем раскрыть скобки, подобно тому, как это уже было проделано для скалярного произведения. Есть и другой, неформальный, но легче запоминаемый способ получения координат векторного произведения, с помощью разложения следующего определителя по его первой строке. Есл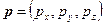и и 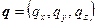, тогда

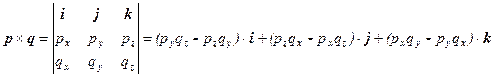
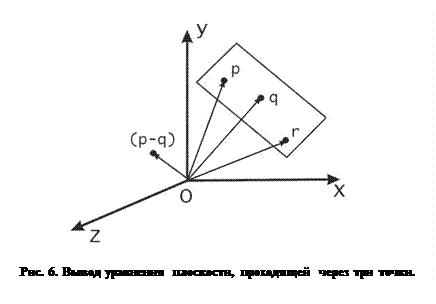
Сведем теперь условия в новой постановке задачи нахождения уравнения плоскости к предыдущему случаю, где мы использовали вектор нормали. Пусть заданы фиксированные векторы , и , не лежащие на одной прямой, определяющие плоскость, уравнение которой требуется получить (рис. 6).

Результат векторного произведения любых двух неколлинеарных векторов, параллельных нашей плоскости, будет вектором, перпендикулярным плоскости. И как раз такими являются векторы разност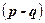и и 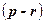. Выберем их векторное произведение в качестве вектора нормали, то есть 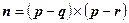. Тогда, если 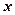– произвольный радиус-вектор, принадлежащий плоскости, то искомым уравнением плоскости будет, аналогично формуле (4):

,

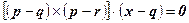причем уравнение этой же плоскости можно было бы записать, если в последней скобке вместо вектора 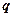использовать векторы 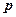или 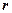. Не будем далее расписывать это уравнение через координаты, так как это не трудно проделать самостоятельно.

Рассмотрим еще несколько определений и типичных задач, решение которых не должно вызывать затруднений при решении более сложных задач.