Стационарные процессы в линии передачи

Цель работы — освоить основные понятия, физическую сущность и методы анализа процессов в цепи с распределенными параметрами (линии передачи).

Изучаются следующиеосновные вопросы:

1) понятия линии передачи, регулярной линии передачи; 2) основные параметры линии — погонные параметры, волновое сопротивление, коэффициент распространения, коэффициент фазы, коэффициент ослабления; 3) метод анализа процессов в регулярной линии при воздействии на нее гармонических колебаний; 4) характеристики бегущих волн в линии — фазовая скорость, длина волны, ослабление; 5) режимы работы линии — режимы бегущей волны, стоячей волны, смешанный; 6) параметры, характеризующие режим работы линии — коэффициент отражения, положение узлов и пучностей, коэффициент бегущей волны и коэффициент стоячей волны.

Домашнее задание

Изучите вышеперечисленные основные вопросы. Рекомендуются учебные пособия [1] (глава 10), [2] и конспект лекций.

1. Выпишите формулы, позволяющие, зная погонные параметры и частоту w, рассчитать волновое сопротивление R_в линии и основные характеристики волн в линии — коэффициент фазы b, фазовую скорость v_ф, длину волны в линии l.

2. Выпишите формулы, позволяющие, зная R_в, l и сопротивление нагрузки Z_н, рассчитать параметры, характеризующие режим работы линии — коэффициент отражения от нагрузки r_н, положение пучностей напряжения l₀, коэффициент бегущей волны k_бег и коэффициент стоячей волны k_ст.

3. Изобразите качественно (на двух графиках, см. ниже) характер кривых распределения амплитуды напряжения вдоль линии U(z):

· в режиме бегущей волны, т.е. для согласованной линии (R_н=R_в);

· в режиме стоячей волны — для разомкнутой линии (Z_н=¥), для короткозамкнутой линии (Z_н=0), для линии с реактивной нагрузкой (Z_н=jX_н, где X_н>0 и X_н<0);

· в смешанном режиме — для линии с резистивной нагрузкой (Z_н=R_н, где R_н>R_в и R_н<R_в), для линии с комплексной нагрузкой (Z_н=R_н+jX_н, где R_н>R_в или R_н<R_в, X_н>0 или X_н<0 — на ваш выбор).

Кривые для режимов бегущей и стоячей волны постройте на одном графике, кривые для смешанного режима — на другом. Расстояние от нагрузки z откладывайте «влево». На графиках укажите характерные значения амплитуды (U_пад и 2U_пад) и расстояния от нагрузки (λ/4 и λ/2).

Лабораторное задание

Данная работа выполняется на базе специального лабораторного блока, содержащего так называемый цепочечный эквивалент линии. Цепочечный эквивалент представляет собой цепь в виде каскадного соединения 20 одинаковых ячеек — LC-фильтров нижних частот. Длина одной ячейки l_яч=2,5 см, длина линии l_лин=50 см. Погонные реактивные параметры эквивалента линии известны: L₁=L_яч/l_яч, C₁=C_яч/l_яч, где L_яч и C_яч— указанные на блоке параметры одной ячейки.

Подготовка установки к работе

Подключите к эквиваленту линии генераторно-измерительную систему: генераторный выход системы — к входу линии (соединенному с зажимами «20—земля»), а измерительный вход системы — к зажимам «вольтметр» (соединенным со «щупом» линии). К выходу линии (соединенному с зажимами «0—земля») подключите переменный резистор.

Включите генераторно-измерительную систему (ее ярлык — на рабочем столе) и подготовьте ее к измерениям:

· установите режим изучения характеристик (осциллограмм) сигналов;

· оставьте отображение только расчетного входного сигнала и сформируйте сигнал в виде последовательности треугольных импульсов:

стационарные процессы в линии передачи - student2.ru

где u₀ = 0, U_И = 1 В, Т_И = 100 мкс, t₀ =0,период 1 мс;

· включите отображение генерируемого сигнала. Проверьте, что реальное входное напряжение действительно соответствует заданному. Если это не так, то выполните сервисную программу «калибровка». После этого отображение расчетного входного сигнала отключите;

· включите отображение измеряемого сигнала. Наблюдайте реальные входной и выходной сигналы.

1. Согласование линии с нагрузкой

Подберите к исследуемой линии согласованную нагрузку. Для этого подберите сопротивление R_нпеременного резистора нагрузки таким, чтобы напряжение на нагрузке повторяло напряжение генератора с минимальными искажениями и с минимальным изменением амплитуды. При этом можно считать, что к линии подключена согласованная нагрузка, т.е. R_н=R_в.

После этого замените переменный резистор нагрузки (не изменяя подобранного положения регулятора!) имеющейся согласованной нагрузкой. Убедитесь, что эта нагрузка действительно обеспечивает согласование линии.

2. Измерение основных параметров волны в линии

Экспериментально определите волновое сопротивление линии, для чего с помощью омметра измерьте подобранное сопротивление переменного резистора нагрузки R_н=R_в. Измеренное таким образом значение R_в внесите в таблицу и сравните с расчетным (рассчитанным по известным погонным параметрам линии).

Образец таблицы

R_в, Ом	v_ф, м/с	Примечание

		Измерение
		Расчет

Экспериментально определите скорость распространения волны в линии. Для этого с помощью курсоров измерьте запаздывание Dt импульса на согласованной нагрузке по сравнению с импульсом генератора, а по этому запаздыванию определите фазовую скорость v_ф=l_лин/Dt. Измеренное таким образом значение v_ф внесите в ту же таблицу и сравните с расчетным (рассчитанным по известным погонным параметрам линии).

3. Режим бегущей волны

Перейдите в режим гармонических колебаний, для чего сформируйте гармоническое напряжение с заданной частотой f (см. таблицу заданий) и скорректируйте амплитуду генерируемого напряжения (так, чтобы амплитуда напряжения на согласованной нагрузке U_н= 1 В).

Изучите распределение амплитуды и фазы напряжения вдоль согласованной линии. Для этого, перемещая «щуп» от нагрузки к генератору, с помощью курсоров измерьте распределения амплитуды U(z) и фазы j(z), где

стационарные процессы в линии передачи - student2.ru (град) ,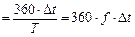

и постройте их графики (требуемые пределы напряжения — от 0 до 2 В, рекомендуемый масштаб — 200 мВ в 1 см, расстояние от нагрузки z откладывайте «влево»). По графику j(z) определите коэффициент фазы b, внесите его в таблицу и сравните с расчетным.

Образец таблицы

f, кгц	Нагрузка	b, 1/м	l, см	Примечание
	Соглас.		—	Измерение
Хх	—
Кз	—
—			Расчет
	Соглас.		—	Измерение
—			Расчет

Повторите изучение распределения фазы напряжения вдоль согласованной линии и измерение коэффициента фазы для другой частоты (примерно на 30% большей или меньшей — на ваш выбор). Новое распределение фазы нанесите на ранее построенный график, новое значение коэффициента фазы внесите в ту же таблицу и сравните с расчетным.

После этого вновь установите исходную (заданную) частоту гармонического напряжения.

4. Согласование линии с генератором

В последующих пунктах изучаются распределения амплитуды и фазы напряжения вдоль линии при различных сопротивлениях нагрузки. Для наглядности сравнения результатов все измерения целесообразно проводить при одной и той же амплитуде падающей волны. Это осуществляется в режиме согласования линии с генератором.

Для согласования линии с генератором отключите согласованную нагрузку от выхода линии и подключите ее к входу линии (последовательно с генератором, т.е. между гнездами «выход» генератора и «20» линии). Установите амплитуду генерируемого напряжения U_ген= 2 В (при согласовании линии с генератором U_пад= U_ген/2 = 1 В).

5. Режим стоячей волны

Изучите распределение амплитуды напряжения вдоль разомкнутой линии. Для этого при отключенной нагрузке (R_н=¥) снимите кривую распределения амплитуды U(z) и нанесите ее на ранее построенный график. При этом обратите внимание на распределение фазы напряжения в линии. По измеренной кривой определите длину волны в линии l, внесите ее в ту же таблицу и сравните с расчетной.

Изучите распределение амплитуды напряжения вдоль короткозамкнутой линии. Для этого подключите к выходу линии короткозамыкатель (R_н=0), снимите кривую распределения амплитуды U(z) и нанесите ее на тот же график. По построенной кривой также определите длину волны в линии l, внесите ее в ту же таблицу и сравните с расчетной и с измеренной в разомкнутой линии.

6. Изучение смешанного режима

Изучите распределение амплитуды напряжения вдоль линии с резистивной нагрузкой. Для этого подключите к выходу линии заданный резистор (R_н≠R_в), снимите кривую распределения амплитуды U(z) и нанесите ее на тот же график. По построенной кривой определите сопротивление нагрузки и сравните его с известным номинальным сопротивлением резистора.

Изучите распределение амплитуды напряжения вдоль линии с комплексной нагрузкой. Для этого подключите к выходу линии комплексную нагрузку, снимите и постройте (на отдельном графике) кривую распределения амплитуды U(z).

Контрольные вопросы

1. Что такое волновое сопротивление линии? Какой физический смысл имеет этот параметр?

2. Что такое коэффициент распространения? коэффициент фазы? коэффициент ослабления? Какой физический смысл имеют эти параметры? Как можно измерить коэффициент фазы?

3. Что такое фазовая скорость? длина волны в линии? Какой физический смысл имеют эти величины? Как можно их измерить?

4. Изобразите характер распределения амплитуды напряжения вдоль линии, нагруженной на резистор (R_н=R_в, R_н>R_в, R_н<R_в).

5. Изобразите характер распределения амплитуд напряжения и тока вдоль линии, к выходу которой подключен конденсатор. Как изменится это распределение, если емкость конденсатора увеличить? если конденсатор отключить?

6. Изобразите характер распределения амплитуд напряжения и тока вдоль линии, к выходу которой подключена индуктивная катушка. Как изменится это распределение, если индуктивность катушки уменьшить? если катушку отключить?

7. Что такое коэффициент отражения от нагрузки? Чему равны его значения при согласованной нагрузке? при холостом ходе? при коротком замыкании?

8. Что такое коэффициент бегущей волны? коэффициент стоячей волны? Как измерить эти коэффициенты? Чему равны их значения при согласованной нагрузке? при холостом ходе? при коротком замыкании?

9. Изобразите характер распределения амплитуды напряжения вдоль линии без потерь, работающей в режиме «полного отражения» от нагрузки (|ρ_н|=1, п. 5). Как изменится это распределение, если в линии есть потери?

_____________

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Баскаков С.И. Лекции по теории цепей. – М.: Эдиториал УРСС, 2001. – 280 с.

2. Попов В.П. Основы теории цепей. – М.: Высшая школа, 2000.– 575 с.

3. Гречихин В.А. Основы теории цепей: Руководство к решению задач анализа линейных цепей с сосредоточенными параметрами. – М.: Издательство МЭИ, 2002.– 92 с.

4. Компьютерная генераторно-измерительная система для изучения электрических цепей и сигналов / Б.П. Поллак, Л.И. Пейч, Д.А. Точилин и др. // Вестник МЭИ. – 2003. №4. С. 92–99.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ
Многофункциональная лабораторная установка для изучения радиотехнических цепей и сигналов . . . . . . . . . .
Лабораторный стенд «Сигнал-1» . . . . . . . . . . . . .
Компьютерная генераторно-измерительная система. . . . .
Правила выполнения лабораторных работ в лаборатории ОТЦ.
ЛАБОРАТОРНЫЕ РАБОТЫ. . . . . . . . . . . . . . . .
Лабораторная работа № 10 Переходные процессы в апериодических и колебательных цепях . . . . . . . . . . . . . . . . . . . . . . .
Лабораторная работа № 11 Апериодические и колебательные цепи при импульсных воздействиях . . . . . . . . . . . . . . . . . . . . . .
Лабораторная работа № 13 Резистивная цепь с нелинейным двухполюсником . . . . .
Лабораторная работа № 14 Стационарные процессы в линии передачи . . . . . . . .
БИБЛИОГРАФИЧЕСКИЙ СПИСОК . . . . . . . . . . . .