Стационарные случайные процессы

Случайная функция X(t)называется строго стационарной (стационарной в узком смысле), если ее n-мерные законы распределения инвариантны относительно сдвига во времени на величину t.

Если случайная функция строго стационарна, то ее математическое ожидание и дисперсия постоянны, т.е. не зависят от времени, а корреляционная функция зависит только от разности моментов времени, т.е. от t. Обратное утверждение в общем случае неверно. Случайный процесс X(t)называется стационарным в широком смысле, если его математическое ожидание и дисперсия постоянны, а корреляционная функция зависит только от разности аргументов:

m_x = const , D_x =const , K_x(t₁,t₂) = K_x(t₂ - t₁).

Корреляционная функция стационарной в широком смысле случайной функции обозначается 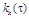и обладает следующими свойствами:

1) k_x(-t) = k_x(t);

2) | k_x(t)| £ D_x;

Если X(t) – стационарная в широком смысле дифференцируемая функция и 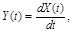то Y(t) – также стационарная в широком смысле случайная функция, причем

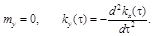(9.6)

Для дифференцируемости стационарной в широком смысле случайной функции необходимо и достаточно существование второй производной корреляционной функции при t = 0.

Важнейшим свойством стационарных процессов является свойство эргодичности, когда средняя случайного процесса по множеству реализаций равна средней по одной реализации на бесконечном промежутке времени.

Средней по реализации на конечном промежутке времени [0,T] называется число, определяемое выражением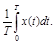

Стационарный случайный процесс называется эргодическим относительно математического ожидания, если

.

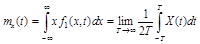Стационарный случайный процесс называется эргодическим относительно корреляционной функции, если

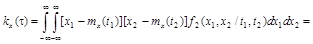
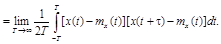
Стационарный в широком смысле случайный процесс, заданный каноническим разложением вида

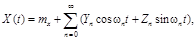(9.7)

где 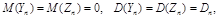называется случайным процессом с дискретным спектром. Корреляционная функция такого процесса имеет вид

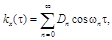
а дисперсия равна сумме дисперсий отдельных гармоник на частотах

: .

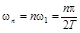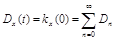Стационарный случайный процесс называется случайным процессом с непрерывным спектром, если существует такая действительная неотрицательная функция S_x(w), определенная при всех wÎR и называемая спектральной плотностью, что

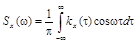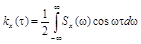; . (9.8)

Как видно, корреляционная функция и спектральная плотность стационарного процесса с непрерывным спектром связаны между собой взаимно обратными косинус-преобразованиями Фурье. В комплексной форме они имеют вид:

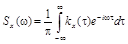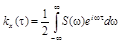, . (9.9)

Дисперсия такого процесса равна

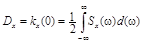. (9.10)

Условия неотрицательности 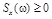и четности 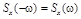являются необходимыми условиями стационарности в широком смысле случайного процесса X(t).

Нормированной спектральной плотностью называется отношение спектральной плотности к дисперсии процесса:

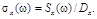(9.11)

Стационарная случайная функция с постоянной спектральной плотностью называется стационарным белым шумом. Нормированная спектральная плотность стационарного белого шума со спектром частот 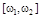имеет вид

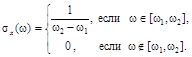
Если X(t) – стационарный в широком смысле процесс с спектральной плотностью

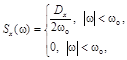
то он называется низкочастотным белым шумом.

Выясним, является ли низкочастотный белый шум дифференцируемым. Найдём корреляционную функцию этого процесса.

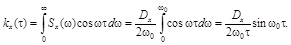
Её первая и вторая производные соответственно равны:

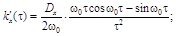
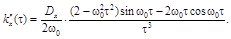
Вычислим модуль второй производной при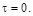

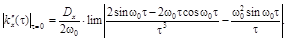
Применяя к первой дроби правило Лопиталя и переходя к пределу, получим:

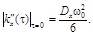
Так как 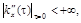то процесс дифференцируем.

На практике часто используются такие характеристики стационарного процесса, как эффективная ширина спектра 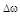и средний интервал корреляции (эффективная длительность корреляционной функции) 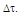Они находятся по формулам:

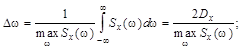(9.12)

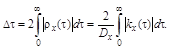(9.13)

Геометрически эффективная ширина спектра 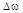равна основанию прямоугольника с высотой 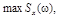площадь которого равна площади фигуры под криво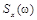й при 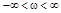, а средний интервал корреляции 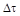равен основанию прямоугольника с высотой 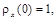площадь которого равна площади фигуры под криво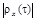й при .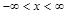

Справедливо так называемое соотношение неопределённости 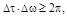смысл которого заключается в следующем: чем уже ширина спектра стационарного процесса, тем больше интервал корреляции его сечений, и наоборот.

9.35.Корреляционная функция случайного процесса X(t) имеет вид 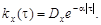Найти спектральную плотность, эффективную ширину спектра 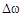и средний интервал корреляции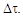

¢ Найдём спектральную плотность:

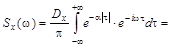
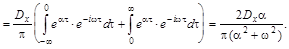
Нетрудно видеть, что 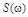- чётная функция с единственной точкой максимума при .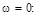

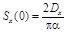Эффективная ширина спектра в данном случае равна 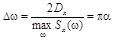, средний интервал корреляции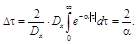

Как видно, 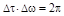- соотношение неопределённости обращается в равенство. £

9.36.На вход дифференцирующего устройства поступает случайный процесс с математическим ожиданием 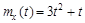и корреляционной функцией 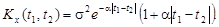. Дифференцируем ли данный процесс в среднеквадратичном?

9.37.Задана корреляционная функция 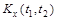случайного процесса X(t). Показать, что взаимная корреляционная функция случайных процессов X(t) и 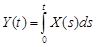может быть представлена в виде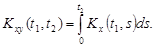

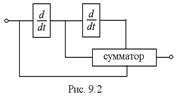
9.38.На вход радиотехнической цепи, состоящей из последовательно соединённых дифференцирующих устройств и сумматора, поступает случайный стационарный сигнал X(t) c 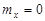и корреляционной функцией 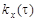(рис.9.2). Найти .

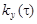9.39.Является ли эргодической по отношению к математическому ожиданию синусоидальная стационарная случайная функция определённой частоты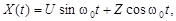

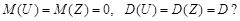
9.40.Является ли эргодическим относительно корреляционной функции случайное гармоническое колебание 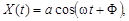где a - постоянная амплитуда, а 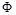- равномерно распределённая на отрезке 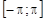случайная величина?

9.41.Случайный процесс задан следующим образом: 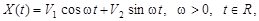где 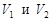- независимые случайные величины, принимающие с равной вероятностью лишь два возможных значения +I и -I. Найти корреляционную функцию процесса и убедиться, что 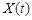стационарен в широком смысле, но не является стационарным в узком смысле.

9.42.Установить, дифференцируем ли стационарный случайный процесс, корреляционная функция которого имеет вид

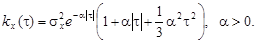
9.43.Показать, что взаимная корреляционная функция 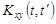стационарной случайной функции X(t) и её производной 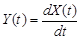удовлетворяет условию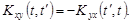

9.44.Показать, что если стационарный случайный процесс X(t) дифференцируем, то он стационарно связан со своей производной. Найти 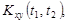где .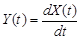

9.45.Пусть X(t) - произвольный случайный процесс, стационарный в широком смысле. Доказать «соотношение неопределённости». См. задачу 9.35.

9.46 – 9.50. Дана корреляционная функция стационарного случайного процесса. Найти его спектральную плотность.

9.46.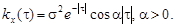

9.47.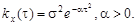

9.48.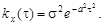

9.49.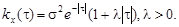

9.50.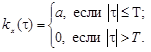

9.51 – 9.54. Дана спектральная плотность стационарного случайного процесса. Найти его корреляционную функцию.