Передача параметров в потоке кода

В этом необычном методе передаваемые процедуре данные размещаются прямо в коде программы, сразу после команды CALL (как реализована процедура print в одной из стандартных библиотек процедур для ассемблера UCRLIB):

call print

db "This ASCIZ-line will be printed",0

(следующая команда)

Чтобы прочитать параметр, процедура должна использовать его адрес, который автоматически передается в стеке как адрес возврата из процедуры. Разумеется, функция должна будет изменить адрес возврата на первый байт после конца переданных параметров перед выполнением команды RET. Например, процедуру print можно реализовать следующим образом:

print proc near

push bp

mov bp,sp

push ax

push si

mov si,[bp+2] ; прочитать адрес

; возврата/начала данных

cld ; установить флаг направления

; для команды lodsb

print_readchar:

lodsb ; прочитать байт из строки,

test al,al ; если это 0 (конец строки),

jz print_done ; вывод строки закончен

int 29h ; вывести символ в AL на экран

jmp short print_readchar

print_done:

mov [bp+2],si ; поместить новый адрес возврата в стек

pop si

pop ax

pop bp

ret

print endp

Передача параметров в потоке кода, так же, как и передача параметров в стеке в обратном порядке (справа налево), позволяет передавать различное число параметров. Но этот метод - единственный, позволяющий передать по значению параметр различной длины, что и продемонстрировал этот пример. Доступ к параметрам, переданным в потоке кода, несколько медленнее, чем к параметрам, переданным в регистрах, глобальных переменных или стеке, и примерно совпадает со следующим методом.

Задания

Дан двумерный массив. Размер массива и его элементы вводятся пользователем с клавиатуры. Результат работы программы выводится на экран. Необходимы алгоритмы обработки массива оформить виде процедур, такие как ввод элементов массива, вывод массива на экран, поиск минимального элемента, поиск максимального элемента и т.п.

Варианты:

Вариант 1

Из исходного массива двузначных десятичных чисел со знаком получить два новых, поместив в первый из них значения элементов, превосходящих среднее значение массива, а во второй номера этих элементов (среднее = ).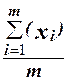

Вариант 2

Из двух исходных массивов двузначных десятичных чисел без знака X и Y cформировать массив Z, поместив в него все элементы исходных, превышающие общее среднее = .

Вариант 3

Из исходного массива двузначных десятичных чисел со знаком получить два новых, поместив в первый из них номера максимальных, а во 2-ой номера минимальных элементов исходного. (Предполагается, что MIN и MAX могут быть не единственными).

Вариант 4

Найдите в массиве двузначных десятичных чисел без знака X все элементы 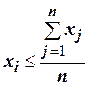и их номера и поместите эти значения в два новых массива Y - элементов и Z - индексов.

Вариант 5

Из исходного массива X двузначных десятичных чисел со знаком сформировать массив Y- отклонений от среднего
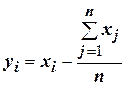( ) и массив Z- номеров элементов исходного массива, превышающих среднее.

Вариант 6

Выявить все номера элементов массива двузначных десятичных чисел без знака X, превышающих (max+min)/2. В результате сформировать 2 массива: Y- масив номеров и Z- массив значений, для которых выполняется заданное условие.

Вариант 7

Из исходного массива двузначных десятичных чисел со знаком X получить новый массив Y ( ).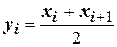

Подсчитайте среднее = .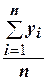

Вариант 8

Из исходного массива двузначных десятичных чисел без знака получить два новых, поместив в них значения и номера элементов, для которых выполняется условие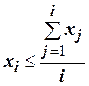

Вариант 9

Из исходного массива двузначных десятичных чисел со знаком X получить два новых Y и Z, таких что:

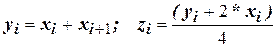
Вариант 10

Получить из исходного массива X двузначных десятичных чисел без знака два новых Y, Z, поместив в них элементы и номера элементов массива X, для которых выполняется условие .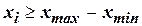

Вариант 11

Получить из исходного массива X двузначных десятичных чисел без знака два новых Y, Z, помеcтив в них номера элементов и их значения, для которых выполняется условие .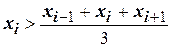

Вариант 12

Получить из исходного массива X двузначных десятичных чисел со знаком два новых Y, Z, поместив в них элементы и номера, для которых выполняется условие .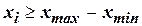

Вариант 13

Из исходного массива X двузначных десятичных чисел без знака получить два новых Y, Z, поместив в Y элементы, значения которых меньше (X_max+X_min)/ 2, а в Z - номера этих элементов.

Вариант 14

Из исходного массива X двузначных десятичных чисел со знаком получить два новых Y, Z, поместив в первый из них нечетные значения элементов массива, а во второй – их номера.

Вариант 15

Из исходного X двузначных десятичных чисел без знака получить два новых Y, Z, поместив в первый из них номера элементов превышающих заданное число А, а во второй - элементы, значения которых меньше среднего в массиве (среднее = ).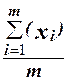

Вариант 16

Получить из исходного массива X двузначных десятичных чисел без знака два новых Y, Z, поместив в них элементы и номера, для которых выполняется условие x _i <= x_i-1 + x_i+1.

Вариант 17

Из исходного массива двузначных десятичных чисел без знака X получить два новых Y и Z, таких что:

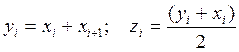
Вариант 18

Получить из исходного массива X двузначных десятичных чисел со знаком два новых Y, Z, поместив в них элементы и номера элементов массива X, для которых выполняется условие: x_i <= x_max – x_min.

Вариант 19

Получить из исходного массива X двузначных десятичных чисел со знаком два новых Y, Z, поместив в них номера элементов и их значения, для которых выполняется условие: x_i < (x_i-1 +x_i +x_i+1)/3.

Вариант 20

Получить из исходного массива X двузначных десятичных чисел без знака два новых Y, Z, поместив в них элементы и номера, для которых выполняется условие: x_i <= x_max +x_min.

Вариант 21

Из исходного массива X двузначных десятичных чисел со знаком получить два новых Y, Z, поместив в Y элементы, значения которых меньше (x_max-x_min)/ 4, а в Z - номера этих элементов.

Вариант 22

Из исходного массива X двузначных десятичных чисел без знака получить два новых Y, Z, поместив в первый из них четные значения элементов массива, а во второй – их номера.

Вариант 23

Из исходного X двузначных десятичных чисел со знаком получить два новых Y, Z,, поместив в первый из них номера элементов не превышающих заданное число А, а во второй - элементы, значения которых больше среднего в массиве (среднее = ).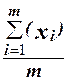

Вариант 24

Получить из исходного массива X двузначных десятичных чисел со знаком два новых Y, Z, поместив в них элементы и номера, для которых выполняется условие x _i = x_i-1 + x_i+1.

Вариант 25

Из исходного массива двузначных десятичных чисел без знака получить два новых, поместив в первый из них значения элементов, не превосходящих среднее значение массива, а во второй номера этих элементов (среднее = ).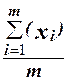

Вариант 26

Из двух исходных массивов двузначных десятичных чисел со знаком X и Y cформировать массив Z, поместив в него все элементы исходных, не превышающие общее среднее = .

Вариант 27

Из исходного массива двузначных десятичных чисел со знаком X сформировать массив Z, поместив в него только те элементы, которые не превышают разность максимального и минимального элементов массива.

Вариант 28

Из исходного массива двузначных десятичных чисел со знаком X сформировать массив Z, в котором нечетные элементы исходного массива Х заменены на сумму номеров минимального и максимального элементов.

Вариант 29

Получить из исходного массива X двузначных десятичных чисел со знаком два новых Y, Z, поместив в них элементы и номера элементов массива X, для которых выполняется условие: x_i <= последнего отрицательного элемента.

Вариант 30

Получить из исходного массива X двузначных десятичных чисел со знаком два новых Y, Z, поместив в них элементы и номера элементов массива X, для которых выполняется условие: x_i >= последнего нечетного элемента.

Вариант 31

Получить из исходного массива X двузначных десятичных чисел без знака, два новых Y, Z, поместив в них элементы и номера элементов массива X, для которых выполняется условие: x_i <=максимального среди четных элементов.

Вариант 32

Получить из исходного массива X двузначных десятичных чисел без знака, два новых Y, Z, поместив в них элементы и номера элементов массива X, для которых выполняется условие: x_i >=минимального среди нечетных элементов.

Вариант 33

Получить из исходного массива X двузначных десятичных чисел без знака, два новых Y, Z, поместив в них элементы и номера элементов массива X, для которых выполняется условие: x_i >минимального среди кратных 3 элементов.

Вариант 34

Получить из исходного массива X двузначных десятичных чисел со знаком, два новых Y, Z, поместив в них элементы и номера элементов массива X, для которых выполняется условие: x_i <максимального среди кратных 3 элементов.

Вариант 35

Из исходного X двузначных десятичных чисел без знака получить два новых Y, Z, поместив в первый из них номера элементов превышающих введенного с клавиатуры числа А, а во второй - элементы, значения которых больше разности максимального элемента и числа A.

Вариант 36

Из исходного X двузначных десятичных чисел без знака получить два новых Y, Z, поместив в первый из них номера элементов меньше количества нулевых элементов, а во второй - элементы, значения которых больше количества не нулевых элементов.

Вариант 37

Из исходного X двузначных десятичных чисел без знака получить два новых Y, Z, поместив в первый из них номера элементов меньше разности последнего четного и первого нечетного элементов, а во второй их значения.

Вариант 38

Из исходного X двузначных десятичных чисел без знака получить два новых Y, Z, поместив в первый из них значения элементов больше половины суммы последнего четного и минимального элементов, а во второй их номера.

Вариант 39

Из исходного X двузначных десятичных чисел без знака получить два новых Y, Z, поместив в первый из них значения элементов меньше суммы первого четного, последнего нечетного, минимального и максимального элементов, деленных на четыре, а во второй их номера.

Вариант 40

Из исходного X двузначных десятичных чисел без знака получить два новых Y, Z, поместив в первый из них значения элементов больше разности минимального плюс максимального элементов и количества нулевых элементов, деленных на четыре, а во второй их номера.

Список литературы:

1) Питер Абель Assembler и программирование для IBM PC 1995.

2) Юров В. Assembler, 2001

3) Зубков С.В. Assembler. Язык неограниченных возможностей. 1999.

4) Пильщиков В.Н. Программирование на языке ассемблера IBM PC. 1997.

5) Орлов С.Б. Программа-справочник по системе программирования турбо ассемблер 2.0. Руководство пользователя. М. 1990г.