Вычисление определенного интеграла с заданной точностью

Задача вычисления определенного интеграла формулируется следующим образом: вычислить I= 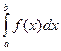c точностью ε при известных значения пределов интегрирования a, b, известной точности ε и заданной подынтегральной функции f(x). При вычислении интеграла с точностью будут использоваться изложенные ранее методы прямоугольников, трапеций и парабол для вычисления интеграла при заданном числе разбиений интервала интегрирования. Для оценки погрешности вычисления интеграла на практике используют правило [6]. Суть правила состоит в том, что выполняют вычисление интеграла с двумя разными шагами изменения переменной x, а затем сравнивают результаты вычислений и получают оценку точности. Наиболее часто используемое правило связано с вычислением интеграла дважды: с шагом h и шагом h/2.

Для методов прямоугольников и трапеций погрешность R_h/2 вычисления интеграла с шагом h/2 оценивается следующей формулой:

|R_h/2 | = ,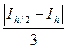

где I_h/2 – значение интеграла, вычисленное с шагом h/2;

I_h – значение интеграла, вычисленное с шагом h.

Для метода Симпсона погрешность оценивается в соответствии со следующим выражением:

|R_h/2 | = .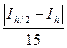

Шаг интегрирования для методов прямоугольников и трапеций пропорционален величине 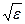, поэтому в [6] рекомендовано начальное количество разбиений выбирать согласно следующему выражению n=] 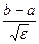[ + 1, где ][ - целая часть. Для метода парабол шаг интегрирования пропорционален величине 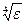, поэтому начальное количество шагов рекомендовано выбирать из следующего выражения n=] 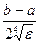[ + 1.

В программе вычисления интеграла с точностью во внутреннем цикле вычисляется значение определенного интеграла при заданном (фиксированном) числе разбиений интервала интегрирования. Во внешнем цикле производится сравнение значений интегралов, вычисленных при числе шагов, равных n и 2n соответственно. Если требуемая точность не достигнута, то производится удвоение числа разбиений, а в качестве предыдущего значения интеграла берется текущее; процесс вычисления интеграла выполняется при новом числе разбиений.

В дальнейшем в программах при вычислении значений аргумента используется формула арифметической прогрессии X=X_н +(i-1)*dx, а не формула накопления суммы X=X+dx, так как в первом случае получается меньшая погрешность вычислений [7].

Пример программы вычисления определенного интеграла 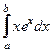( 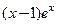- первообразная подынтегральной функции) с точностью ε методом трапеций.

program integraltrap;

{$APPTYPE CONSOLE}

uses SysUtils, Math;

function Rus(S:String):String;

var I:Byte;

begin

Result:='';

for I:=1 to Length(S) do

case S[I] of

'А'..'п': Result:=Result+Chr(Ord(S[I])-64);

'р'..'я': Result:=Result+Chr(Ord(S[I])-16);

'Ё': Result:=Result+Chr(240);

'ё': Result:=Result+Chr(241);

else

Result:=Result+S[I];

end;

end;

var

A,B,Eps,I1,I2,Itoch,X,Dx,S1:Real;

I,N,M,K:Integer;

begin

WriteLn(Rus('Введите пределы интегрирования и точность'));

ReadLn(A,B,Eps);

//вычисление начального количества разбиений

N:=Trunc((B-A)/Sqrt(Eps))+1;

//полусумма значений функции на нижнем и

//верхнем пределах интегрирования

S1:=(A*Exp(A) + B*Exp(B))/2.0;

//начальное значение интеграла, вычисленное

//при начальном количестве разбиений

Dx:=(B-A)/N;

I2:=0;

for I:=1 to N-1 do

begin

X:=A+I*Dx; // текущее значение аргумента

//вычисление суммы значений функции в узлах интегрирования

I2:=I2+X*Exp(X);

end;

I2:=(S1+I2)*Dx;

//вычисление количества позиций при выводе

//числа с заданной точностью

M:=Trunc(-Log10(Eps))+2;

K:=Trunc(Log10(Abs(I2)))+M+3;

Writeln(Rus('Начальное количество разбиений=')

,N:4,Rus(' Интеграл='),I2:K:M);

//цикл вычисления интеграла с точностью

repeat

//предыдущему значению интеграла присваивается текущее

I1:=I2;

//начальному значению суммы присваивается полусумма

//значений функции на концах интервала интегрирования

I2:=S1;

N:=N*2; //удвоение количества разбиений

Dx:=(B-A)/N; //шаг изменения переменной интегрирования

//внутренний цикл для вычисления суммы значений

//функции при фиксированном количестве шагов

for I:=1 to N-1 do

begin

X:=A+I*Dx; // текущее значение аргумента

//вычисление суммы значений функции в узлах интегрирования

I2:=I2+X*Exp(X);

end;

I2:=I2*Dx; //текущее значение интеграла

until Abs(I2-I1)/3<Eps; //анализ точности вычисление

WriteLn(Rus('Значение интеграла ='),I2:K:M

,Rus(' при количестве разбиений, равном '), N div 2);

Itoch:=(B-1)*Exp(B)-(A-1)*Exp(A);//точное значение интеграла

WriteLn(Rus('Точное значение интеграла равно '),Itoch:K:M);

ReadLn;

end.

Следует заметить, что метод трапеций удобен для вычисления интеграла по правилу Рунге, так как при увеличении количества разбиений в два раза каждый второй узел представляет собой ранее рассматривавшийся узел, поэтому вновь значения функции в этих точках вычислять не следует. Для этого следует сумму значений функции в этих узлах сохранять в переменной s2 .

Фрагмент модифицированной программы приведен ниже. В отличие от первого варианта программы до вложенного цикла необходимо написать цикл вычисления сумм значений функции при начальном разбиении интервала интегрирования для всех узлов, кроме первого и последнего.

ReadLn(A,B,Eps);

N:=Trunc((B-A)/Sqrt(Eps))+1;

S1:=(A*Exp(A) + B*Exp(B))/2.0;

S:=0;

Dx:=(B-A)/N;

//Цикл вычисления суммы значений функции в узлах интегриро-

//вания при начальном разбиении интервала интегрирования

for I:=1 to N-1 do

begin

X:=A+I*Dx;

S:=S+ X*Exp(X);

end;

I2:=Dx*(S+S1);

S2:=S;

repeat

I1:=I2;

N:=N*2;

Dx:=(B-A)/N;

X1:=A+Dx; //Координата первого нового узла интегрирования

S:=0;

//Цикл вычисления суммы значений функции

//в новых узлах интегрирования

for I:=1 to N div 2 do

begin

X:=X1+2*(I-1)*Dx;

S:=S+ X*Exp(X);

end;

//Сумма значений функции в узлах интегрирования

//при новом числе разбиений

S2:=S+S2;

I2:=(S1+S2)*Dx;

until Abs(I2-I1)/3<Eps;

Таким же образом можно сократить количество выполняемых операций при вычислении интеграла по методу левых или правых прямоугольников. Однако на практике при использовании метода прямоугольников значение функции вычисляют не на конце интервала (левом или правом), а в его середине. В этом случае при удвоении числа разбиений ранее вычисленные значения функции (и их сумму) использовать не удается. Для использования результатов ранее выполнявшихся вычислений при применении метода прямоугольников следует количество разбиений увеличивать в три раза и вычислять значения функции в точках с абсциссами X_i = X_нач +hi/6+h(i-1), i=1,n; X_j = X_нач +5hj/6+h(j-1), j=1,n. В приведенных выражениях X_нач – нижний предел интегрирования, h – шаг интегрирования и n – количество разбиений на предыдущей итерации.

При вычислении интеграла по методу Симпсона можно непосредственно использовать суммы значений функции, вычислявшиеся на предыдущей итерации. При этом надо иметь в виду, что узлы с нечетными номерами получают на очередной итерации четные индексы и сумма значений функции для этих узлов должна браться с коэффициентом 2 (на предыдущей итерации с коэффициентом 4). Узлы с четными номерами и при новой итерации останутся четными, поэтому сумма значений в этих узлах берется с тем же коэффициентом 2.