Обход списка и переход к узлу по номеру от головы списка
Обход списка осуществляется с целью анализа, обработки и поиска данных находящихся в списке. Заметим, что переход к следующему узлу осуществляется присваиванием указателю C на текущий узел значения указателя на следующий узел cur->next. Но по определению списка, последний узел в списке содержит пустой указатель на следующий узел. А значит это и является признаком конца обхода списка. Таким образом, стандартный алгоритм обхода списка прост:
3. Выполнять в цикле:
4. Обработать текущий узел.
5. Перейти к следующему узлу.
6. До тех пор пока указатель на следующий узел станет пустым.
Пример 34. Напишем процедуру обохода списока с целью вывода его содержимого на экран и поиска совпадающей строки, а также функцию перехода к узлу списка по номеру.
void PrintSearchList (list head, int val)
//Head – указатель на голову списка, str – искомая строка
{
bool lfound = false; // признак того, что строка найдена
tail = &head; //начинаем с головы списка
while (tail != NULL)// если указатель на текущий элемент списка не пуст
{
printf("%d\n", tail->value); //выводим информационное поле списка
if (tail->value = val) lfound = true; //совпадает с искомой строкой?
tail = tail->next; //переходим к следующему узлу списка
}
if (lfound) printf("Элемент в списке найден!");
else printf("Элемент в списке не найден!");
}
list GotoNode (list head, int cnt)
//Cnt – номер узла, начиная с 1, к которому нужно перейти
{
int i = 1;
tail = &head;
while ((tail->next != NULL) && (i < cnt))
{
i++;
tail = tail->next;
}
return(*tail);
}
Стек, очередь, дек
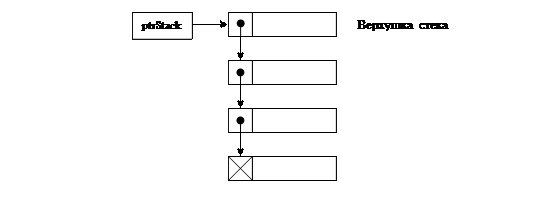
Стеком (англ. stack) называется хранилище данных, в котором можно работать только с одним элементом: тем, который был добавлен в стек последним. Говорят, что стек реализует дисциплину обслуживания LIFO (Last In – First Out, последним пришел – первым ушел). Физически стек может быть реализован на основе массива или на основе односвязанного линейного списка, в котором все операции осуществляются только с головой списка. Этот элемент в стеке называется верхушкой стека и на него указывает указатель стека ptrStack (рис.43). Если указатель стека – пустой, то стек считается пустым.
Стек должен поддерживать следующие операции:
push – добавить (положить) в верхушку стека новый элемент;
pop – извлечь из верхушки стека элемент;
isEmpty – проверка, пуст ли стек;
top – узнать (прочитать) значение верхушки стека (не удаляя ее);
size – узнать количество элементов в стеке;
clear – очистить стек (удалить из него все элементы).
|
Поскольку стек с точки зрения программной реализации является частным случаем односвязного линейного списка, то на языке Паскаль стек можно описать с помощью следующих структур:
struct st // объявление типа stack
{
char info; информационная часть
struct st *ps; // указатель на предыдущий (более нижний) элемент стека
} stack;
Стек имеет очень широкое применение в программировании. Особенно часто он используется при решении системных задач, задач компиляции и анализа выражений. Рассмотрим наиболее характерный пример использования стека при переводе выражений в обратную польскую запись.
Обратная польская запись (ОПЗ) – это способ записи выражений (как правило алгебраических) в так называемом постфиксном (или суффиксном) виде, т.е. в таком виде, когда сначала записываются все операнды, а потом выполняемые над ними операции, т.е. для обычных бинарных операций сложения, вычитания, умножения и деления знак операции располагается после операндов, а не между ними как в привычном «инфиксном» виде. Одна из особенностей ОПЗ – отсутствие скобок, что позволяет вычислять ОПЗ за один проход слева направо. ОПЗ как правило используется в трансляторах и компиляторах для преобразования выражений в машинный код, их последующего вычисления, а также для анализа и трансляции синтаксических конструкций языка к виду, удобному для генерации машинного кода.
Пример 35. Представим выражение (a+b)/(c/a*c – e*d) в постфиксном виде:
ОПЗ: ab+ca/c*ed*–/. Вычислим ОПЗ слева на право, при вычислении пользуемся правилом: «в операции участвуют два операнда, расположенные слева от знака операции».
1. Первое вычисление: R1 = ab+ = a+b, подставляем в исходную строку вместо ab+ вычисленный результат R1получается ОПЗ: R1ca/c*ed*–/.
2. Второе действие: R2 = ca/ = c/a
ОПЗ: R1R2c*ed*–/
3. Третье действие: R3 = R2c* = R2*c = c/a*c
ОПЗ: R1R3ed*–/
4. Четвертое действие: R4 = ed* = e*d
ОПЗ: R1R3R4–/
5. Пятое действие: R5 = R3R4– = R3–R4 = c/a*c–e*d
ОПЗ: R1R5/
6. Шестое действие: R6 = R1R5/ = R1/R5=(a+b)/(c/a*c–e*d)
ОПЗ: R6
ОПЗ вычислено и его значением стало значение выражения R6.
Наиболе известным алгоритмом перевода простого алгебраического выражения в ОПЗ является алгоритм Дейкстры (Э́дсгер Ви́бе Де́йкстра, 1930–2002, – выдающийся нидерландский ученый, идеи которого оказали огромное влияние на развитие компьютерной индустрии). Идея алгоритма основывается на использовании стека и анализе приоритета операций и заключается в следующем:
1. Исходная строка просматривается посимвольно, слева направо до достижения конца строки.
2. Если встречается символ операция, то эта операция при определенных условиях помещается в стек (затем при определенных условиях операции выталкиваются в выходную строку).
3. Если встречаются символы операндов, то они из входной строки поступают сразу в выходную строку.
4. Если встречается открывающаяся скобка, то она всегда помещается в стек.
5. Закрывающаяся скобка ни в стек, ни в выходную строку не помещается. Когда она встречается во входной строке, то из стека выталкиваются все символы до первой встречной открывающейся скобки включительно. При этом знаки операций выталкиваются в выходную строку, а открывающаяся скобка просто удаляется из стека.
6. Необходимо использовать следующие приоритеты операций (табл. 17). Чем больше значение приоритета, тем сильнее операция связывает операнды:
Таблица 17.
Приоритеты операций для вычисления ОПЗ
| Операции | ( | + | – | * | / |
| Приоритет |
7. Если во входной строке текущий символ – знак операции, то сравниваются приоритеты операций из строки и верхушки стека.
8. Если приоритет операции из входной строки больше приоритета операции из верхушки стека, то операция из входной строки стека перемещается в стек.
9. В противном случае из стека выталкиваются все операции с приоритетами большими либо равными приоритету операции из входной строки. После чего операция из входной строки помещается в стек.
10. При встрече конца входной строки содержимое стека выталкивается в выходную строку.
Пример 36.Напишем программу перевода входной строки в ОПЗ.
/* Описание стpуктуpы(элемента стека) */
struct st
{
char c;
struct st *next;
};
struct st *push(struct st *, char);
/* Пpототипы функций */
char DEL(struct st **);
int PRIOR(char);
void main(void)
{
// Стек опеpаций пуст
struct st *OPERS = NULL;
char a[80], outstring[80];
int k, point;
do
{
puts("Введите выражение (в конце поставте '=') : ");
fflush(stdin);
// Ввод аpифметического выpажения
gets(a);
k = point = 0;
// Повтоpяем , пока не дойдем до '='
while(a[k] != '\0' && a[k] != '=')
{
if(a[k] == ')') // Если очеpедной символ - ')', то выталкиваем из
// стека в выходную стpоку все знаки опеpаций до
// ближайшей откpывающей скобки
{
while((OPERS->c) != '(')
outstring[point++] = DEL(&OPERS);
DEL(&OPERS); // Удаляем из стека саму откpывающую скобку
}
if(a[k] >= 'a' && a[k] <= 'z') // Если очеpедной символ - буква , то
// пеpеписываем её в выходную стpоку
outstring[point++] = a[k];
if(a[k] == '(') // Если очеpедной символ - '(' , то заталкиваем её
//в стек
OPERS = push(OPERS, '(');
// Если следующий символ - знак опеpации , то:
if(a[k] == '+' || a[k] == '-' || a[k] == '/' || a[k] == '*')
{
if(OPERS == NULL) // если стек пуст записываем в него опеpацию
OPERS = push(OPERS, a[k]);
else // если не пуст
// если пpиоpитет поступившей опеpации больше пpиоpитета опеpации на веpшине стека заталкиваем поступившую опеpацию на стек
if(PRIOR(OPERS->c) < PRIOR(a[k]))
OPERS = push(OPERS, a[k]); //
else // если пpиоpитет меньше пеpеписываем в выходную стpоку все
// опеpации с большим или pавным пpиоpитетом
{
while((OPERS != NULL) && (PRIOR(OPERS->c) >= PRIOR(a[k]))) //
outstring[point++] = DEL(&OPERS);
OPERS = push(OPERS, a[k]); // записываем в стек поступившую
// опеpацию
}
}
k++; // Пеpеход к следующему символу входной стpоки
}
// После pассмотpения всего выpажения пеpеписываем все опеpации из стека в выходную стpоку и печатаем её
while(OPERS != NULL)
outstring[point++] = DEL(&OPERS);
outstring[point] = '\0';
printf("\n%s\n", outstring);
fflush(stdin);
puts("\Повторить (y/n)?");
}
while(getchar() != 'n');
}
/* Функция push записывает на стек (на веpшину котоpого указывает HEAD)
символ a. Возвpащает указатель на новую веpшину стека */
struct st *push(struct st *HEAD, char a)
{
st* PTR = new st; // Выделение памяти
PTR->c = a; // Инициализация созданной веpшины
PTR->next = HEAD; // Подключение её к стеку
return PTR;// PTR - новая веpшина стека
}
/* Функция DEL удаляет символ с веpшины стека.
Возвpащает удаляемый символ. Изменяет указатель на веpшину стека */
char DEL(struct st **HEAD)
{
struct st *PTR;
char a;
if(*HEAD == NULL) return '\0'; // Если стек пуст, возвpащается '\0'
PTR = *HEAD; // в PTR - адpес веpшины стека
a = PTR->c;
*HEAD = PTR->next; // Изменяем адpес веpшины стека
free(PTR); // Освобождение памяти
return a; // Возвpат символа с веpшины стека
}
// Функция PRIOR возвpащает пpиоpитет аpифметической опеpации
int PRIOR(char a)
{
switch(a)
{
case '*':
case '/':
return 3;
case '-':
case '+':
return 2;
case '(':
return 1;
}
}

Приведем пример использования Алгоритма Дейкстры для входной строки (a+b*c)*(a–b)/(d–(a+b*d)). Для удобства отображения стека в таблице «транспонируем» его, т.е. разместим стек в строке, развернув по часовой стрелке на 90 градусов, так чтобы вершина стека располагалась в конце строки справа (табл.18).
В программировании, кроме списков и стека часто используются подобные динамические структуры, программная реализация которых похожа на списки и стек, но дисциплина доступа к ним и набор типовых операций несколько видоизменены, к ним относятся очередь и дек.
Очередью (aнгл. queue) называется структура данных, в которой элементы кладутся в конец, а извлекаются из начала. Таким образом, первым из очереди будет извлечен тот элемент, который будет добавлен раньше других. Говорят, что очередь реализует дисциплину обслуживания FIFO (First In – First Out, первым пришел – первым ушел). Очередь можно рассматривать как однонаправленный список, в котором можно удалять только из начала, а добавлять только в конец. Основные операции над очередью – такие же, что и над стеком: включение, исключение, определение размера, очистка, обход, чтение.
Деком (англ. deque – аббревиатура от double-ended queue, двухсторонняя очередь) называется структура данных, в которую можно удалять и добавлять элементы как в начало, так и в конец. Дек хранится в памяти так же, как и очередь. Таким образом, дек может быть и стеком, и очередью, и комбинацией этих структур. Наиболее часто дек представляется структурой с ограничением на вход или выход: дек с ограниченным входом (только одна позиция доступна для добавления элемента) и дек с ограниченным выходом (только одна позиция доступна для взятия элемента из дека). Стандартные операции над деком: включение элемента справа; включение элемента слева; исключение элемента справа; исключение элемента слева; определение размера; очистка.
На практике также используются модификации приведенных структур, например циклическая очередь, замкнутый или кольцевой список и т.п. В таких структурах, как правло последний элемент замыкается указателем на первый (и наоборот, – первый ссылается на последний, при двухсторонней связи), что позволяет рассматривать структуру как замкнутое кольцо.
Деревья
Дерево – одна из наиболее распространённых структур данных, используемых в программировании. Формально дерево определяется рекурсивно следующим образом: это конечное множество Т, состоящее из одного или более узлов таких, что:
1. Имеется один узел, называемый корнем дерева.
2. Остальные узлы, исключая корень, содержатся в m≥0 попарно непересекающихся множествах Т1, Т2,….Тm, каждое из которых в свою очередь является деревом. При этом деревья Т1, Т2,….Тm называются поддеревьями (потомками) данного корня.
Поддеревья некоторой вершины еще иногда называют кустами, а конечные вершины дерева из которых больше не выходит ни одной связи (т.е. для такого узла m=0), называют листьями.
Наиболее распространены в программировании бинарные (двоичные) деревья, в которых каждый узел может иметь не более двух потомков. Рекурсивное определение бинарного дерева задает его как корень и два бинарных поддерева: левое и правое, – причем любое из них может быть пустым. Бинарные деревья используются как структура данных в том случае, когда в каждой точке процесса должно быть принято одно из двух возможных решений. Например, они применяются для синтаксического анализа, поиска, сортировки, управления базами данных и в других приложениях.
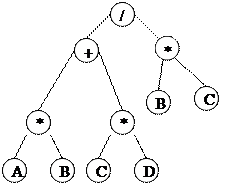
Пример 37. Приведем пример бинарного дерева (рис.44), которое может использоваться для вычисления алгебраического выражения (A*B+C*D)/(B*C), если двигаться от листьев дерева к корню.
 |
|
Бинарные деревья наиболее часто используются в программировании. Это основывается на том факте, что любое дерево может быть приведено к бинарному. Основное правило такого преобразования: левая ветвь каждого узла соединяет его с первым узлом следующего уровня, а правая – с другими узлами следующего уровня (братьями). Рис.45 демонстрирует первый шаг преобразования дерева A к его бинарному представлению. На втором шаге тоже самое делается с поддеревом B и т.д.
 |  | ||
| Рис.45. Шаг преобразования дерева к бинарному |
Бинарное дерево на языке Си может быть описано следующими структурами данных:
struct tree
{
int info; //информационное поле
tree ltree,rtree; //указатели на левое и правое поддерево
}
К бинарным деревьям применяют следующие типовые операции:
1. Создание нового бинарного дерева, состоящего из одного узла с информационным полем .
2. Создание нового левого или правого «сына» (узла) для текущего узла.
3. Чтение информационного содержимого узла.
4. Определение указателя на левое или правое поддерево.
5. Удаление куста или листа дерева.
6. Удаление левого или правого поддерева для узла.
7. Обход дерева.
8. Сравнение деревьев.
9. Соединение деревьев.
Пример 40. Рассмотрим реализацию основных процедур и функции для работы с деревьями.
tree MakeTree(tree node, int x)
{
if(node.value == NULL)
{
tree* p = new tree;
p->value = x;
node = *p;
}
else
{
if((node).value > x) MakeTree(*node.pleft, x);
else MakeTree(*node.pright, x);
}
return node;
}
void SetLeft (tree *p,int x) // создание левого сына для узла с указателем p
{
*p->ltree = NewNode(x);
}
void SetRight(tree *p,int x) // создание правого сына для узла с указателем p
{
*p->rtree = NewNode(x);
}
int GetInfo (tree *p) // чтение значения информационного поля узла p
{
if (p != NULL) return p->info;
else return(0);
}
tree GetLeftTree (tree *p) // выдать значение указателя на левое поддерево
// узла p
{
if (p != NULL) return *p->ltree;
//else return(NULL);
}
tree GetRightTree (tree *p) //выдать значение указателя на правое поддерево
// узла p
{
if (p != NULL) return *p->ltree;
// else return (tree)NULL;
}
void DelLeaf (tree *p) // Удалить в дереве «лист»
{
if (p != NULL) free(p);
}
Рассмотрим более подробно задачу обхода дерева. Обход дерева – это последовательный обход всех узлов дерева. Фактически во время обхода нужно составить список всех узлов дерева. Поскольку дерево по определению является рекурсивной структурой данных, то и обход дерева как правило осуществляется рекурсивно. Существует три способа рекурсивного обхода бинарного дерева: обход с префиксным порядком; обход с инфиксным порядком; обход с суффиксным (или постфиксным) порядком.
Префиксный порядок обхода дерева определяется в виде списка узлов следующим образом:
Если дерево не пусто, то префиксный порядок это:
1. Корень дерева.
2. Узлы левого поддерева в префиксном порядке.
3. Узлы правого поддерева в префиксном порядке.
Например, пусть дано дерево, указанное вна рис. примере 48, тогда префиксный обход дерева это следующая последовательность узлов: /+*AB*CD*BC. Иногда префиксный порядок называют обходом дерева сверху вниз.
Инфиксный порядок обхода дерева определяется в виде списка узлов следующим образом:
Если дерево не пусто, то инфиксный порядок это:
1. Узлы левого поддерева в инфиксном порядке.
2. Корень дерева.
3. Узлы правого поддерева в инфиксном порядке.
Для нашего примера это будет: A*B+C*D/B*C
Суффиксный порядок обхода дерева определяется в виде списка узлов следующим образом:
Если дерево не пусто, то суффиксный порядок это:
1. Узлы левого поддерева в суффиксном порядке.
2. Узлы правого поддерева в суффиксном порядке.
3. Корень дерева.
Для нашего примера это будет: AB*CD*+BC*/. Суффиксный порядок обхода иногда называют обходом дерева снизу вверх.
Заметим, что инфиксный порядок обхода бинарного дерева в нашем примере совпал с самим алгебраическим выражением, только без скобок, суффиксный порядок – совпал с ОПЗ выражения, а результат префиксного обхода является обратным инфиксному, т.е. сначала указывается операция, затем операнды, – именно так записываются функции и процедуры на языке Паскаль. С обходом дерева как правило совмещаются некоторые действия над проходимой вершиной. Например, в случае суффиксного обхода, можно совместить обход с операцией удаления куста дерева.
void PrefixObhod (tree *p)
{
if (p !=NULL) // Если дерево не пусто, то префиксный порядок это:
{
printf ("%d", p->info); //обработка узла, например напечатем его инф.часть
PrefixObhod (p->ltree); // Узлы левого поддерева в префиксном порядке
PrefixObhod (p->rtree); // Узлы правого поддерева в префиксном порядке
}
}
void InfixObhod (tree *p)
{
if (p != NULL) // Если дерево не пусто, то инфиксный порядок это:
{
InfixObhod (p->ltree); // Узлы левого поддерева в инфиксном порядке
printf ("%d", p->info); //обработка узла, например напечатем его инф.часть
InfixObhod (p->rtree); // Узлы правого поддерева в инфиксном порядке
}
}
void DelSubTree (tree *p) //процедура удаление куста p с использованием суффиксного обхода
{
if (p != NULL) // Если дерево не пусто, то суффиксный порядок это:
{
DelSubTree (p->ltree); // Узлы левого поддерева в суффиксном порядке
DelSubTree (p->rtree); // Узлы правого поддерева в суффиксном порядке
free(p); //обработка узла, например удалим узел
}
}
void DelLeftTree (tree *p) //удаление левого поддерева для узла p
{
if (p != NULL)
{
DelSubTree (p->ltree);
p->ltree = NULL;
}
}
void DelRightTree (tree *p) //удаление правого поддерева для узла p
{
if (p != NULL)
{
DelSubTree (p->rtree);
p->ltree = NULL;
}
}
Сравнение деревьев производится путём сравнения информационной части (информационных полей) соответствующих деревьев, начиная с корня. Функция должна сравнивать информационные части узлов дерева, а далее рекурсивно сравнивать левые и правые поддеревья. Фактически функция осуществляет обход дерева сверху вниз. Выходом из рекурсии в данном случае будет сравнение значений указателей (в том числе и пустых). Для равных деревьев одновременно указатели будут обнулены и станут равными. В случае различия, это равенство не пройдет. Если же оба указателя отличны от пустых, т.е. указывают на поддеревья, то сравниваются их информационные части и соответственно левые и правые потомки. Если все эти три сравнения совпадают, то делается заключение о совпадении сравниваемых деревьев.
Напишем функцию, которая будет выдавать истинное значение, если два дерева равны, и ложное значение в противном случае.
bool TreeEqual(tree *p1, tree *p2)
{
if (p1 == p2) return true;
else
if ((p2 != NULL) && (p1 != NULL))
return ((p1->info = p2->info) && TreeEqual(p1->ltree, p2->ltree) &&
TreeEqual(p1->rtree, p2->rtree));
else return false;
}
