Понятие случайных событий и случайных величин

Случайное событие – событие, которое может появиться или не поя­виться в результате данного опыта [2].

Вероятность случайного события (количественная характеристика случайного события) – теоретическая частота событий, около которой имеет тенденцию стабилизироваться действительная частота события при повторении опыта в данных условиях.

Частота случайного события (статистическая вероятность события) – это отношение числа появления данного события к числу всех произве­денных опытов.

Примеры случайных событий, наиболее характерных для теории на­дежности:

а) событие, заключающееся в том, что на интервале времени от 0 до t изделие непрерывно находится в работоспособном состоянии; вероятность такого события в теории надежности обозначается P(t);

б) событие, заключающееся в том, что на интервале времени от 0 до t изделие может перейти в отказовое состояние, вероятность такого события в теории надежности обозначается Q(t);

в) событие, заключающееся в том, что работоспособное к моменту времени t изделие перейдет за время Dt из состояния работоспособного (состояние 1) в состояние отказа (состояние 2), вероятность такого собы­тия определяется по формуле:

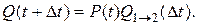(1.1)

Два события называются несовместными в одном опыте, если они не могут появиться совместно.

Вероятность суммы двух несовместных событий, т.е. вероятность того, что из всех возможных событий появится хотя бы одно из них, равна сумме вероятностей этих событий:

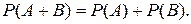(1.2)

Вероятность суммы совместных событий:

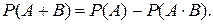(1.3)

Вероятность произведения двух событий – это вероятность того, что событие появятся совместно:

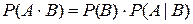, (1.4)

Отсюда вероятность произведения двух независимых событий:

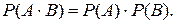(1.5)

Условной вероятностью события А относительно события В называ­ется отношение совместного появления событий А и В к вероятности со­бытия В:

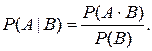(1.6)

Случайная величина – величина, которая в результате опыта может принимать то или другое значение (заранее не известно, какое именно). Она может быть либо дискретной (число отказов за время t, число отка­завших изделий при испытаниях заданного объема), либо непрерывной (время работы изделия до отказа, время восстановления работоспособно­сти).

Исчерпывающее представление о случайной величине дает закон распределения случайной величины – соотношение между значениями случайной величины и их вероятностями.

Существуют законы распределения:

1. Интегральный (функция распределения) – вероятность того, что случайная величина X может принимать значения меньше х:

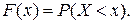(1.7)

Если случайная величина – наработка до отказа t,то вероятность того, что t меньше заданного значения t_з, равна вероятности возникновения отказа на интервале от нуля до t_з. Функция наработки на отказ (функция ненадежности)

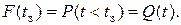(1.8)

Вероятность того, что на интервале времени от 0 до t_з не возникает отказа, определяют по формуле

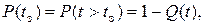(1.9)

где P(t_з) – функция надежности.

2. Дифференциальный (плотность распределения вероятности слу­чайной величины, или, иными словами, плотность распределения случай­ной вели­чины):

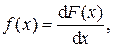(1.10)

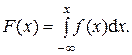(1.11)

Величины, определяющие характер распределения случайной вели­чины, называются параметрами законов распределения.

Математическое ожидание (среднее значение случайной величины)

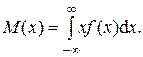(1.12)

Статистическое определение

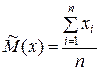. (1.13)

Дисперсия

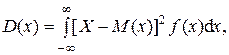(1.14)

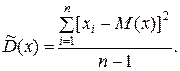(1.15)

Дисперсия среднего значения:

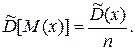(1.16)