Теоретические сведения. Решение таких задач, как планирование расписаний, игровых задач, задач обучения и т

Решение таких задач, как планирование расписаний, игровых задач, задач обучения и т. д. предполагает решение задачи поиска в пространстве состояний. Большинство задач поиска формулируются следующим образом: найти путь из начального состояния (узла или позиции) в целевое состояние (узел или позицию). Задача поиска обычно определяется указанием:

- пространства состояний;

- начального состояния;

- функции генерации соседних для данного состояний;

- целевого условия, т.е. условием, к достиже­нию которого следует стремиться. «Целевые вершины» – это вершины, удовлетворяющие этим условиям. Целевое условие может выполняться для нескольких состояний.

Пространство со­стояний – это граф, вершины которого соответствуют ситуациям, встречающимся в задаче («проблемные си­туации»), а дуги – разрешенным переходам из одних состояний в другие. Решение задачи сводится к поиску пути в этом графе, т.е. в нахождении любой серии перемещений из начального состояния в состояние, удовлетворяющее целевому условию. Например, для задачи поиска кратчайшего пути между двумя городами пространство состояний представляет собой города на карте и его можно представить в виде графа следующим образом:

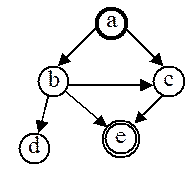
Рис. 7.1. Представление пространства состояний в виде графа

На этом рисунке состояние a является стартовым состоянием, а состояние e – целевым. Решение задачи сводится к нахождению кратчайшего пути из города a в город e.

Процесс ре­шения задачи включает в себя поиск в графе, при этом, как правило, возникает проблема, как обраба­тывать альтернативные пути поиска. Существуют две основные стратегии перебора альтернатив, а именно поиск в глубину и поиск в ширину. Пространство состояний неко­торой задачи определяет «правила игры»: вершины пространства состояний соответствуют ситуациям, а дуги – разрешенным ходам или действиям, или шагам решения задачи. Каждому разрешенному ходу или действию можно приписать его стоимость. В тех случаях, когда каждый ход имеет стои­мость, мы заинтересованы в отыскании решения мини­мальной стоимости. Стоимость решения – это сумма стоимостей дуг, из которых состоит «решающий путь» – путь из стартовой вершины в целевую. Даже если стоимости не заданы, все равно может возникнуть оптимизационная задача: нас может интересовать кратчайшее решение.

Представление пространства состояний

Когда поиск проводится в графе состояний, граф фактически разворачивается в дерево, причем некоторые пути, возможно, дублируются в разных частях этого дерева. Поэтому для простоты все приведенные ниже примеры касаются поиска в дереве. На рисунке 7.2 приведен граф состояний и его представление в виде дерева.

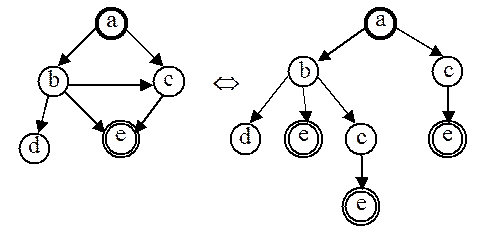
Рис. 7.2. Представление пространства состояний в виде дерева

Для дальнейшего изложения будем использовать дерево состояний, представленное на рисунок 7.3. Для простоты реализации алгоритма поиска такое дерево может быть представлено как список всех возможных путей от его листьев до корня.

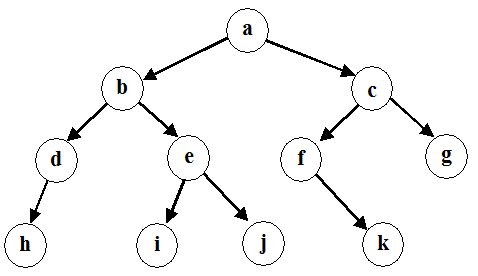
Рис. 7.3. Дерево состояний

Ниже дано представление дерева состояний (рис. 7.3) в виде списка всех возможных путей:

((h d b a)

(i e b a)

(j e b a)

(k f c a)

(g c a))

Алгоритм поиска

В общем, алгоритм поиска в дереве состояний следующий:

1. Создать очередь, содержащую один частичный путь (начальное состояние).

2. Расширить первый в очереди частичный путь. При этом первый путь извлекается из очереди, а для первой вершины этого пути находится множество связанных с ней вершин, т.е. строятся следующие частичные пути. Затем очередь частичных путей обновляется.

3. Если какой-то из частичных путей содержит целевой узел, вывести этот частичный путь.

Существует много различных подходов к проблеме поиска решающего пути (т.е. пути, ведущего из стартовой вершины в целевую) для задач, сформулированных в терминах пространства состояний. К основным относятся две стратегии поиска: поиск в глубину и поиск в ширину.Поиск в глубину и поиск в ширину различаются только способом пополнения очереди частичных путей. Поиск в ширину использует принцип FIFO – старый путь уничтожается и новый добавляется в конец очереди. Поиск в глубину использует принцип LIFO – старый путь уничтожается и новый добавляется в начало очереди.

Поиск в глубину

Под названием «поиск в глубину» понимается порядок рассмотрения альтернатив в пространст­ве состояний. Всегда, когда алгоритму поиска в глубину надлежит выбрать из нескольких вершин ту, в которую следует перейти для продолжения поиска, он предпочитает самую «глубокую» из них. Самая глубокая вершина – это вершина, расположенная дальше других от стартовой вершины. На рисунке 7.4 показано в каком порядке алгоритм поиска в глубину обходит вершины дерева состояний.

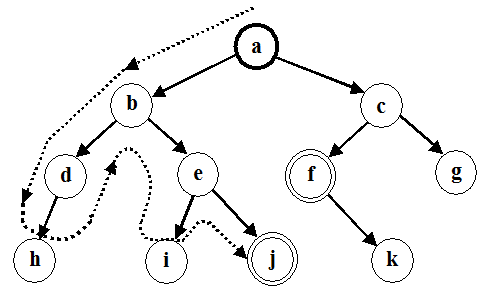
Рис. 7.4. Обход вершин дерева состояний при поиске в глубину

На этом рисунке: а – стартовая вершина, f и j – целевые вершины. Порядок, в котором происходит обход вершин в пространстве состояний при поиске в глубину следующий: а, b, d, h, e, i, j. Вначале алгоритм находит решение: [а, b, е, j]. После возврата обнаружено другое решение: [a, c, f].

Ниже приведена реализация алгоритма поиска в глубину в дереве состояний на языке Паскаль.

Реализацию поиска в глубину выполняет процедура DephtFirstSearch. Процедура в качестве параметров получает указатель на вершину дерева и указатели на начало и конец двунаправленной очереди, в которой размещаются указатели на соответствующие узлы дерева. Двунаправленная очередь выбрана для удобства занесения и удаления элементов в конце очереди.

На первом этапе в очередь заносится указатель на вершину дерева. Для реализации первого поиска процедура DephtFirstSearch вызывает процедуру PBDPPm, которая в качестве параметров получает указатели на вершину дерева и на начало и конец очереди из одного элемента – указатель на вершину дерева. Процедура PBDPPm отыскивает путь от корня дерева к его самому левому листу и помещает этот путь в очередь, которая является результатом первого поиска и возвращается процедурой DephtFirstSearch в вызывающую программу для последующей обработки. Все последующие поиски выполняются по следующей схеме. После очередной обработки очереди вызывается процедура DephtFirstSearch. В качестве параметров она получает указатели на вершину дерева и на начало и конец очереди, являющейся результатом предыдущего поиска. В процедуре очередь обрабатывается следующим образом. В соответствии с описанием пути, содержащимся в очереди, выполняется спуск по дереву. Когда достигается лист дерева, из конца очереди удаляется элемент, соответствующий листу дерева, и начинается откат по пути спуска. В процессе отката возможны следующие случаи:

- если возврат к узлу выполняется из правого поддерева, то из конца очереди удаляется соответствующий этому узлу элемент и откат продолжается;

- если возврат к узлу выполняется из левого поддерева, то выполняется проверка – есть ли у него правый сын;

- если правого сына у узла нет, то из конца очереди удаляется соответствующий этому узлу элемент и откат продолжается;

- если правый сын у узла есть, то откат прекращается. Указатель на правого сына узла передается в процедуру PBDPPm как указатель на вершину поддерева. Процедура отыскивает путь от корня поддерева к его самому левому листу и дописывает соответствующие элементы в конец двунаправленной очереди, которая, является результатом очередного поиска. Результат очередного поиска возвращается процедурой DephtFirstSearch в вызывающую программу.

Ниже приводится полное описание всех необходимых типов данных и вспомогательных процедур.

type TPNode= ^TNode;

TNode = record

Inf: array [1..10] Of Char;

Left, Right: TPNode;

end;

TPointDQueue = ^TDQueue; {Двунаправленный список}

TDQueue = record

PNTree: TPNode;

Next, Prev: TPointQueue;

end;

varRut: TPNode;

BeginQueue,EndQueue: TPointDQueue;

{InsertDQ - процедура занесения элемента в двунаправленную очередь}

procedure InsertDQ(var BegQue, EndQue:TPointDQueue;

NewElm: TPNode);

var WP: TpointDQueue;

Begin

New(WP);

WP^.PNTree := NewElm;

WP^.Next := Nil;

WP^.Prev := Nil;

if EndQue = Nil then

Begin

BegQue := WP; {cлучай первого элемента}

EndQue := WP

End

Else

Begin

EndQue^.Next := WP;

WP^.Prev := EndQue;

EndQue := WP

End

end; {InsertDQ}

{EmptyDQ - функция проверки очереди на пустоту}

functionEmptyDQ(BegQue: TPointDQueue): boolean;

Begin

if BegQue = Nil then Empty: = True

elseEmpty := False

end; {EmptyDQ}

{RemoveDQEnd – процедура удаления последнего элемента
двунаправленной очереди}

procedure RemoveDQEnd(var BegQue,EndQue:
TpointQueue;

PrevEndQue:TpointQueue);

varWP: TpointQueue;

Begin

if Empty(BegQue) = TruethenExit;

{элемент удаляется из конца очереди}

WP := EndQue;

EndQue := EndQue^.Prev;

Dispose(WP);

{если в очереди оставался один (последний) элемент, то его
удаление приводит к пустой очереди, следовательно, BegQue = Nil и
EndQue = Nil}

if EndQue = Nil then BegQue := Nil;

end; {RemoveQEnd}

{PBDPPm – выполняет поиск самого левого из возможных путей от
вершины, переданной как корень дерева. Или иначе, процедура выполняет
поиск пути от корня к самому левому листу дерева}

procedure PBDPPm(PTree: TPNode;

var BegQ, EndQ: TPointQueue);

Begin

{вставка очередного элемента в очередь}

InsertQ (BegQ, EndQ, PTree);

if Ptree^.Left <> Nil then

PBDPPm(PTree^.Left, BegQ, EndQ)

Else

if Ptree^.Right <> Nil then

PBDPPm(PTree^.Right, BegQ, EndQ)

end; {PBDPPm}

{DephtFirstSearch – процедура возвращает указатель на начало
двунаправленной очереди, содержащей указатели на все узлы дерева,
полученные в результате очередного поиска в глубину.}

procedure DephtFirstSearch(var WRoot: TNode;

var BegQ, EndQ: TPointQueue);

var Prev, Curr: TPointQueue;

Begin

{В очередь занесен только один элемент – корень дерева.}

if BegQ = EndQ then

{Поиск первого пути в дереве - пути от корня к самому левому
листу дерева }

PBDPPm(WRoot, BegQ, EndQ)

Else

{В очередь занесено несколько элементов. Поиск пути от корня к
очередному листу дерева}

Begin

Prev := BegQ;

Curr := BegQ^.Next;

if Curr <> Nil then

{Спуск по предыдущему пути до листа дерева. Выполнять
контроль на достижение листа дерева нет
необходимости т.к. такой контроль выполняется
автоматически по концу очереди}

if(WRoot^.Left^.Inf=Curr^.Inf) then

Begin

{Спуск по левой ветви узла}

DephtFirstSearch

(WRoot^.Left, Curr, EndQ);

{Возврат из рекурсии из левого поддерева}

if (WRoot^.Right = Nil) then

{При возврате из левого поддерева, если у
узла нет правого сына, то узел удаляется из
пути поиска}

RemoveQEnd

(BegQ, EndQ, PrevEndQue)

Else

{При возврате из левого поддерева, если у
узла есть правый сын, он становится
корнем поддерева, для которого
определяется путь к его самому левому
листу. Этот путь дописывается в конец
очереди}

PBDPPm

(WRoot^.Right, BegQ, EndQ);

End

Else

Begin

{Спуск по правой ветви узла}

DephtFirstSearch

(WRoot^.Right, Curr, EndQ);

{Возврат из рекурсии из правого поддерева}

RemoveQEnd(BegQ, EndQ,PrevEndQue);

{При возврате из правого поддерева узел
удаляется из пути поиска}

End

Else

{Лист дерева из предыдущего пути поиска автоматически
удаляется из дерева и начинается откат по пути поиска}

RemoveQEnd(BegQ, EndQ, PrevEndQue);

end;

end; {DephtFirstSearch}

Обращение к этим процедурам имеет вид:

Begin

• • •

BeginQueue := Nil;

EndQueue := Nil;

{занесение корня дерева в очередь}

InsertQ(BeginQueue, EndQueue, Rut);

{первый поиск}

DephtFirstSearch(Rut, BeginQueue, EndQueue);

• • •

{очередной поиск}

DephtFirstSearch(Rut, BeginQueue, EndQueue);

end.

В случае приведенного выше примера дерева состояний этот процесс будет развиваться следующим образом:

1. Начинаем с начального множества кандидатов:

[[а]]

2. Порождаем продолжения пути [а]:

[[b,а], [с,а]]

(Обратите внимание, что пути записаны в обратном порядке.)

3. Удаляем первый путь из множества кандидатов и порождаем его продолжения: [[d,b,a], [е,b,а]], а затем добавляем список продолжений в начало очереди кандидатов. Получим:

[[d,b,a], [е,b,а], [с, a]]

4. Удаляем [d,b,a] из очереди кандидатов, а затем добавляем все его продолжения в начало очереди. Получаем:

[[h,d,b,a], [е,b,а], [c,a]]

5. Путь [h,d,b,a] не имеет продолжений. Поэтому просто удаляем его из очереди кандидатов. Затем удаляем путь [е,b,а] из очереди кандидатов и добавляем все его продолжения в начало очереди. Получаем:

[[i,е,b,а], [j,e,b,a], [c,a]]

6. После удаления пути [i,е,b,а] из очереди обнаруживается, что путь [j,e,b,a] содержит целевую вершину. Этот путь выдается в качестве решения.

Поиск в ширину

В противоположность поиску в глубину стратегия поиска в ширину предусматривает переход в первую очередь к вершинам, ближайшим к стартовой вершине. В результате процесс поиска имеет тенденцию разви­ваться более в ширину, чем в глубину, что иллюстрирует рис. 7.5.

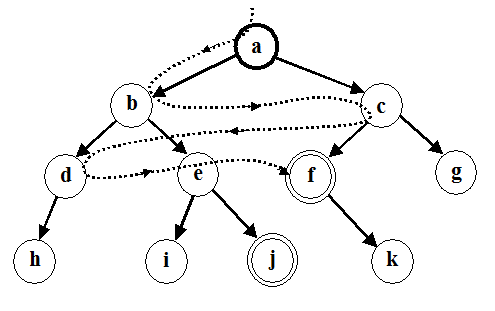
Рис.7.5. Обход вершин дерева состояний при поиске в ширину

На этом рисунке: а – стартовая вершина, f и j – целевые вершины. Применение стратегии поиска в ширину дает следующий порядок обхода вершин: [а, b, с, d, e, i]. Более короткое решение: [a, c, f] найдено раньше, чем более длинное [a, b, e, j].

Поиск в ширину программируется не так легко, как поиск в глубину. Причина состоит в том, что нам приходится сохранять все множество альтерна­тивных вершин-кандидатов, а не только одну верши­ну, как при поиске в глубину. Более того, если мы желаем получить при помощи процесса поиска решаю­щий путь, то одного множества вершин не достаточно. Поэтому надо хранить не множество вершин-кандидатов, а множество путей-кандидатов. В случае спискового представления множества кандидатов само множество будет списком путей, а каждый путь – списком вершин, перечисленных в обратном порядке, т. е. головой списка будет самая последняя из порожденных вершин, а последним элементом списка будет стартовая вершина. Для того, чтобы выполнить поиск в ширину при заданном множестве путей-кандидатов, нужно:

- если голова первого пути является целевой вер­шиной, взять этот путь в качестве решения;

- иначе удалить первый путь из множества кандидатов и породить множество всех возможных продол­жений этого пути на один шаг; множество про­должений добавить в конец множества кандида­тов, а затем выполнить поиск в ширину с по­лученным новым множеством.

Ниже приведена реализация алгоритма поиска в ширину в дереве состояний на языке Паскаль.

Для реализации поиска в ширину корень дерева помещается в очередь и она передается в процедуру. В процедуре очередь обрабатывается следующим образом. Отмечается начало и конец очереди. Для первого элемента очереди – узла дерева, раскрываются его левый и правый сыновья и соответствующие элементы последовательно помещаются в очередь вслед за признаком конца очереди. Первый элемент удаляется из очереди и все повторяется заново до тех пор, пока исходная очередь не будет исчерпана. Таким образом, если на вход процедуры передается очередь из узлов дерева уровня К, то после своего выполнения процедура возвращает очередь из узлов дерева уровня К + 1. Полученная очередь может подвергнуться обработке, после чего выполняется очередное обращение к процедуре и т.д.

Ниже приводится полное описание всех необходимых типов данных и вспомогательных процедур.

type TPNode= ^TNode;

TNode = record

Inf: array [1..10] Of Char;

Left, Right: TPNode;

end;

TPointQueue = ^ TQueue;

TQueue = record

PNTree: TPNode;

Next: TPointQueue;

end;

var Rut: TPNode;

BeginQueue, EndQueue, BeginList: TpointQueue;

{процедура занесения элемента в очередь}

procedure InsertQ(var BegQue, EndQue: TPointQueue;

NewElm: TPNode);

var WP: TpointQueue;

Begin

New (WP);

WP^.PNTree := NewElm;

WP^.Next := Nil;

if EndQue = Nil then

Begin

BegQue := WP; {cлучай первого элемента}

EndQue := WP

End

Else

Begin

EndQue^.Next := WP;

EndQue := WP;

End

end; {InsertQ}

{функция проверки очереди на пустоту}

function EmptyQ(BegQue: TPointQueue): boolean;

Begin

if BegQue = Nil then Empty := True

else Empty := False

end; {EmptyQ}

{RemoveQL - процедура извлекает элемент из очереди, но не удаляет его}

procedure RemoveQL(var BegQue, EndQue, BegQueL:

TPointQueue);

Begin

if Empty (BegQue) = False then

Begin

{элемент удаляется из очереди}

BegQueL := BegQue;

BegQue := BegQue^.Next;

if BegQue = Nil then EndQue:= Nil

{если в очереди оставался один (последний) элемент, то
его удаление приводит к пустой очереди, следовательно,
BegQue = Nil и EndQue = Nil}

End

end; {RemoveQL}

Следующая процедура возвращает указатель на начало очереди, содержащей указатели на все узлы дерева, полученные в результате горизонтального обхода узлов дерева уровня К = 1- N.

procedure BreadthFirstSearch(var BegQ, EndQ:

TPointQueue);

var WP: TPointQueue;

Begin

WP:= EndQ;

Repeat

{элементы дописываются в очередь до тех пор, пока не будут
перебраны все узлы дерева уровня К.}

if BegQ^.PNTree^.Left <> Nil then

{занесение левого потомка узла дерева в очередь.}

InsertQ (BegQ, EndQ, WPB^.PNTree^.Left);

if BegQ^.PNTree^.Right <> Nil then

{занесение правого потомка узла дерева в очередь.}

InsertQ (BegQ, EndQ, WPB^.PNTree^.Right);

{изъятие элемента из очереди и его занесение в список}

RemoveQL(BegQ, EndQ, BegL: TPointQueue);

until (BegQ = WP);

end; {BreadthFirstSearch}

Обращение к этим процедурам имеет вид:

Begin

• • •

BeginQueue := Nil;

EndQueue := Nil;

{занесение корня дерева в очередь}

InsertQ (BeginQueue, EndQueue, Rut);

{первый поиск}

BreadthFirstSearch(BeginQueue, EndQueue);

• • •

{очередной поиск}

BreadthFirstSearch(BeginQueue, EndQueue);

End.

В случае приведенного выше примера дерева процесс поиска в ширину будет развиваться следующим образом:

1. Начинаем с начального множества кандидатов:

[[а]]

2. Порождаем продолжения пути [а]:

[[b,а], [с,а]]

(Обратите внимание, что пути записаны в обратном порядке.)

3. Удаляем первый путь из множества кандидатов и порождаем его продолжения:

[[d,b,a], [е,b,а]]

Добавляем список продолжений в конец списка кандидатов:

[с,a], [d,b,a], [е,b,а]]

4. Удаляем [с, а], а затем добавляем все его продолжения в конец множества кандидатов. Получаем:

[[d,b,a], [е,b,а], [f,c,a], [g,c,a]]

Далее, после того, как пути [d,b,a] и [е,b,а] бу­дут продолжены, измененный список кандидатов при­мет вид:

[[f,c,a],[g,c,a],[h,d,b,a],[i,e,b,a],[j,e,b,a]]

В этот момент обнаруживается путь [f, c, a], содержащий целевую вершину f . Этот путь выдается в качестве решения.

Поиск с предпочтением: эвристический поиск

Поиск в графах при решении задач, как правило, не­возможен без решения проблемы комбинаторной слож­ности, возникающей из-за быстрого роста числа аль­тернатив. Эффективным средством борьбы с этим слу­жит эвристический поиск. Один из путей использования эвристической информации о задаче (т.е. информации, относящейся к решаемой задаче и используемой для управления поиском) – это получение численных эвристических оценок для вершин пространства со­стояний. Оценка вершины указывает нам, насколько данная вершина перспективна с точки зрения дости­жения цели. Идея состоит в том, чтобы всегда про­должать поиск, начиная с наиболее перспективной вершины, выбранной из всего множества кандидатов. Подобно поиску в ширину, поиск с предпочтением начинается со стартовой вер­шины и использует множество путей-кандидатов. В то время, как поиск в ширину всегда выбирает для продолжения самый короткий путь (т.е. переходит в вершины наименьшей глубины), поиск с предпочтением вносит в этот принцип следующее усовершенствова­ние: для каждого кандидата вычисляется оценка и для продолжения выбирается кандидат с наилучшей оценкой. Допустим s – стартовая вершина дерева состояний, а t – целевая. Для каждого узла n, лежащего на пути из s в t, вычисляется оценочная функция f(n). f – это эвристическая оценочная функция, при помощи которой мы получаем для каждой вершины n оценку f(n) «трудности» этой вершины». Тогда наиболее перспективной вершиной-кандидатом следует считать вершину, для которой эта функция принимает минималь­ное значение. Функция f(n) должна быть построена та­ким образом, чтобы давать оценку стоимости опти­мального решающего пути из стартовой вершины s к одной из целевых вершин при условии, что этот путь проходит через вершину n. Оценку f(n) можно представить в виде суммы из двух сла­гаемых (рис. 7.6.): f(n) = g(n) + h(n). Здесь g(n) – оценка оптимального пути из s в n; h(^­n) –- оценка оптимального пути из n в t.

Рис. 7.6. Построение эвристической оценки f(n) стоимости самого дешевого пути из s в t .

Когда в процессе поиска мы попадаем в вершину n, мы оказываемся в следующей ситуации: путь из s в n уже найден, и его стоимость может быть вычис­лена как сумма стоимостей составляющих его дуг (будем предполагать, что для дуг пространства состояний определена функция стоимо­сти с(n, n’) – стоимость перехода из вершины n к вершинe-преемнику n'). Этот путь не обязательно оптимален (возможно, су­ществует более дешевый, еще не найденный путь из s в n), однако стоимость этого пути можно использо­вать в качестве оценки g(n) минимальной стоимости пути из s в n. Что же касается второго слагаемого h(n), то о нем трудно что-либо сказать, поскольку к этому моменту область пространства состояний, лежащая между n и t, еще не «изучена» программой поиска. Поэтому, как правило, о значении h(n) мож­но только строить догадки на основании эвристичес­ких соображений, т.е. на основании тех знаний о конкретной задаче, которыми обладает алгоритм. Поскольку значение h зависит от предметной облас­ти, универсального метода для его вычисления не существует. Будем считать, что тем или иным способом функция h задана, и сосредоточим внимание на деталях алгоритма поиска с предпочтением.

Можно представлять себе поиск с предпочтением следующим образом. Процесс поиска состоит из неко­торого числа конкурирующих между собой подпроцессов, каждый из которых занимается своей альтернативой, т.е. просматривает свое поддерево. У подде­ревьев есть свои поддеревья, их просматривают подпроцессы подпроцессов и т.д. В каждый данный мо­мент среди всех конкурирующих процессов активен только один – тот, который занимается наиболее перспективной к настоящему моменту альтернативой, т.е. альтернативой с наименьшим значением f. Ос­тальные процессы спокойно ждут того момента, когда f-оценки изменятся и в результате какая-нибудь другая альтернатива станет наиболее перспективной. Тогда производится переключение активности на эту альтернативу. Механизм активации-дезактивации про­цессов функционирует следующим образом: процесс, работающий над текущей альтернативой высшего прио­ритета, получает некоторый «бюджет» и остается ак­тивным до тех пор, пока его бюджет не исчерпался. Находясь в активном состоянии, процесс продолжает углублять свое поддерево. Встретив целевую вершину, он выдает соответствующее решение. Величина бюджета, предоставляемого процессу на данный кон­кретный запуск, определяется эвристической оценкой конкурирующей альтернативы, ближайшей к данной.

На рисунке 7.7 показан пример поведения конкури­рующих процессов. Дана карта, а задача состоит в том, чтобы найти кратчайший маршрут из стартового города s в целевой город t . В качестве оценки стоимости остатка маршрута из города n до цели мы будем использовать расстояние по прямой расст(n, t) от n до t.. Таким образом, f(n)= g(n) + h(n) = g(n) + расст(n, t).

Рис. 7.7 Поиск кратчайшего маршрута из s в t

На рисунке 7.7(а) приведена карта со связями между городами. Связи помечены своими длинами; в квадратиках указаны расстояния по прямой до цели t. На рис. 7.7(b) показан порядок, в котором при поиске с предпочтением происходит обход городов. Эвристические оценки основаны на расстояниях по прямой. Пунктирной линией показано переключение активности между альтернативными путями. Эта линия задает тот порядок, в котором вершины принимаются для продолжения пути, а не тот порядок, в котором они порождаются.

Мы можем считать, что в данном примере процесс поиска с предпочтением состоит из двух процессов. Каждый процесс прокладывает свой путь – один из двух альтернативных путей: процесс_1 проходит через a, процесс_2 – через e. Вначале процесс_1 более активен, поскольку значения f вдоль выбранного им пути меньше, чем вдоль второго пути. Когда процесс_1 достигает города c , а процесс_2 все еще находится в e, ситуация меняется:

f(c) = g(c) + h(c) = 6 + 4 = 10

f(e) = g(e) + h(e) = 2 + 7 = 9

Поскольку f(e) < f(c), процесс_2 переходит к f, а процесс_1 ждет. Однако

f(f) = 7 + 4 = 11

f(c) = 10

f(c) < f(f)

Поэтому процесс_2 останавливается, а процессу_1 дается разрешение продолжать движение, но только до d, так как f(d)=12>11. Происходит активация процесса_2, после чего он, уже не прерываясь, доходит до цели t.

Замечания относительно поиска в дереве состояний

- Наиболее распространены две основные стратегии поиска в пространстве состояний: поиск в глубину и поиск в ширину. Поиск в глубину программируется наиболее легко, однако подвержен зацикливаниям. Существуют два простых метода предотвращения зацикливания: ограничить глубину поиска и не допускать дублирования вершин. Поиск в ширину в отличии от поиска в глубину всегда обнаруживает первым самое короткое решение.

- В случае обширных пространств состояний существует опасность комбинаторного взрыва. Обе стратегии плохо приспособлены для борьбы с этой трудностью. В таких случаях необходимо руководствоваться эвристиками.

- Эвристический принцип поиска с предпочтением направляет процесс поиска таким образом, что для продолжения поиска всегда выбирается вершина, наиболее перспективная с точки зрения эвристической оценки.